ВЫ́ПУКЛОЕ ТЕ́ЛО

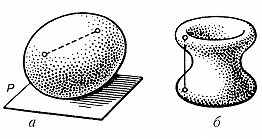
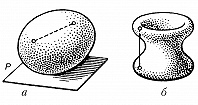
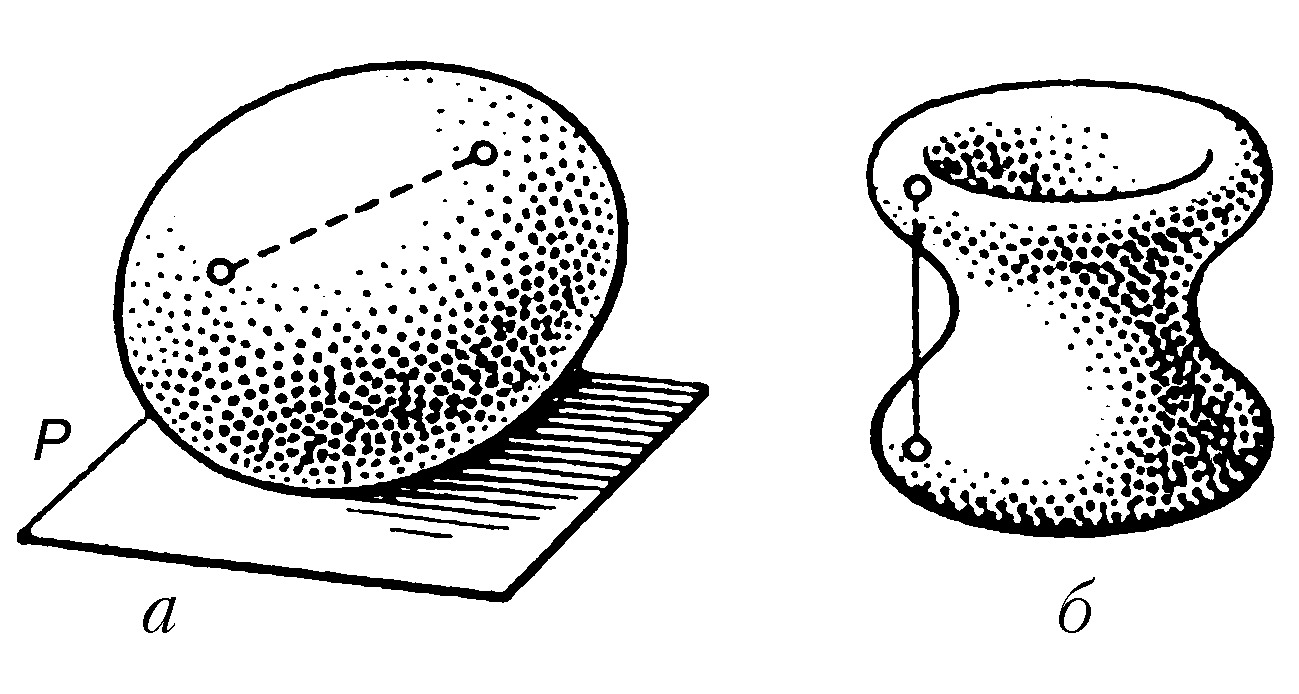
ВЫ́ПУКЛОЕ ТЕ́ЛО, гео­мет­рич. те­ло, об­ла­даю­щее тем свой­ст­вом, что от­ре­зок, со­еди­няю­щий две его лю­бые точ­ки, со­дер­жит­ся в нём це­ли­ком. На рис. a те­ло вы­пук­ло, на рис. б – не вы­пук­ло. При­ме­ра­ми В. т. яв­ля­ют­ся шар, куб, ша­ро­вой сег­мент. Лю­бая связ­ная часть гра­ни­цы (см. Связ­ное мно­же­ст­во) В. т. на­зы­ва­ет­ся вы­пук­лой по­верх­но­стью. Че­рез ка­ж­дую точ­ку гра­ни­цы В. т. про­хо­дит по край­ней ме­ре од­на опор­ная плос­кость, т. е. плос­кость, имею­щая об­щую точ­ку (или от­ре­зок, или часть плос­ко­сти) с гра­ни­цей те­ла, но не рас­се­каю­щая его (плос­кость P на рис. a). В точ­ках, где гра­ни­ца В. т. – глад­кая по­верх­ность, опор­ная плос­кость бу­дет ка­са­тель­ной плос­ко­стью. В тех точ­ках, где глад­кость на­ру­ша­ет­ся (напр., в вер­ши­не ку­ба), су­ще­ст­ву­ет бес­ко­неч­но мно­го опор­ных плос­ко­стей. В. т. мо­гут быть пя­ти ти­пов: ко­неч­ные (гра­ни­ца – замк­ну­тая вы­пук­лая по­верх­ность), бес­ко­неч­ные (гра­ни­ца – од­на бес­ко­неч­ная по­верх­ность; напр., В. т., ог­ра­ни­чен­ное па­ра­бо­лои­дом), бес­ко­неч­ные в обе сто­ро­ны ци­лин­д­ры (гра­ни­ца – замк­ну­тая вы­пук­лая ци­лин­д­рич. по­верх­ность; напр., бес­ко­неч­ный кру­го­вой ци­линдр), слои ме­ж­ду па­ра­ми па­рал­лель­ных плос­ко­стей, всё про­стран­ст­во. Ос­но­вы тео­рии В. т. бы­ли за­ло­же­ны в кон. 19 в. нем. ма­те­ма­ти­ка­ми Г. Брун­ном и Г. Мин­ков­ским. Важ­ней­шие но­вые ре­зуль­та­ты этой тео­рии бы­ли по­лу­че­ны А. Д. Алек­сан­д­ро­вым и А. В. По­го­ре­ло­вым.

Про­стей­ши­ми В. т. яв­ля­ют­ся вы­пук­лые мно­го­гран­ни­ки, т. е. В. т., ог­ра­ни­чен­ные ко­неч­ным чис­лом мно­го­уголь­ни­ков. Для лю­бо­го ко­неч­но­го В. т. мож­но по­стро­ить как угод­но близ­кие к не­му вы­пук­лые мно­го­гран­ни­ки. Это по­зво­ля­ет ре­шать мно­гие за­да­чи о В. т. сле­дую­щим об­ра­зом: за­да­ча ре­ша­ет­ся для вы­пук­лых мно­го­гран­ни­ков, а за­тем с по­мо­щью пре­дель­но­го пе­ре­хо­да со­от­вет­ст­вую­щий ре­зуль­тат пе­ре­но­сит­ся на лю­бое В. т. Так, напр., оп­ре­де­ля­ют­ся пло­ща­ди вы­пук­лых по­верх­но­стей и объ­ё­мы В. т. В ча­ст­но­сти, ус­та­нав­ли­ва­ет­ся, что ес­ли од­но ко­неч­ное В. т. ох­ва­ты­ва­ет дру­гое, то пло­щадь по­верх­но­сти пер­во­го боль­ше пло­ща­ди по­верх­но­сти вто­ро­го. Этот под­ход был пред­ло­жен А. Д. Алек­сан­д­ро­вым (1948) и при­ме­нён для ре­ше­ния разл. за­дач тео­рии вы­пук­лых тел.

Об­щая тео­рия В. т. и вы­пук­лых по­верх­но­стей со­став­ля­ет т. н. гео­мет­рию В. т., вклю­чаю­щую ис­сле­до­ва­ние об­щих свойств В. т. (тео­ре­мы об опор­ных плос­ко­стях, клас­си­фи­ка­ция В. т., при­бли­же­ние мно­го­гран­ни­ка­ми), изу­че­ние экс­тре­маль­ных свойств В. т. (напр., шар сре­ди всех В. т. с за­дан­ным объ­ё­мом име­ет ми­ним. по­верх­ность), тео­ре­мы о су­ще­ст­во­ва­нии и един­ст­вен­но­сти В. т. с за­дан­ны­ми свой­ст­ва­ми, свой­ст­ва разл. клас­сов В. т., а так­же изу­че­ние об­щих свойств вы­пук­лых по­верх­но­стей, тео­ре­мы су­ще­ст­во­ва­ния и един­ст­вен­но­сти для вы­пук­лых по­верх­но­стей.

По­ня­тие В. т. ес­те­ст­вен­но воз­ни­ка­ет и в гео­мет­рии про­странств по­сто­ян­ной кри­виз­ны. Мно­гие пе­ре­чис­лен­ные вы­ше за­да­чи фор­му­ли­ру­ют­ся и ре­ша­ют­ся для В. т. в та­ких про­стран­ст­вах. Ме­то­ды и ре­зуль­та­ты тео­рии В. т. ис­поль­зу­ют­ся в различных раз­де­лах ма­те­ма­ти­ки: в гео­мет­рии, тео­рии чи­сел, ма­те­ма­ти­че­ском ана­ли­зе.