КВА́НТОВЫЙ КОМПЬЮ́ТЕР

КВА́НТОВЫЙ КОМПЬЮ́ТЕР, ком­пь­ю­тер, в ко­то­ром вы­чис­ли­тель­ные опе­ра­ции вы­пол­ня­ют­ся в со­от­вет­ст­вии с за­ко­на­ми кван­то­вой ме­ха­ни­ки. Идея К. к. как уст­рой­ст­ва, по­зво­ляю­ще­го пре­одо­леть труд­но­сти чис­лен­но­го мо­де­ли­ро­ва­ния кван­то­вых сис­тем, бы­ла вы­дви­ну­та Р. Фейн­ма­ном

в нач. 1980-х гг., од­на­ко ши­ро­кую из­вест­ность она при­об­ре­ла по­сле то­го, как в 1994 амер. учё­ный П. Шор пред­ло­жил опи­са­ние кван­то­во­го ал­го­рит­ма, по­зво­ляю­ще­го осу­ще­ст­в­лять фак­то­ри­за­цию (раз­ло­же­ние на мно­жи­те­ли) боль­ших на­ту­раль­ных чи­сел ($n$), ис­поль­зуя мень­шее (по чис­лу зна­ков фак­то­ри­зуе­мо­го чис­ла) ко­ли­че­ст­во эле­мен­тар­ных опе­ра­ций, чем лю­бой из из­вест­ных клас­сич. ал­го­рит­мов (кван­то­вый ал­го­ритм фак­то­ри­за­ции тре­бу­ет по­ли­но­ми­аль­но­го чис­ла – $n^3$ опе­ра­ций). Ал­го­ритм Шо­ра впер­вые про­де­мон­ст­ри­ро­вал сле­дую­щий фе­но­мен – класс слож­но­сти за­да­чи из­ме­ня­ет­ся в за­ви­си­мо­сти от то­го, на ка­ких фи­зич. прин­ци­пах стро­ит­ся вы­чис­лит. про­цесс. По­сколь­ку пред­по­ло­же­ние о прак­тич. не­воз­мож­но­сти фак­то­ри­за­ции большо­го на­ту­раль­но­го чис­ла ле­жит в ос­но­ве не­ко­то­рых совр. ме­то­дов за­щи­ты ин­фор­ма­ции (т. н. сис­тем с от­кры­тым клю­чом), ал­го­ритм, пред­ло­жен­ный Шо­ром, при­вёл к но­вым ис­сле­до­ва­ни­ям в об­лас­ти раз­ра­бот­ки кван­то­вых ком­пь­ю­те­ров.

Ба­зо­вым эле­мен­том К. к. (но­си­те­лем ин­фор­ма­ции) яв­ля­ет­ся кван­то­вый бит – ку­бит (q-бит). В ка­че­ст­ве ку­би­та мо­жет быть вы­бра­на лю­бая кван­то­вая сис­те­ма с дву­мя со­стоя­ния­ми, ха­рак­те­ри­зуе­мы­ми ор­то­нор­ми­ро­ван­ны­ми вол­но­вы­ми функ­ци­я­ми $|\phi_0\rangle$ и $|\phi_1\rangle$, напр. ядер­ный (или элек­трон­ный) спин, ко­то­рый в по­сто­ян­ном внеш­нем маг­нит­ном по­ле име­ет два уров­ня энер­гии, со­от­вет­ст­вую­щих на­прав­ле­ни­ям спи­на вдоль и про­тив по­ля. Эво­лю­ция со­стоя­ний кван­то­вых сис­тем про­ис­хо­дит со­глас­но урав­не­нию Шрё­динге­ра. Кван­то­вая сис­те­ма мо­жет быть мак­ро­ско­пи­че­ской (сверх­про­вод­ни­ки, сверх­те­ку­чие жид­ко­сти, бо­зе-газ), отд. атом­ной час­ти­цей или ко­ле­ба­тель­ной мо­дой. Все эти сис­те­мы мо­гут быть ис­поль­зо­ва­ны в ка­че­ст­ве ку­би­та. Ку­бит функ­цио­ни­ру­ет од­но­вре­мен­но в аб­ст­ракт­ном ма­те­ма­тическом век­тор­ном гиль­бер­то­вом про­стран­ст­ве и в обыч­ном трёх­мер­ном евк­ли­до­вом про­стран­ст­ве (см. Кван­то­вая тео­рия ин­фор­ма­ции

).

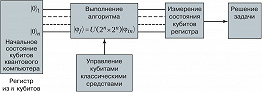
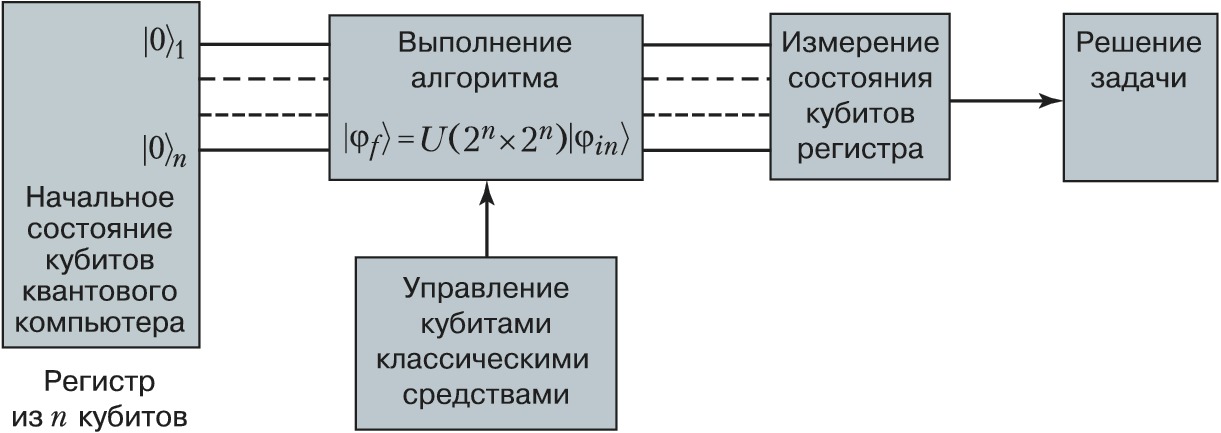
К. к. пред­став­ля­ет со­бой ре­гистр из $n$ ку­би­тов, управ­ляе­мых внеш­ни­ми (клас­сич.) по­ля­ми. Ре­гистр встро­ен в клас­сич. ок­ру­же­ние, со­стоя­щее из управ­ляю­ще­го клас­сич. ком­пь­ю­те­ра, ге­не­ра­то­ров им­пульс­ных по­лей (управ­ляю­щих эво­лю­ци­ей ку­би­тов) и средств из­ме­ре­ния со­стоя­ний ку­би­тов (рис.).

Век­тор со­стоя­ния $|\phi \rangle$ кван­то­во­го ре­гист­ра из $n$ ку­би­тов мож­но раз­ло­жить по $2^n$ ба­зис­ным со­стоя­ни­ям ре­ги­ст­ра (су­пер­по­зи­ция $|\phi \rangle$ бу­дет со­дер­жать $2^n$ сла­гае­мых). Это оз­на­ча­ет, что ог­ра­ни­чен­ный фи­зич. ре­сурс, со­стоя­щий, напр., из $n=10^3$ ку­би­тов, соз­да­ёт ог­ром­ный $2^{1000} \approx 10^{300}$ ма­те­ма­тич. ин­фор­мац. ре­сурс в фор­ме сла­гае­мых су­пер­по­зи­ци­он­но­го со­стоя­ния и ста­но­вит­ся не­дос­туп­ным для са­мых бы­ст­рых клас­сич. ком­пь­ю­те­ров (совр. су­пер­ком­пь­ю­тер вы­пол­ня­ет 10¹⁵ опе­ра­ций в cе­кун­ду, т. е. 10²³ опе­ра­ций в год). Имен­но из это­го об­стоя­тель­ст­ва вы­те­ка­ет пре­иму­ще­ст­во К. к. над клас­си­че­ским. След­ст­ви­ем прин­ци­па су­пер­по­зи­ции яв­ля­ет­ся $2^n$-крат­ный па­рал­ле­лизм вы­чис­ле­ний, т. е. из­ме­не­ние со­стоя­ния толь­ко од­но­го ку­би­та пе­ре­страи­ва­ет всю су­пер­по­зи­цию (ам­пли­ту­ды $2^n$ ба­зисных со­стоя­ний). Вы­чис­лит. про­цесс но­сит ха­рак­тер ин­тер­фе­рен­ции, т. к. ам­пли­ту­ды ба­зис­ных со­стоя­ний яв­ля­ют­ся ком­плекс­ны­ми чис­ла­ми. К. к. мож­но рас­смат­ри­вать как слож­ное ин­тер­фе­рен­ци­он­ное уст­рой­ст­во, в ко­то­ром ин­тер­фе­рен­ция со­стоя­ний

соз­да­ёт вы­чис­лит. мощь ком­пь­ю­те­ра.

Про­цесс вы­чис­ле­ний на К. к. в гиль­бер­то­вом про­стран­ст­ве опи­сы­ва­ет­ся как пре­об­ра­зо­ва­ние век­то­ра на­чаль­но­го со­стоя­ния $|\phi_{in}\rangle$ кван­то­во­го ре­ги­ст­ра в ко­неч­ный век­тор $|\phi_f\rangle$ пу­тём ум­но­же­ния век­то­ра $|\phi_{in}\rangle$ на уни­тар­ную мат­ри­цу $U$ размер­но­стью $2^n \times 2^n$ (в ко­то­рой за­клю­че­ны фор­му­ли­ров­ка за­да­чи и ал­го­ритм её ре­ше­ния): $|\phi_f\rangle=U(2^n \times 2^n)|\phi_{in}\rangle$. Для ре­ше­ния за­да­чи на К. к. тре­бу­ет­ся из­го­то­вить не­об­хо­ди­мое чис­ло ку­би­тов, при­вес­ти их в на­чаль­ное со­стоя­ние $|0\rangle$, т. е. ини­циа­ли­зи­ро­вать их (напр., ох­ла­ж­де­ни­ем ре­ги­ст­ра до сверх­низ­ких темп-р), осу­ще­ст­вить управ­ле­ние их кван­то­вой эво­лю­ци­ей, т. е. вы­пол­нить пре­об­ра­зо­ва­ние $U|\phi_{in}\rangle$. Клас­сич. ин­фор­ма­ция о ре­ше­нии за­да­чи со­дер­жит­ся в ко­неч­ном век­то­ре со­стоя­ния $|\phi_f\rangle$; она по­лу­ча­ет­ся из­ме­ре­ни­ем со­стоя­ния ку­би­тов в ба­зи­се $|0\rangle$, $|1\rangle$. Фи­зич. реа­ли­за­ция из­ме­ре­ния со­стоя­ния отд. ку­би­та со­пря­же­на с ре­ше­ни­ем весь­ма слож­ных тех­но­ло­гич. про­блем, по­сколь­ку не­об­хо­ди­мо про­из­во­дить из­ме­ре­ния со­стоя­ний отд. атом­ной час­ти­цы: со­стоя­ния спи­на элек­тро­на или яд­ра ато­ма, со­стоя­ния ор­би­таль­но­го дви­же­ния элек­тро­на в ато­ме или кван­то­вой точ­ке. По су­ще­ст­ву, для ка­ж­дой реа­ли­за­ции ку­би­та тре­бу­ет­ся раз­ра­бот­ка со­от­вет­ст­вую­ще­го фи­зич. ме­то­да из­ме­ре­ния его со­стоя­ния. Же­ла­тель­но, что­бы дли­тель­ность из­ме­ре­ния бы­ла со­пос­та­ви­мой с дли­тель­но­стью кван­то­вых опе­ра­ций. Про­бле­ма из­ме­ре­ния со­стоя­ния отд. ку­би­тов – од­на из са­мых труд­ных на пу­ти реа­ли­за­ции К. к. Ис­ход кван­то­во­го из­ме­ре­ния яв­ля­ет­ся ве­ро­ят­но­ст­ным (т. е. К. к. – циф­ро­вой ве­ро­ят­но­ст­ный ком­пь­ю­тер), по­это­му для по­лу­че­ния дос­то­вер­но­го ре­зуль­та­та не­об­хо­ди­мо мно­го­крат­ное по­вто­ре­ние ал­го­рит­ма. По спо­со­бу управ­ле­ния К. к. яв­ля­ет­ся ана­ло­го­вым ком­пь­ю­те­ром. По со­вре­мен­ным оцен­кам, па­ра­мет­ры управ­ляю­щих ком­пь­ю­те­ром сиг­на­лов долж­ны кон­тро­ли­ро­вать­ся с точ­но­стью 10^–4–10^–5.

Экс­пе­рим. ис­сле­до­ва­ния по соз­да­нию ку­би­тов и К. к. ве­дут­ся по не­сколь­ким на­прав­ле­ни­ям. Ме­тод ЯМР в жид­ко­с­тях при ком­нат­ной темп-ре по­зво­лил про­де­мон­ст­ри­ро­вать вы­пол­не­ние осн. кван­то­вых ал­го­рит­мов и ме­то­дов кор­рек­ции оши­бок в К. к., со­стоя­щих из се­ми (и ме­нее) ку­би­тов. Од­на­ко по­сле ус­та­нов­ле­ния фак­та, что чис­ло ку­би­тов в дан­ном К. к. ог­ра­ни­че­нно (не бо­лее 10–20), ин­те­рес к раз­ви­тию это­го на­прав­ле­ния не­сколь­ко ос­лаб.

Боль­шое чис­ло экс­пе­ри­мен­тов по реа­ли­за­ции кван­то­вых вы­чис­лит. опе­ра­ций вы­пол­не­но на ио­нах в од­но­мер­ном ион­ном кри­стал­ле в т. н. ло­вуш­ке Пау­ля (удер­жа­ние ио­на в ко­то­рой обес­пе­чи­ва­ет­ся толь­ко элек­трич. си­ла­ми). Од­на­ко и здесь об­на­ру­же­ны серь­ёз­ные пре­пят­ст­вия по уве­ли­че­нию чис­ла ку­би­тов (ио­нов в од­но­мер­ном кри­стал­ле) из-за не­ус­той­чи­во­сти од­но­мер­но­го ион­но­го кри­стал­ла. Эту про­бле­му мож­но пре­одо­леть, напр., ис­поль­зуя ан­самбль мн. ло­ву­шек. В этом слу­чае не­об­хо­ди­мы ме­то­ды бы­ст­рой транс­пор­ти­ров­ки ио­нов из од­ной ло­вуш­ки в дру­гую, напр., с по­мо­щью управ­ляе­мых на­пря­же­ний на элек­тро­дах ло­вуш­ки.

Сход­ная с ион­ны­ми кри­стал­ла­ми ар­хи­тек­ту­ра К. к. мо­жет быть осу­ще­ст­в­ле­на в по­лу­про­вод­ни­ко­вом кри­стал­ле ²⁸Si (ядер­ный спин I = 0), в ко­то­ром вве­дён­ные ато­мы ³¹P (ку­би­ты) рас­по­ло­же­ны в ли­ней­ной це­поч­ке (мо­дель Кей­на). Ку­би­том слу­жит ядер­ный (I = ¹/₂) или элек­трон­ный (S = ¹/₂) спин ато­ма ³¹P. Чис­ло ку­би­тов в та­кой ар­хи­тек­ту­ре не ог­ра­ни­че­но. Од­ной из осн. про­блем дан­ной реа­ли­за­ции К. к. яв­ля­ет­ся из­ме­ре­ние со­стоя­ния оди­ноч­но­го спи­но­во­го ку­би­та. Про­бле­ма из­ме­ре­ния ку­би­та об­лег­ча­ет­ся, ес­ли при­бег­нуть к ан­самб­ле­во­му ва­ри­ан­ту ку­би­та (т. е. ку­би­ту, со­стоя­ще­му из ан­самб­ля ато­мов 31 P).

Ве­дёт­ся ак­тив­ная экс­пе­рим. ра­бо­та по соз­да­нию ку­би­тов на элек­тро­нах в по­лу­про­вод­ни­ко­вых кван­то­вых точ­ках, а так­же на сверх­про­вод­ни­ко­вых ме­зо­струк­ту­рах (т. е. струк­ту­рах суб­мик­рон­ных раз­ме­ров). В этих реа­ли­за­ци­ях чи­пы с ку­би­та­ми ста­но­вят­ся схо­жи с чи­па­ми клас­сич. ком­пь­ю­те­ров на тран­зи­сто­рах.

При­ме­не­ние К. к. до­пол­нит совр. вы­чис­лит. тех­ни­ку, по­сколь­ку их ис­поль­зо­ва­ние оп­рав­дан­но лишь в тех слу­ча­ях, ко­гда они да­ют экс­по­нен­ци­аль­ное ус­ко­ре­ние ре­ше­ния за­да­чи, за­ме­няя не­эф­фек­тив­ные клас­сич. ал­го­рит­мы эф­фек­тив­ны­ми кван­то­вы­ми.