КВАНТИ́ЛЬ

КВАНТИ́ЛЬ, чи­сло­вая ха­рак­те­ри­сти­ка слу­чай­ной ве­ли­чи­ны $X$ и со­от­вет­ст­вую­щей функ­ции рас­пре­де­ле­ния $F(x)=P(X \lt x)$, $- \infty \lt x \lt \infty$; К. по­ряд­ка $p$, $0 \lt p \lt 1$, – чис­ло $K_p$ та­кое, что $F(K_p) \leq p$ и $F(K_p+0) \geq p$, где $F(K_p)+0=\displaystyle\lim_{\varepsilon>0, \varepsilon \to 0} f(K_p+ \varepsilon).$ К. лю­бо­го по­ряд­ка $p$ ли­бо един­ст­вен­на, ли­бо зна­че­ния $K_p$ за­пол­ня­ют не­ко­то­рый от­ре­зок дей­ст­ви­тель­ной оси. Ес­ли $F(x)$ – стро­го мо­но­тон­ная функ­ция, то К. лю­бо­го по­ряд­ка един­ст­вен­на.

К. $K_{1/2}$ на­зы­ва­ет­ся ме­диа­ной слу­чай­ной ве­ли­чи­ны $X$. В ма­те­ма­тич. ста­ти­сти­ке ис­поль­зу­ет­ся по­ня­тие вы­бо­роч­ной ме­диа­ны (см. Ва­риа­ци­он­ный ряд). К. $K_{m/n}$, где $m=1, \dots, n-1, n=2,3, \dots,$ да­ют в слу­чае их един­ст­вен­но­сти тем луч­шее пред­став­ле­ние о ви­де функ­ции $F(x)$, чем боль­ше чис­ло $n$. При $n=4$ (и $m=1$, $m=3$) К. $K_{m/n}$ на­зы­ва­ют­ся квар­ти­ля­ми, при $n=10$ – де­ци­ля­ми, при $n=100$ – пер­цен­ти­ля­ми.

Ве­ли­чи­ны $(K_{3/4}- K_{1/4})/2$ и $K_{9/10}- K_{1/10}$ ино­гда ис­поль­зу­ют­ся в ка­че­ст­ве ха­рак­те­ри­стик рас­сея­ния рас­пре­де­ле­ния и на­зы­ва­ют­ся со­от­вет­ст­вен­но се­ми­ин­тер­квар­тиль­ной ши­ро­той и ин­тер­де­циль­ной ши­ро­той.

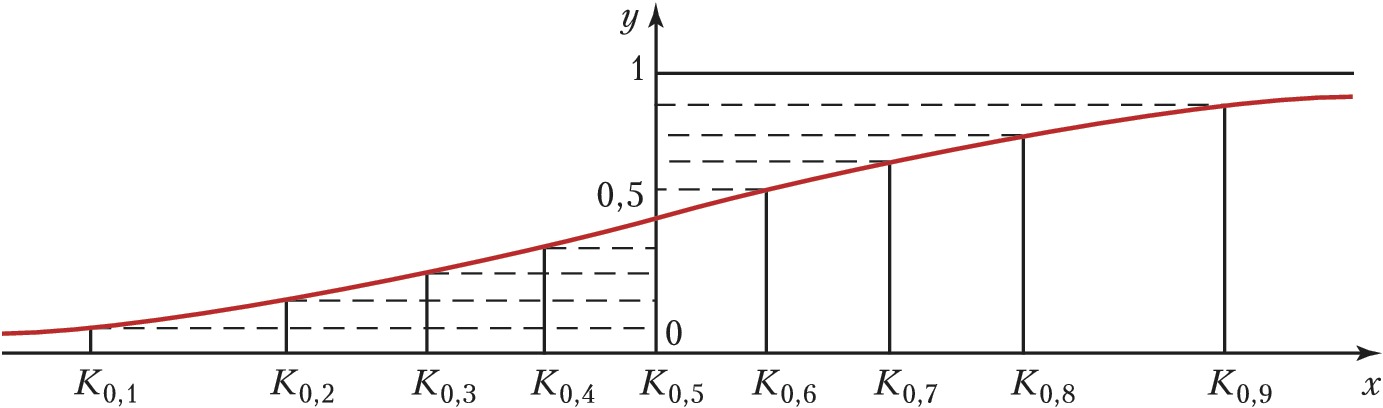
Зна­ние К. для дос­та­точ­но пред­ста­ви­тель­но­го мно­же­ст­ва зна­че­ний $p$, $0 \lt p \lt 1$, по­зво­ля­ет по­лу­чить пред­став­ле­ние о ви­де функ­ции рас­пре­де­ле­ния. В ча­ст­но­сти, гра­фик функ­ции рас­пре­де­ле­ния стан­дарт­но­го нор­маль­но­го за­ко­на $$Ф(x)= \frac {1}{\sqrt{2\pi}}\int^x_{-\infty}e^{-z^2/2}dz$$мож­но по­лу­чить (рис.) по де­ци­лям K0,1 = –1,28, K0,2 = –0,84, K0,3 = –0,52, K0,4 = –0,25, K0,5 =0, K0,6 = 0,25, K0,7 = 0,52, K0,8 = 0,84, K0,9 = 1,28. Квар­ти­ли нор­маль­но­го рас­пре­де­ле­ния $Ф(x)$ суть K1/4 = –0,67, K3/4 = 0,67.