ИСЧЕ́РПЫВАНИЯ МЕ́ТОД

ИСЧЕ́РПЫВАНИЯ МЕ́ТОД, ме­тод до­ка­за­тель­ст­ва, при­ме­няв­ший­ся ма­те­ма­ти­ка­ми древ­но­сти при оп­ре­де­ле­нии пло­ща­дей и объ­ё­мов.

Одна из типичных схем доказательств при помощи И. м. может быть изложена в совр. обозначениях следующим образом. Для определения значения неизвестной величины $A$ можно построить некоторую последовательность величин $C_1, C_2, ..., C_n, ...$ такую, что  $$C_n < A \qquad (1)$$ для всех $n$, и указать величину $B$ такую, что  $$C_n < B \qquad (2)$$ для всех $n$. При этом последовательность $C_1, C_2, ..., C_n, ...$ и величина $B$ долж­ны быть та­ки­ми, что спра­вед­ли­вы не­ра­вен­ст­ва  $$K(A - C_n) < D \qquad (3)$$   $$K(B - C_n) < D \qquad (4)$$  при лю­бом це­лом $K$ для дос­та­точ­но боль­ших $n$, где $D$ – по­сто­ян­ная ве­ли­чи­на. В этом слу­чае $A = B$.

С совр. точ­ки зре­ния для пе­ре­хо­да от не­ра­венств (3) и (4) к ра­вен­ст­ву $A = B$ дос­та­точ­но за­ме­тить, что в си­лу ус­ло­вий (1) – (4) $$\lim_{n \to \infty} (A - C_n) = 0, \lim_{n \to \infty} (B - C_n) = 0,$$ $$A = \lim_{n \to \infty} C_n = B.$$

Ма­те­ма­ти­ки древ­но­сти, не рас­по­ла­гав­шие тео­ри­ей пре­де­лов

, об­ра­ща­лись к до­ка­за­тель­ст­ву от про­тив­но­го и до­ка­зы­вали не­воз­мож­ность ка­ж­до­го из не­ра­венств $A < B$, $B < A$. Что­бы оп­ро­верг­нуть пер­вое из них, при по­мо­щи ак­сио­мы Ев­док­са – Ар­хи­ме­да (она со­сто­ит в том, что для лю­бых по­ло­жи­тель­ных ве­ли­чин $a$ и $b$ та­ких, что $a < b$, су­ще­ст­ву­ет це­лое чис­ло $m$ та­кое, что $ma>b$) ус­та­нав­ли­ва­ли, что для $R = B - A$ су­ще­ст­ву­ет та­кое $K$, что $KR > D$, и в си­лу ус­ло­вия (1) по­лу­ча­ли не­ра­вен­ст­ва $$K(B - C_n) > K(B - A) > D,$$  что про­ти­во­ре­чит (4). Ана­ло­гич­но оп­ро­вер­га­лось др. пред­по­ло­же­ние и ос­та­ва­лось толь­ко при­нять ра­вен­ст­во $A = B$.

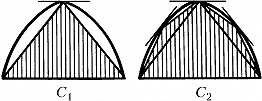
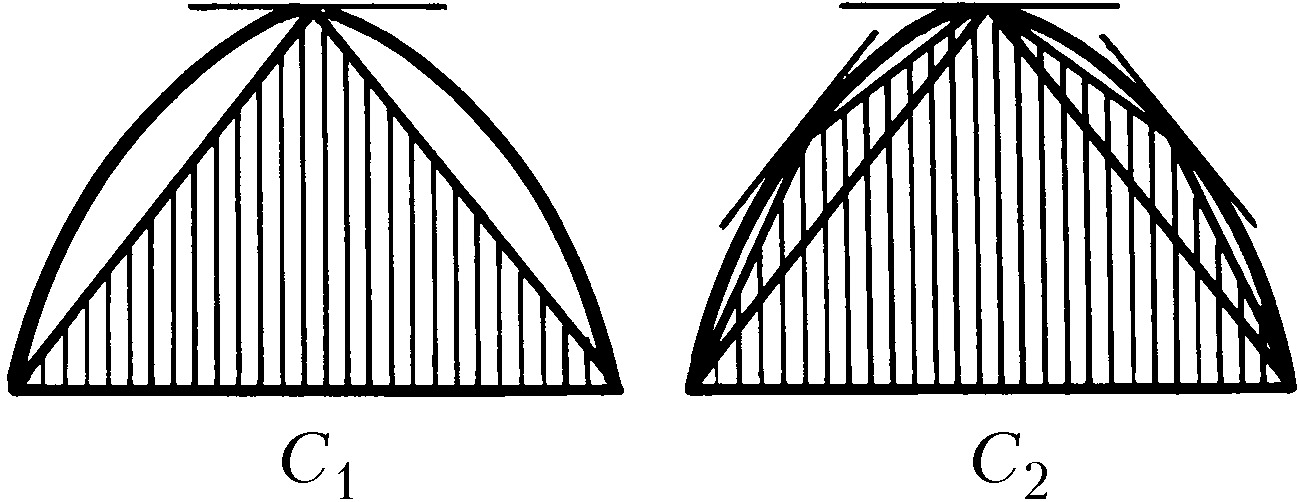
Вве­де­ние И. м. вме­сте с ле­жа­щей в его ос­но­ве ак­сио­мой при­пи­сы­ва­ет­ся Ев­док­су Книд­ско­му

. Этим ме­то­дом ши­ро­ко поль­зо­вал­ся Евк­лид

 >>

, и с осо­бен­ным ис­кус­ст­вом и раз­но­об­ра­зи­ем – Ар­хи­мед

 >>

. Напр., для оп­ре­де­ле­ния пло­ща­ди сег­мен­та, заключённого между па­ра­бо­лой и пересекающей её прямой (рис.), Ар­хи­мед стро­ил пло­ща­ди $C_1, C_2, ..., C_n, ...,$ «ис­чер­пы­ваю­щие» при их по­сте­пен­ном на­рас­та­нии эту пло­щадь. При этом $$C_2 = C_1 + \frac14C_1,$$ $$C_3 = C_1 + \frac14C_1 + \frac{1}{16}C_1,$$ $$C_n = C_1 + \frac14C_1 + ... + \frac{1} {4^{n - 1}}C_1, ...$$ Вме­сто то­го что­бы при­бег­нуть к пре­дель­но­му пе­ре­хо­ду $$A = \lim_{n \to \infty} C_n = \left(1 + \frac{1}{4} + \frac{1}{16} + ...\right)C_1 = \frac{4}{3}C_1,$$  Ар­хи­мед с по­мо­щью гео­мет­рич. со­об­ра­же­ний до­ка­зал, что при лю­бом $n$ спра­вед­ли­во не­ра­вен­ст­во $A - C_n < C_1 / 4^{n - 1},$ для ве­ли­чи­ны $B = 4C_1/3$ ус­та­но­вил, что $$B - C_n = \frac{1}{3 \cdot 4^{n - 1}}C_1,$$ и, сле­дуя из­ло­жен­но­му вы­ше, до­ка­зал, что $A = B = 4C_1/3$.