ДЛИНА́
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
ДЛИНА́, числовая характеристика протяжённости линии. Д. отрезка прямой – расстояние между его концами, измеренное с помощью к.-л. отрезка, принятого за единицу длины. Д. ломаной – сумма Д. её звеньев. Д. простой или жордановой дуги (см. Жордана кривая) – предел Д. вписанных в эту дугу ломаных, когда число звеньев неограниченно увеличивается и максимум Д. звеньев стремится к нулю. Д. непрерывной кривой, состоящей из конечного числа простых дуг, равна сумме Д. этих дуг. Напр., Д. окружности может быть получена как предел периметров правильных вписанных (или описанных) многоугольников при неограниченном удвоении числа их сторон и равна $2πR$, где $R$ – радиус окружности. Всякая непрерывная кривая имеет Д. – конечную или бесконечную. Если её Д. конечна, то кривая называется спрямляемой.
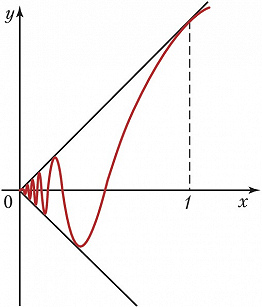
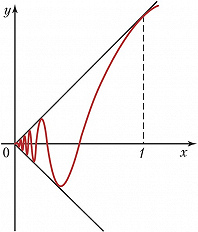
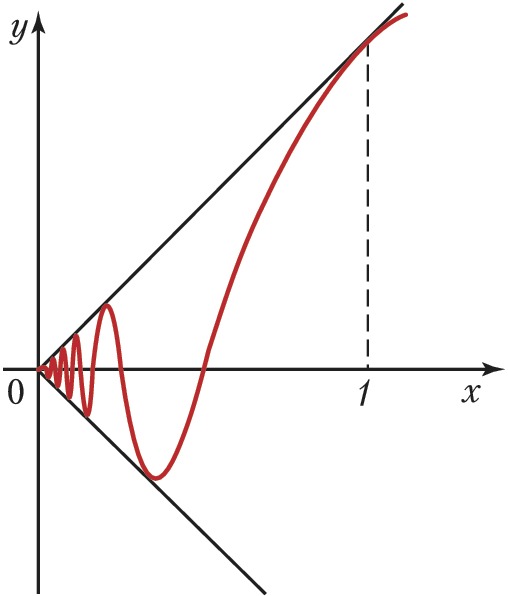
График функции $f(x)=x\sin \frac{\pi}{2x}$ при $0 (рис.) даёт пример неспрямляемой кривой, её Д. бесконечна, т. к. Д. вписанных ломаных неограниченно растут, когда Д. звеньев стремятся к нулю. Д. плоской кривой, заданной в прямоугольных координатах уравнением $y=f(x), a⩽x⩽b$, в случае когда $f(x)$ имеет непрерывную производную $f'(x)$, выражается интегралом $$s=\int_a^b\sqrt{1+(f'(x))^2dx}.$$ Если кривая задана в параметрич. форме $x=x(t), y=y(t), t_1⩽t⩽t_2$, то её Д. равна $$s=\int_{t_1}^{t_2}\sqrt{(x'(t))^2+(y'(t))^2}dt.$$
Д. спрямляемой кривой не зависит от параметризации. Д. пространственной кривой, заданной в параметрич. форме $x=x(t), y=y(t), z=z(t), t_1⩽t⩽t_2,$ выражается формулой $$s=\int_{t_1}^{t_2}\sqrt{(x'(t))^2+(y'(t))^2+(z'(t))^2}dt.$$
Использование предельного перехода для вычисления Д. кривых при помощи Д. ломаных было известно математикам древности. Однако понятие Д. кривой не определялось, т. к. представлялось, по-видимому, одним из первоначальных математич. понятий. Необходимость строгого определения Д. кривой стала ясна в 1-й пол. 19 в. Строгий подход к понятию Д. кривой предложен М. Э. К. Жорданом в 1880-х гг. В дифференциальной геометрии определяется также Д. кривой на поверхности или в произвольном римановом пространстве.
Д. в математике, как правило, – безразмерная величина. Единица Д. в Международной системе единиц – метр.