ЛАНДА́У ЗАТУХА́НИЕ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
ЛАНДА́У ЗАТУХА́НИЕ, затухание колебаний и волн в плазме, которое происходит в отсутствие столкновений между частицами и обусловлено резонансным поглощением энергии волны частицами. Открыто Л. Д. Ландау в 1946. Л. з. возможно для волн малой амплитуды (линейное затухание) и волн конечной амплитуды (нелинейное затухание), в отсутствие магнитного поля (затухание ленгмюровских и ионно-звуковых волн) и при его наличии (циклотронные резонансы).
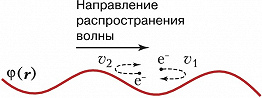
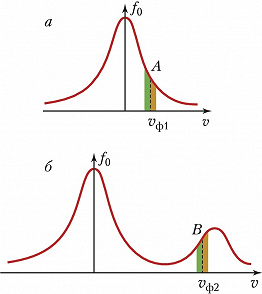
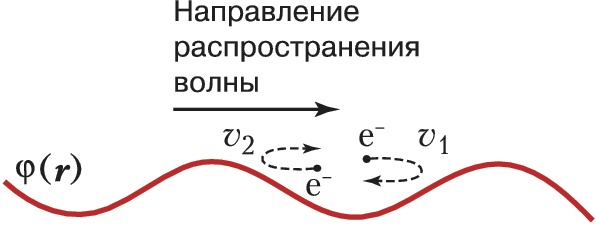
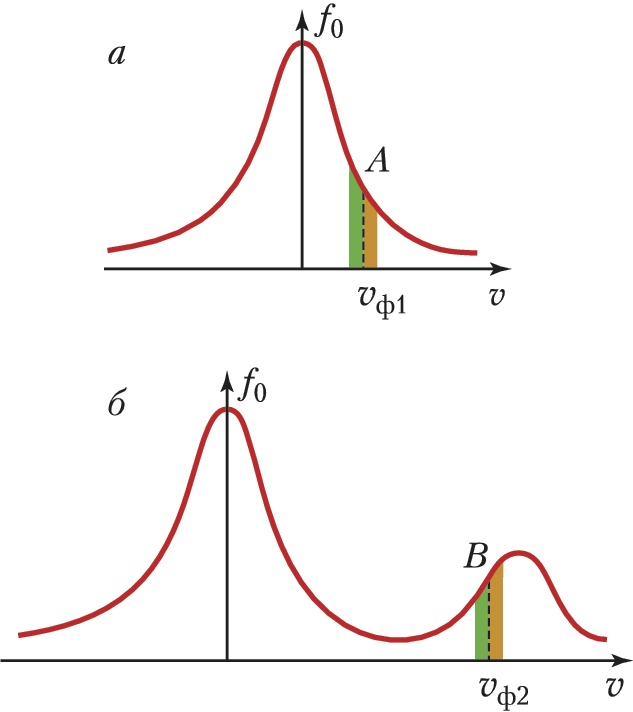
При линейном Л. з. происходит обмен энергией между бегущей плазменной волной с потенциалом$φ(\boldsymbol r,t)= =φ_0\exp(\boldsymbol{𝑘r}-ωt)$ ($φ_0$ – амплитуда, $\boldsymbol k$ – волновой вектор, $\boldsymbol r$ – радиус-вектор, $ω$ – частота, $t$ – время) и резонансными электронами (а для ионно-звуковых волн – также и ионами), скорости $v$ которых в направлении распространения волны близки к её фазовой скорости $v_{ф1}=ω/𝑘: v≈v_{ф1}$. Обгоняющие волну $(v_1≳v_{ф1})$ резонансные электроны отдают ей энергию и тормозятся (рис. 1), отстающие от волны $(v_2≲v_{ф1})$ электроны отбирают энергию и ускоряются. Если распределение электронов по скоростям $f_0(v)$ описывается Максвелла распределением, т. е. отстающих от волны частиц (зелёная область А на рис. 2,а) больше, чем обгоняющих (оранжевая область А на рис. 2,а), то в среднем волна отдаёт энергию электронам и её амплитуда $φ(t)=φ_0 \exp(γt)$ уменьшается с декрементом затухания $γ<0$. При наличии магнитного поля Л. з. возникает только для частиц, у которых близки проекции скоростей на направление магнитного поля $H$ и фазовой скорости волны $v_{ф1}$. Это происходит на частотах $ω-nω_H$, где $ω_H$ – циклотронная частота электронов ($n=0$ соответствует обычному Л. з., $n=±1,±2,...$ – т. н. циклотронному Л. з.). В поперечном к магнитному полю направлении передачи энергии не происходит: на одном обороте ларморовской окружности частица получает и отдаёт одинаковую энергию.
Если в плазме присутствует высокоскоростной электронный пучок (рис. 2,б), то преобладают обгоняющие волну резонансные электроны со скоростью $v≳v_{ф2}$ (оранжевая область В на рис. 2,б), поэтому волна будет отбирать энергию у электронов, её собств. энергия растёт – развивается пучковая неустойчивость (происходит т. н. обратное Л. з.).
Нелинейное Л. з. имеет место при возбуждении электростатич. волны конечной амплитуды $φ_0$. Резонансные частицы захватываются в потенциальную яму электрич. поля и колеблются в ней с частотой $\omega_{нл}=k\sqrt{e\varphi_0/m }$ ($e$ – заряд электрона). Если $γ>ω_{нл}$, то волна затухает раньше, чем успевают проявиться нелинейные эффекты. При $γ<ω_{нл}$ происходит циклич. обмен энергий между волной и осциллирующими частицами, вследствие чего функция распределения частиц вблизи резонансных скоростей осциллирует. Однако за время $t⩾1/ω_{нл}$ происходит уравнивание числа опережающих и отстающих частиц, вследствие чего в плазме устанавливается стационарная волна, а в окрестности резонанса формируется плато функции распределения электронов.
Эффект Л. з. существен в физике разреженной плазмы, в частности космической.