МАНДЕЛЬШТА́МА – БРИЛЛЮЭ́НА РАССЕ́ЯНИЕ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
МАНДЕЛЬШТА́МА – БРИЛЛЮЭ́НА РАССЕ́ЯНИЕ, рассеяние световых волн, сопровождающееся изменением их частоты, на адиабатич. флуктуациях плотности конденсиров. сред. Частóты падающих и рассеянных волн различаются на частоту тепловых упругих волн в среде. М. – Б. р. предсказано независимо Л. И. Мандельштамом (1918) и Л. Бриллюэном (1922) и обнаружено (1930) экспериментально Г. С. Ландсбергом и Мандельштамом в кристаллах и Е. Ф. Гроссом в жидкостях.
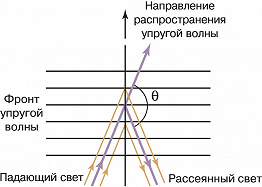
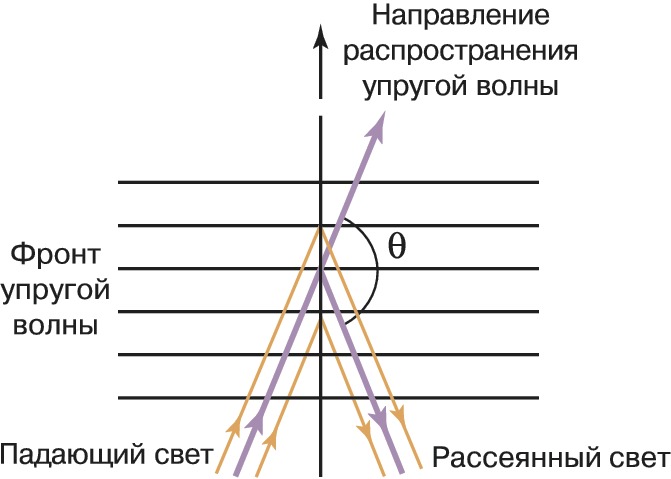
Классич. трактовка М. – Б. р. заключается в следующем. Флуктуации плотности, возникающие в среде благодаря хаотич. тепловому движению молекул, можно представить как результат наложения (интерференции) упругих волн разл. частоты со случайными амплитудами и фазами, распространяющихся во всевозможных направлениях. Каждая упругая волна модулирует диэлектрич. проницаемость среды, создавая бегущую со скоростью звука дифракционную решётку, т. к. в местах повышенной плотности показатель преломления больше, чем в области разрежения. Дифракция плоской световой волны с частотой ω и волновым вектором 𝑘 на такой решётке приводит к появлению рассеянной волны, которая распространяется под углом θ к падающей (рис. 1) и имеет частоту, отличающуюся от ω на частоту упругой волны Ω. Угол рассеяния θ и частота Ω при этом связаны соотношением Ω = 2nω(v/c)sin(θ/2), где c – скорость света в вакууме, n – показатель преломления среды, v – скорость звука. Если волновой вектор упругой волны q составляет острый угол с вектором 𝑘, то частота рассеянной волны равна ωs = ω-Ω (стоксова компонента); если этот угол тупой, то рассеянная волна имеет частоту ωa = ω+Ω (антистоксова компонента). Поскольку в среде имеются тепловые упругие волны всевозможных частот и направлений, под заданным углом θ будут наблюдаться одновременно стоксова и антистоксова компоненты – т. н. дублет Мандельштама – Бриллюэна. Спектральная ширина рассеянных компонент при фиксиров. значении θ определяется затуханием упругих волн.
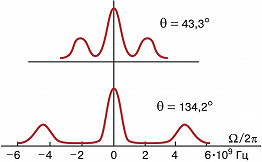
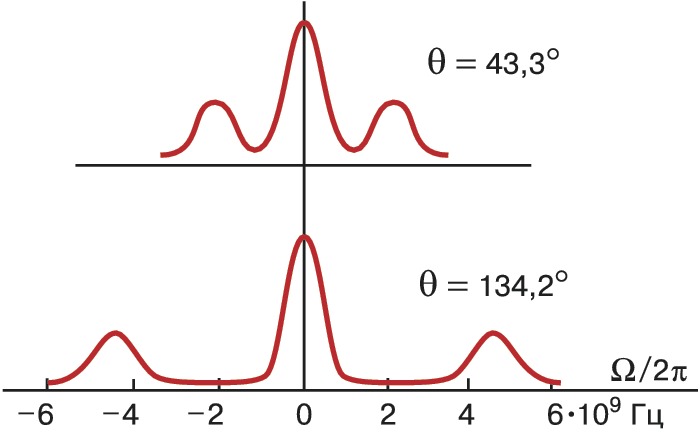
Дублетная структура спектра имеет место при рассеянии в плотных газах и в жидкостях (рис. 2). В твёрдых телах из-за наличия сдвиговых упругих волн, имеющих скорость, отличную от v, структура спектра становится более сложной. Типичные значения сдвигов частот при М. – Б. р. имеют порядок величины 109–1010 Гц, т. е. фактически речь идёт о рассеянии света на гиперзвуковых колебаниях.
В квантовой теории М. – Б. р. описывается как рассеяние фотонов с частотой ω на фононах – квазичастицах, соответствующих упругим волнам. Каждый фонон имеет энергию ℏΩ и импульс ℏq. При стоксовом рассеянии в каждом элементарном акте исчезает один фотон падающего излучения и одновременно появляются фотон со стоксовой частотой ωs = ω-Ω и фонон с частотой Ω. Соответственно, рождение фотона на антистоксовой частоте ωa = ω+Ω сопровождается исчезновением фонона с частотой Ω .
При малых интенсивностях падающего излучения световые волны не оказывают заметного влияния на состояние среды и рассеяние происходит только на тепловых упругих волнах (тепловых фононах). В этом случае говорят о спонтанном М. – Б. р. Интенсивность рассеянных компонент составляет при этом примерно 10–5–10–6 интенсивности падающей волны. При использовании мощных пучков лазерного излучения возникает вынужденное М. – Б. р. В этом случае падающая световая волна совместно с рассеянной стоксовой компонентой усиливает те упругие волны, которые вызвали первоначальное спонтанное рассеяние. Усиление упругих волн происходит за счёт действия электрострикционной силы, втягивающей молекулы в те области, где электрич. поле интерферирующих световых волн больше. Увеличение амплитуды упругой волны приводит к росту амплитуды рассеянной стоксовой компоненты, что, в свою очередь, вызывает дальнейшее усиление упругой волны, и т. д. В результате интенсивность стоксовой компоненты может стать сравнимой с интенсивностью падающей волны (накачки).
На квантовом языке усиление упругой волны означает генерацию значит. потока фононов, возникающих при стоксовом рассеянии. Т. к. при антистоксовом рассеянии имеет место поглощение фононов, то вынужденное рассеяние в антистоксову (высокочастотную) область отсутствует.
В реальных лазерных пучках при вынужденном М. – Б. р. наиболее эффективное усиление испытывает стоксова волна, распространяющаяся навстречу волне накачки. При этом генерируется мощная гиперзвуковая волна, направленная в ту же сторону, что и волна накачки.
Спонтанное М. – Б. р. широко используется для исследования свойств вещества. Спектры рассеяния позволяют определять скорость и затухание звуковых волн, находить упругие константы и коэф. вязкости, исследовать особенности межмолекулярных взаимодействий и т. п. Вынужденное М. – Б. р. используется для преобразования интенсивного лазерного излучения, генерации коротких световых импульсов и мощных гиперзвуковых волн. Широко используется также эффект обращения волнового фронта, имеющий место при вынужденном рассеянии Мандельштама – Бриллюэна.