ЛИ́НЗА
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
ЛИ́НЗА оптическая, прозрачное тело, ограниченное двумя преломляющими световые лучи поверхностями, способное формировать оптич. изображения предметов. Л. является одним из осн. элементов оптич. систем. Наиболее часто используются Л., поверхности которых имеют общую ось симметрии и сферич. форму, реже – цилиндрическую, конусообразную и др. Л. изготавливают для видимой области спектра из оптич. или органич. стекла, для УФ-диапазона – из кварца, флюорита, для ИК-диапазона – из стекла спец. сорта, германия, сапфира и др.
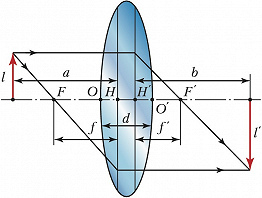
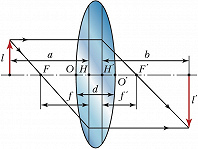
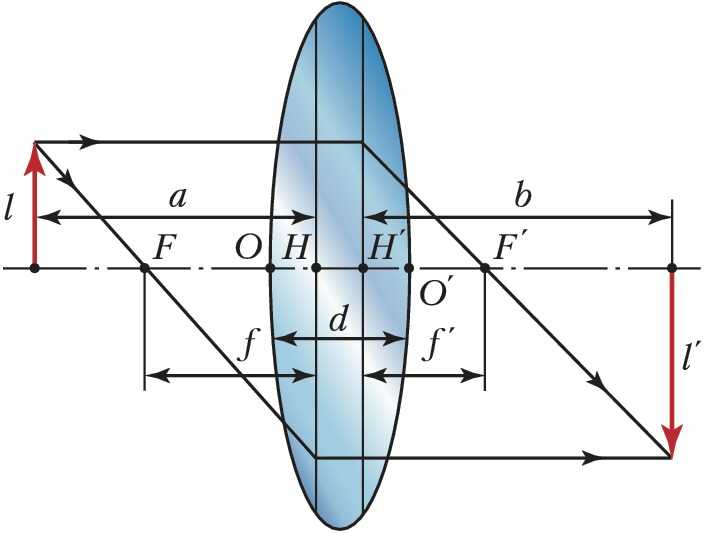
При анализе оптич. свойств Л. обычно рассматривают параксиальный световой пучок (распространяющийся под малым углом к оси). Ход параксиальных лучей обусловлен положением кардинальных точек Л. – гл. точек и гл. фокусов Л. (рис.). Гл. точки $H$ и $H′$ определяются пересечением оптич. оси с главными плоскостями, представляющими собой сопряжённые плоскости, взаимное изображение которых оптич. система даёт без увеличения. Гл. фокусы $F$ и $F′$ являются изображениями точек, лежащих на оптич. оси по обе стороны Л. и бесконечно удалённых от неё. Отрезки $HF=f$ и $H′F′=f′$ – переднее и заднее фокусные расстояния Л. Если направление фокусного расстояния совпадает с направлением лучей света, фокусное расстояние считается положительным; если направления противоположны – отрицательным (на рис. $f<0$, $f′ >0$). Если среды по обе стороны Л. имеют одинаковый показатель преломления, то $|f|= |f′|$. Точки пересечения $О$ и $О′$ поверхностей Л. с осью называются вершинами, а расстояние $d$ между ними – толщиной линзы.
Преломляющие свойства Л. зависят от радиусов кривизны сферич. поверхностей $r_1$ и $r_2$, толщины линзы $d$ и показателя преломления $n$ вещества. Л. называется тонкой, если $d≪r_1$ и $d≪r_2$. Мерой преломляющего действия Л. служит её оптич. сила $\Phi=1/f'$, измеряемая в диоптриях (м–1):$$ \Phi =(n-1) \left (\frac{1}{r_1}-\frac{1}{r_2}\right )+\frac{(n-1)^2d}{nr_1r_2}.$$
Л., преобразующая параллельный световой пучок в сходящийся, называется собирающей (положительной, $\Phi>0$); после прохождения такой Л. параллельные лучи пересекаются в гл. фокусе $F′$. Л., преобразующая параллельный пучок в расходящийся, называется рассеивающей (отрицательной, $\Phi<0$); после её прохождения параллельные лучи не пересекаются, но в гл. фокусе $F$, лежащем в области распространения параллельного пучка, пересекаются их продолжения. Существуют Л. (называемые афокальными), после прохождения которых параллельный пучок остаётся параллельным. Положительные Л. дают действительные изображения предметов, находящихся до переднего фокуса Л. (левее $F$), и всех мнимых объектов, находящихся за Л. Рассеивающие Л. дают прямое уменьшенное мнимое изображение объектов, расположенных между Л. и её передним фокусом. Взаимное положение предмета и изображения, а также увеличение линзы $\text{Γ}$ определяются формулами$$\frac{f}{a}+\frac{f'}{b}=1, \; \text{Γ}= \frac{l'}{l}=-\frac{f}{a-f}.$$
Здесь $a$ и $b$ – расстояния от гл. точек до предмета и изображения соответственно, $l$ и $l′$ – размеры предмета и изображения.
Тонкие Л., играющие роль фазовых корректоров, используются для преобразования когерентных световых пучков. При прохождении когерентного пучка через тонкую Л. к распределению его фазы добавляется составляющая, являющаяся функцией удаления от оси. Распределение комплексной амплитуды поля в фокальной плоскости Л. с точностью до фазового множителя является фурье-образом распределения амплитуды поля перед Л. Такие Л. широко используются в системах пространственной фильтрации излучения.
Л. обладают всеми аберрациями, присущими центрированным оптич. системам (см. Аберрации оптических систем). Особенно важно учитывать аберрации при использовании широкополосных световых пучков. Для исправления сферич. аберрации и комы комбинируют Л. разл. формы и Л. из материалов с разл. дисперсией.