КАРДИНА́ЛЬНЫЕ ТО́ЧКИ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
КАРДИНА́ЛЬНЫЕ ТО́ЧКИ оптич. системы, точки на оси $OO'$ центрированной оптич. системы, позволяющие строить изображение произвольной точки пространства объектов в параксиальной области (вблизи оптич. оси).
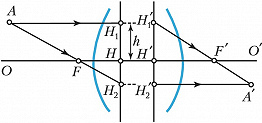
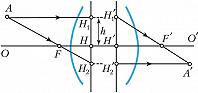
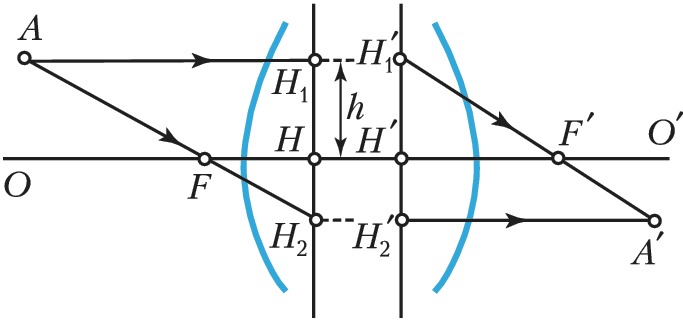
Обычно К. т. оптич. системы служат 4 точки: передний $F$ и задний $F'$ фокусы, передняя $H$ и задняя $H'$ главные точки (рис.). Задний фокус является изображением бесконечно удалённой точки, расположенной на оптич. оси в пространстве объектов, а передний фокус – изображением в пространстве объектов бесконечно удалённой точки пространства изображений. Главные точки – это точки пересечения с оптич. осью главных плоскостей – сопряжённых плоскостей, взаимное изображение которых оптич. система даёт без увеличения, т. е. всякая точка $H_1$, расположенная в главной плоскости на расстоянии $h$ от оси, изображается в др. главной плоскости в точке $H'_1$ на том же расстоянии $h$ от оси, что и точка $H_1$. (На рис. изображены сечения главных плоскостей, проходящих соответственно через точки $H_1$, $H_2$ и $H'_1$, $H'_2$ и расположенных перпендикулярно плоскости рисунка.) Расстояние от точки $H$ до точки $F$ называтся передним фокусным расстоянием (отрицательным на рис., т. к. направление от $H$ к $F$ противоположно ходу световых лучей), а расстояние от точки $H'$ до точки $F'$ – задним фокусным расстоянием (положительным на рис., т. к. направление от $H'$ к $F'$ совпадает с ходом лучей). Построение изображения $A'$ произвольной точки $A$ с помощью этих четырёх точек показано на рисунке. Луч из точки $A$, проходящий через передний фокус $F$ и переднюю главную плоскость $H_1H_2$, направляется системой параллельно оптич. оси $OO'$, а луч, идущий из точки $A$ параллельно $OO'$ и пересекающий заднюю главную плоскость $H'_1H'_2$ после преломления в системе, проходит через задний фокус $F'$. Точка пересечения $A'$ этих двух лучей является изображением точки $A$, формируемым оптич. системой. Любой параксиальный луч, исходящий из точки $A$, по выходе из системы проходит через точку $A'$.
В бесконечно тонкой линзе обе главные плоскости сливаются в одну. У телескопич. системы К. т. находятся на бесконечности, поэтому построение изображения с их помощью невозможно. В этом случае можно разбить телескопич. систему на 2 части (напр., на объектив и окуляр) и построить изображение любой точки пространства объектов в отдельности для каждой части.