КРИСТАЛЛОО́ПТИКА

КРИСТАЛЛОО́ПТИКА (оп­ти­ка ани­зо­троп­ных сред), изу­ча­ет за­ко­ны и осо­бен­но­сти рас­про­стра­не­ния све­та в кри­стал­лах, оп­ре­де­ляе­мые их атом­ным строе­ни­ем. Т. к. пе­ри­од кри­стал­ли­че­ской ре­шёт­ки

(по­ряд­ка 1 нм) во мно­го раз мень­ше дли­ны вол­ны ви­ди­мо­го све­та ($λ=400–700$ нм), кри­сталл мож­но рас­смат­ри­вать как од­но­род­ную, но ани­зо­троп­ную сре­ду. На­ча­ло К. по­ло­жи­ло от­кры­тие дат. учё­ным Э. Бар­то­ли­ном в 1669 двой­но­го лу­че­пре­лом­ле­ния в кри­стал­лах каль­ци­та.

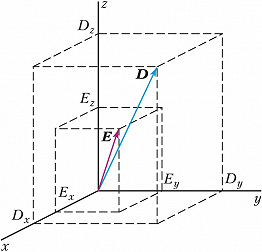
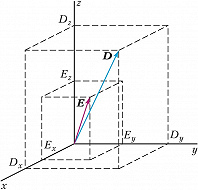
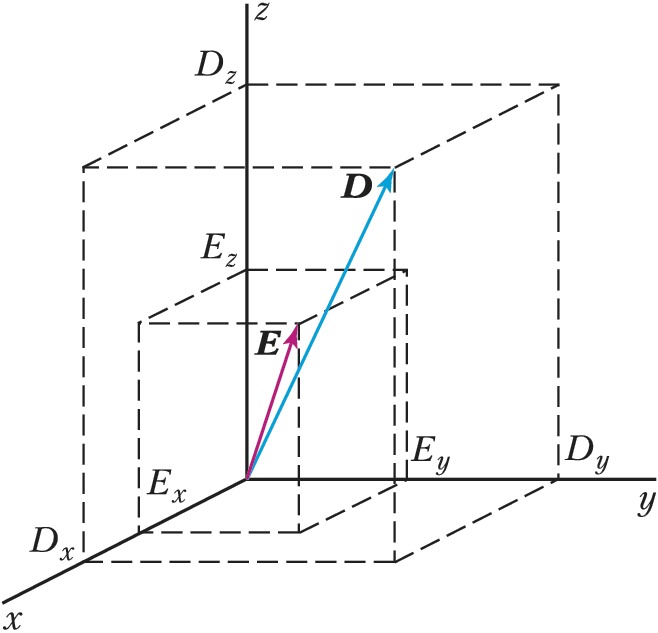
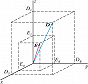
В ани­зо­троп­ных про­зрач­ных не­маг­нит­ных сре­дах связь ме­ж­ду на­пря­жён­но­стя­ми $\boldsymbol E$, $\boldsymbol H$ и ин­дук­ция­ми $\boldsymbol D$, $\boldsymbol B$ элек­трич. и маг­нит­но­го по­лей све­то­вой вол­ны за­пи­сы­вае­тся в ви­де:  $$D_i=\varepsilon_{ik}^0E_k,\quad B_i=\mu_iH_i,\tag 1$$ где $\varepsilon_{ik}^0$ – тен­зор ди­элек­трич. про­ни­цае­мо­сти с гл. зна­че­ния­ми $ε_x, ε_y, ε_z$ (со­ответ­ст­вую­щие по­ка­за­те­ли пре­лом­ле­ния $n_i=\sqrt {\varepsilon_i}$), за­ви­ся­щий от на­прав­ле­ния вол­но­вой нор­ма­ли $\boldsymbol N$, час­то­ты $ω$ (час­тот­ная дис­пер­сия) и вол­но­во­го век­то­ра $𝑘$ (про­стран­ст­вен­ная дис­пер­сия); тен­зор маг­нит­ной про­ни­цае­мо­сти $μ_i=1$. В об­щем слу­чае зна­че­ния $ε_x, ε_y, ε_z$ не рав­ны ме­ж­ду со­бой, по­это­му для всех на­прав­ле­ний, кро­ме глав­ных, $\boldsymbol D$ и $\boldsymbol E$ не сов­па­да­ют по на­прав­ле­нию (рис. 1).

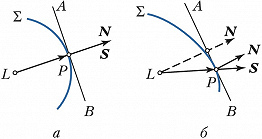
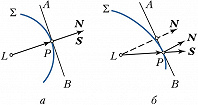
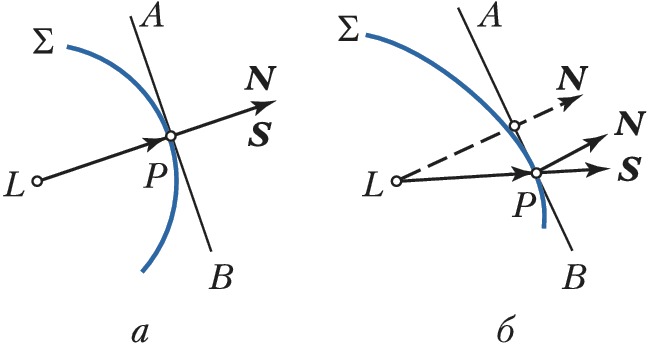
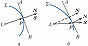
В от­ли­чие от изо­троп­ных сред (рис. 2, а), в кри­стал­лах по за­дан­но­му на­прав­ле­нию $\boldsymbol N$ мо­гут рас­про­стра­нять­ся две пло­ские ли­ней­но по­ля­ри­зо­ван­ные в раз­ных плос­ко­стях с раз­ны­ми по­каза­те­ля­ми пре­лом­ле­ния $n_{1,2}$ све­то­вые вол­ны с вол­но­вы­ми век­то­ра­ми $\boldsymbol k_{1,2}= (ω /c)n_{1,2}\boldsymbol N$ и разл. фа­зо­вы­ми ско­ро­стя­ми $v_{1,2}=c/n_{1,2}$, ко­то­рые за­ви­сят от на­прав­ле­ния. Для ани­зо­троп­ной cре­ды (рис. 2,б) вол­но­вая по­верх­ность в мо­мент вре­ме­ни $t$, соз­да­вае­мая вол­ной, ис­хо­дя­щей из точ­ки $L$, от­лич­на от сфе­ри­че­ской, ха­рак­тер­ной для изо­троп­ной сре­ды. На­прав­ле­ние рас­про­стра­не­ния по­верх­но­сти по­сто­ян­ной фа­зы (нор­маль $N$ к вол­но­вой по­верх­но­сти $Σ$, рис. 2,б) не сов­па­да­ет с лу­чом $\boldsymbol S$, ука­зы­ваю­щим на­прав­ле­ние рас­про­стра­не­ния энер­гии (ра­ди­ус-век­тор $LP$). Ско­ро­сти пе­ре­но­са энер­гии (лу­че­вые ско­ро­сти) свя­за­ны со­от­но­ше­ни­ем $v'_{1,2}=v_{1,2}/ \cos \alpha$, где $α$ – угол ме­ж­ду век­то­ра­ми $\boldsymbol E$ и $\boldsymbol D$.

По­ка­за­те­ли пре­лом­ле­ния кри­стал­ла $n_{1,2}$ и ско­ро­сти волн $v_{1,2}$ в на­прав­ле­нии $\boldsymbol N$ оп­ре­де­ля­ют­ся из осн. урав­не­ния К. – урав­не­ния нор­ма­лей (урав­не­ния Фре­не­ля):  $$N_x^2/(n^{–2}-\varepsilon_x^{-1})+N_y^2/(n^{–2}-\varepsilon_y^{-1})+N_z^2/(n^{–2}-\varepsilon_z^{-1})=1.\tag2$$

Свой­ст­ва кри­стал­ла мож­но опи­сать гео­мет­ри­че­ски разл. по­верх­но­стя­ми. Обыч­но ис­поль­зу­ют­ся оп­тич. ин­ди­кат­ри­са (по­верх­ность вол­но­вых нор­ма­лей), пред­став­ляю­щая со­бой эл­лип­со­ид с по­лу­ося­ми, про­пор­цио­наль­ны­ми главным по­ка­за­те­лям пре­лом­ле­ния $n_x, n_y, n_z$, и эл­лип­со­ид Фре­не­ля (по­верх­ность лу­че­вых нор­ма­лей) – эл­лип­со­ид с по­лу­ося­ми, рав­ны­ми лу­че­вым ско­ро­стям све­та в кри­стал­ле.

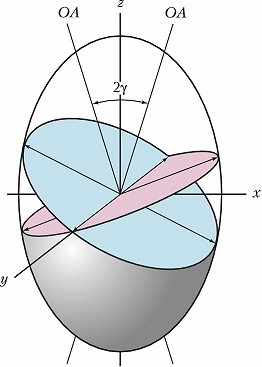
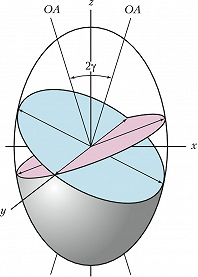
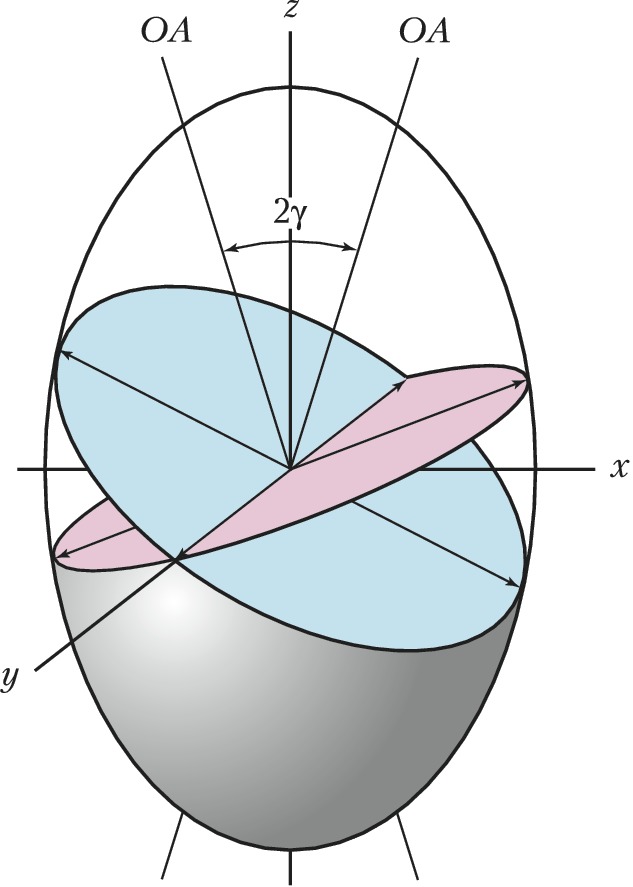
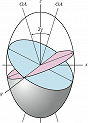
В об­щем слу­чае лю­бой эл­лип­со­ид (в ча­ст­но­сти, оп­тич. ин­ди­кат­ри­са) име­ет два кру­го­вых се­че­ния, про­хо­дя­щих че­рез его центр и рас­по­ло­жен­ных сим­мет­рич­но от­но­си­тель­но его главных осей (рис. 3). По­это­му кри­сталл в об­щем слу­чае име­ет две оп­тич. оси, угол ме­ж­ду ко­то­ры­ми $2γ$ за­ви­сит от фор­мы эл­лип­сои­да, т. е. от сим­мет­рии (син­го­нии) кри­стал­ла. От­счёт уг­ла $γ$ про­из­во­дит­ся от боль­шой оси $z$ ин­ди­кат­ри­сы и вы­чис­ля­ет­ся по фор­муле $\mathrm{tg} \gamma=\sqrt {ε_z(ε_y-ε_x)/ε_x(ε_z-ε_y)}$ (принято счи­тать $ε_x<ε_y<ε_z$). Ес­ли $(ε_y-ε_x)< <(ε_z-ε_y)$, то угол $γ<45°$, ост­рой биc­сектрисой яв­ля­ет­ся ось $z$ и кри­сталл поло­жи­тель­ный; ес­ли $(ε_y-ε_x)> (ε_z-ε_y)$, то угол $γ>45°$ и ост­рой биcсектрисой яв­ля­ет­ся ось $x$, кри­сталл от­ри­ца­тель­ный. Из-за дис­пер­сии воз­мож­ны слу­чаи, ко­гда один и тот же кри­сталл оп­ти­че­ски по­ло­жи­те­лен для од­ной дли­ны вол­ны све­та и от­ри­ца­те­лен для дру­гой.

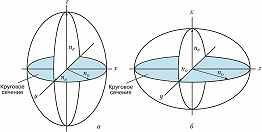
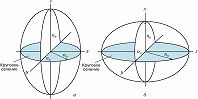
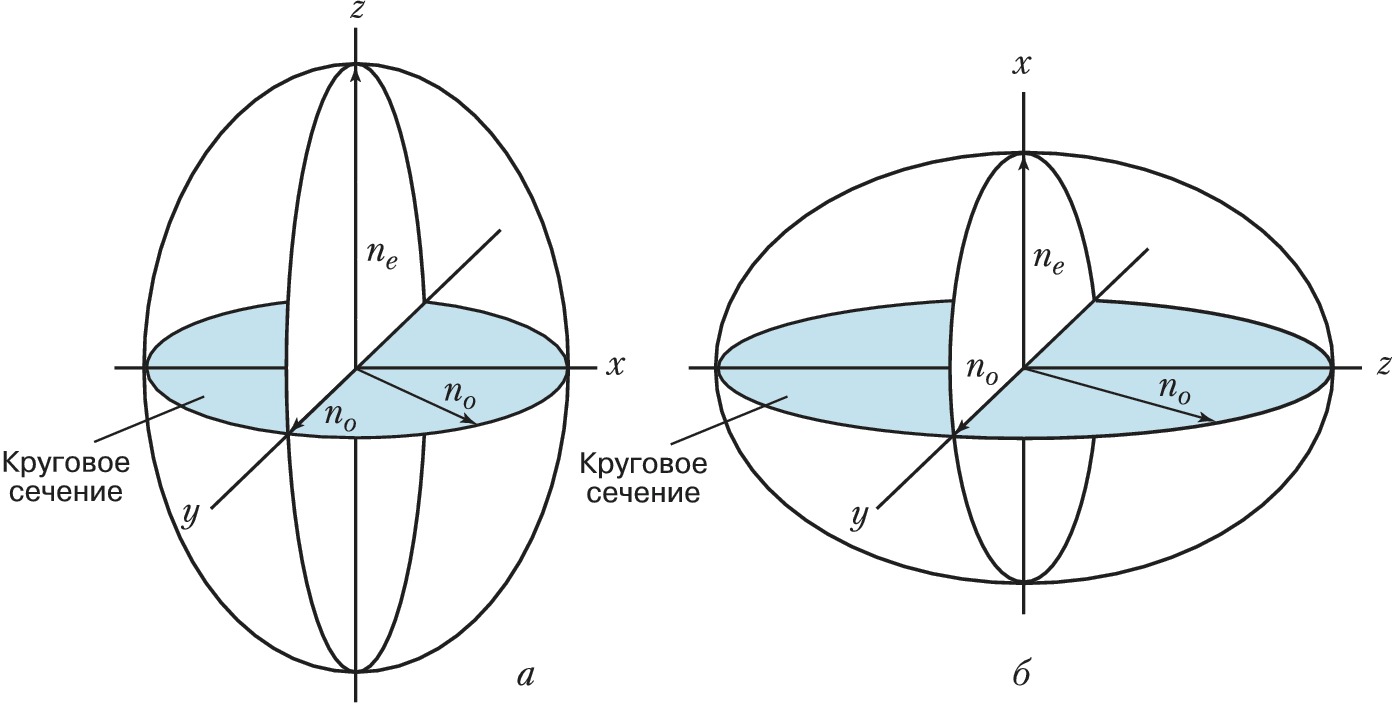
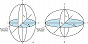
Ес­ли оба кру­го­вых се­че­ния сов­па­да­ют друг с дру­гом, то сов­па­да­ют и обе оси – кри­сталл од­но­ос­ный. В этом слу­чае эл­лип­со­ид яв­ля­ет­ся эл­лип­сои­дом вра­ще­ния, его ось сов­па­да­ет с од­ним из гл. на­прав­ле­ний кри­стал­ла. В та­ких кри­с­тал­лах в лю­бом на­прав­ле­нии (кро­ме оси) мо­гут рас­про­стра­нять­ся две вол­ны: од­на со ско­ро­стью $v_о$ и по­ка­за­те­лем пре­лом­ле­ния $n_о$, не за­ви­ся­щи­ми от на­прав­ле­ния, – обык­но­вен­ная вол­на и дру­гая – с за­ви­ся­щи­ми от на­прав­ле­ния по­ка­за­телем пре­лом­ле­ния $n_e$ и ско­ро­стью $v_e$ – не­обык­но­вен­ная вол­на. Ес­ли $n_x=n_y=n_о\lt n_z=n_е (v_o \gt v_e)$, кри­стал­лы на­зы­ва­ют­ся по­ло­жи­тель­ны­ми (рис. 4,а); ес­ли $n_y=n_z=n_о\gt n_x=n_е (v_o\lt v_e)$ – от­рица­тель­ны­ми (рис. 4,б). Вдоль оп­тич. оси $n_e=n_o$ и $v_e=v_o$, в этом слу­чае двой­ное лу­че­пре­лом­ле­ние от­сут­ст­ву­ет. Ес­ли $n_x=n_y=n_z$, то эл­лип­со­ид об­ра­ща­ет­ся в сфе­ру, все его се­че­ния кру­го­вые – сре­да оп­ти­че­ски изо­троп­на.

В дву­ос­ных кри­стал­лах кру­го­вым се­че­ни­ям оп­тич. ин­ди­кат­ри­сы со­от­вет­ст­ву­ют оп­тич. оси (би­нор­ма­ли), а в эл­лип­сои­де Фре­не­ля – лу­че­вые оп­тич. оси (би­ра­диа­ли). В од­но­ос­ных кри­стал­лах би­нор­ма­ли и би­ра­диа­ли сов­па­да­ют. Прак­ти­че­ски нор­маль­ные и лу­че­вые ско­ро­сти столь близ­ки, что их раз­ли­чие про­яв­ля­ет­ся толь­ко в яв­ле­нии ко­ни­че­ской реф­рак­ции

.

Осн. оп­тич. кон­стан­ты кри­стал­лов – по­ка­за­те­ли пре­лом­ле­ния, ко­то­рые час­то слу­жат их ди­аг­но­стич. при­зна­ком. Изо­троп­ным кри­стал­лом яв­ля­ет­ся ал­маз с по­ка­за­те­лем пре­лом­ле­ния $n= 2,419$ при $λ=589$ нм; ани­зо­троп­ный ис­ланд­ский шпат име­ет $n_о= 1,658, n_е= 1,486$ при той же дли­не вол­ны. Ок. 50% кри­стал­лов име­ют ср. по­ка­за­тель пре­лом­ле­ния в пре­де­лах от 1,5 до 1,7. Ин­те­рес­но рас­пре­де­ле­ние кри­стал­лов по ос­но­сти и оп­тич. зна­ку: изо­троп­ные – 14,9%, од­но­ос­ные по­ло­жи­тель­ные – 6,8%, од­но­ос­ные от­ри­ца­тель­ные – 13,8%, не­оп­ре­де­лён­ные – 2,4%, дву­ос­ные по­ло­жи­тель­ные – 30,3%, дву­ос­ные от­ри­ца­тель­ные – 31,8%.

Две све­то­вые вол­ны с ор­то­го­наль­ной по­ля­ри­за­ци­ей, рас­про­стра­няю­щие­ся в кри­стал­ле в од­ном на­прав­ле­нии, за счёт раз­ли­чия по­ка­за­те­лей пре­лом­ле­ния при­об­ре­та­ют раз­ность фаз. С по­мо­щью по­ля­ри­за­ци­он­но­го уст­рой­ст­ва мож­но све­сти на­прав­ле­ния ко­ле­ба­ний в вы­шед­ших вол­нах в од­ну плос­кость и на­блю­дать их ин­тер­фе­рен­цию (см. Ин­тер­фе­рен­ция по­ля­ри­зо­ван­ных лу­чей

). Ин­тер­фе­рен­ция в кри­стал­лич. пла­стин­ках ис­поль­зу­ет­ся для соз­да­ния ком­пен­са­то­ров оп­ти­че­ских

 >>

, ин­тер­фе­рен­ци­он­но-по­ля­ри­за­ци­он­ных фильт­ров и т. п. Фи­гу­ры ин­тер­фе­рен­ции, ко­то­рые по­лу­ча­ют­ся в схо­дя­щем­ся све­те, на­зы­ва­ют­ся ко­но­ско­пич. фи­гу­ра­ми (см. Ко­но­ско­пия

 >>

). Их вид за­ви­сит от сим­мет­рии и ори­ен­та­ции кри­с­тал­лич. пла­стин­ки.

Ре­аль­ные кри­стал­лы все­гда в ка­кой-то об­лас­ти спек­тра по­гло­ща­ют про­хо­дя­щий свет, при­чём ме­ха­низм по­гло­ще­ния за­ви­сит от свойств сре­ды и час­то­ты из­лу­че­ния. По­гло­ще­ние све­та кри­стал­ла­ми мож­но опи­сать ком­плекс­ным тен­зо­ром ди­элек­трич. про­ни­цае­мо­сти, дей­ст­ви­тель­ные и мни­мые час­ти ко­то­ро­го свя­за­ны Кро­ни­га – Кра­мер­са со­от­но­ше­ния­ми

. Ко­эф. по­гло­ще­ния в кри­стал­лах, в от­ли­чие от изо­троп­ных сред, за­ви­сит от со­стоя­ния по­ля­ри­за­ции волн – т. н. ди­хро­изм

 >>

 и пле­ох­ро­изм

 >>

. Напр., тур­ма­лин очень силь­но по­гло­ща­ет обык­но­вен­ный луч, по­это­му при па­де­нии ес­те­ст­вен­но­го све­та из не­го вы­хо­дит не­обык­но­вен­ный луч, т. е. кри­сталл ве­дёт се­бя как по­ля­ри­за­тор.

Не­ко­то­рые кри­стал­лы, спо­соб­ные вра­щать плос­кость по­ля­ри­за­ции при про­хо­ж­де­нии че­рез них ли­ней­но по­ля­ри­зован­но­го све­та, от­но­сят­ся к оп­ти­че­ски ак­тив­ным ве­ще­ст­вам

(ги­ро­троп­ным). Оп­ти­че­ски ак­тив­ные кри­стал­лы мо­гут иметь две мо­ди­фи­ка­ции – пра­вую и ле­вую (см. Энан­тио­мор­физм

 >>

). Вра­ще­ние плос­ко­сти по­ля­ри­за­ции мо­жет про­яв­лять­ся толь­ко в изо­троп­ных сре­дах и в кри­стал­лах в на­прав­ле­нии оп­тич. осей.

Ме­то­ды К. при­ме­ня­ют­ся в разл. об­лас­тях нау­ки и тех­ни­ки для по­лу­че­ния и ана­ли­за по­ля­ри­зо­ван­но­го све­та, для со­зда­ния оп­тич. за­тво­ров, мо­ду­ля­то­ров и др., а так­же для опи­са­ния оп­тич. свойств кри­стал­лов, из­ме­няю­щих­ся при разл. внеш­них воз­дей­ст­ви­ях.