КРИСТАЛЛОАКУ́СТИКА

КРИСТАЛЛОАКУ́СТИКА, раз­дел аку­сти­ки, в ко­то­ром изу­ча­ют­ся свой­ст­ва уп­ру­гих волн в кри­стал­лах. Вслед­ст­вие ани­зо­тро­пии, в кри­стал­лах воз­ни­ка­ют прин­ци­пи­аль­но но­вые аку­стич. яв­ле­ния, не­воз­мож­ные в изо­троп­ных сре­дах. К. сфор­ми­ро­ва­лась в отд. на­прав­ле­ние ис­сле­до­ва­ний в сер. 20 в. Раз­ви­тие это­го на­прав­ле­ния сти­му­ли­ро­ва­лось не толь­ко по­треб­но­стя­ми тех­ни­ки, но и ну­ж­да­ми раз­ви­вав­ших­ся ме­то­дов фи­зи­че­ской аку­сти­ки по изу­че­нию де­фек­тов в кри­стал­лах, а так­же др. раз­де­лов аку­сти­ки, та­ких как аку­сто­элек­тро­ни­ка, аку­сто­оп­ти­ка и сейс­моа­ку­сти­ка. В ре­зуль­та­те бы­ли соз­да­ны но­вые экс­пе­рим. и тео­ре­тич. ме­то­ды, по­зво­ляю­щие ре­шать вол­но­вые за­да­чи уп­ру­го­сти в сре­дах про­из­воль­ной ани­зо­тро­пии.

В уп­ру­гом кри­стал­ле вдоль ка­ж­до­го на­прав­ле­ния, задаваемого вектором $\boldsymbol m (|\boldsymbol m|=1)$, мо­гут рас­про­стра­нять­ся три вол­ны сме­ще­ний, раз­личаю­щие­ся фа­зо­вы­ми ско­ро­стя­ми $v_α (v_1⩽v_2⩽v_3)$ и вза­им­но ор­то­го­наль­ны­ми век­то­ра­ми по­ля­ри­за­ции $\boldsymbol A_α (α=1, 2, 3)$. Та­кие вол­ны на­зы­ва­ют изо­нор­маль­ны­ми, т. к. они име­ют од­но и то же на­прав­ле­ние вол­но­вой нор­ма­ли $\boldsymbol m$. Век­то­ры по­ля­ри­за­ции не яв­ля­ют­ся чис­то про­доль­ны­ми и по­пе­реч­ны­ми, как в изо­троп­ных сре­дах. Толь­ко вдоль вы­де­лен­ных на­прав­ле­ний, на­зы­вае­мых про­доль­ны­ми нор­ма­ля­ми, один из век­то­ров по­ля­ри­за­ции ста­но­вит­ся чис­то про­доль­ным $(\boldsymbol Aα||\boldsymbol m)$, а два др. век­то­ра – чис­то по­пе­реч­ны­ми. Та­кие на­прав­ле­ния обыч­но свя­за­ны с эле­мен­та­ми сим­мет­рии кри­стал­ла, но да­же в про­из­воль­ном три­клин­ном кри­стал­ле, не имею­щем эле­мен­тов сим­мет­рии, все­гда име­ет­ся не ме­нее трёх не­за­ви­си­мых про­доль­ных нор­ма­лей [И. И. Ко­лод­нер (США), 1966].

В кри­стал­лах су­ще­ст­ву­ют и по­пе­реч­ные нор­ма­ли, вдоль ко­то­рых од­на из трёх изо­нор­маль­ных волн ока­зы­ва­ет­ся чис­то по­пе­реч­ной. Напр., для лю­бо­го на­прав­ле­ния $\boldsymbol m$ в плос­ко­сти сим­мет­рии од­на из изо­нор­маль­ных волн долж­на быть по­ля­ри­зо­ва­на ор­то­го­наль­но к этой плос­ко­сти (т. н. SH-вол­ны). По­пе­реч­ные нор­ма­ли не яв­ля­ют­ся изо­ли­ро­ван­ны­ми: да­же в трик­лин­ных кри­стал­лах они об­ра­зу­ют не­пре­рыв­ные ли­нии на еди­нич­ной сфе­ре на­прав­ле­ний $\boldsymbol m^2=1$ (Ф. И. Фё­до­ров, 1965). Про­доль­ные нор­ма­ли на той же сфе­ре за­да­ют­ся точ­ка­ми пе­ре­се­че­ния ука­зан­ных ли­ний.

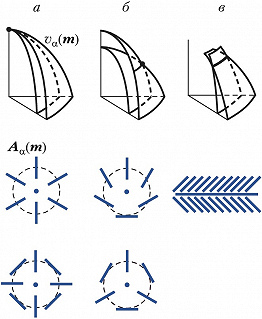
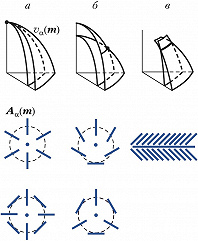
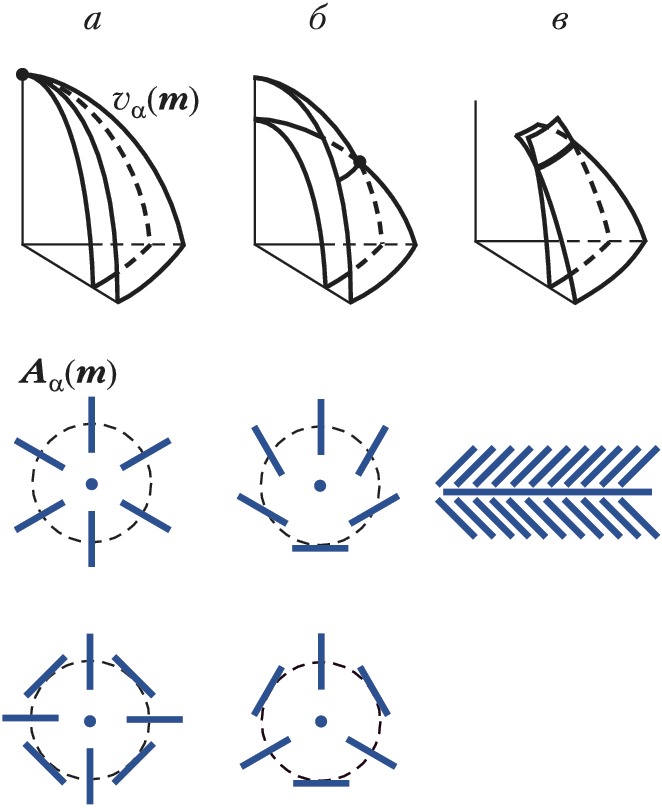
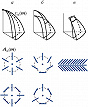
За­ви­си­мо­сти $v_α(\boldsymbol m)$ оп­ре­де­ля­ют три по­лос­ти по­верх­но­сти фа­зо­вых ско­ро­стей, ко­то­рые мо­гут со­при­ка­сать­ся друг с дру­гом лишь в вы­де­лен­ных точ­ках вы­ро­ж­де­ния, от­ве­чаю­щих на­прав­ле­ни­ям т. н. аку­сти­че­ских осей. Это ра­ди­каль­но от­ли­ча­ет кри­сталл от изо­троп­ной сре­ды, где две внутр. по­лос­ти $v_{1,2}(\boldsymbol m)$ вы­ро­ж­да­ют­ся в од­ну об­щую сфе­ру $(v_1=v_2= \mathrm {const})$, от­ве­чаю­щую по­пе­реч­ным вол­нам. В от­ли­чие от про­доль­ных и по­пе­реч­ных нор­ма­лей, аку­стич. оси не яв­ля­ют­ся обя­затель­ной при­над­леж­но­стью кри­стал­ла (хо­тя по­ка кри­стал­лы без аку­стич. осей не об­на­ру­же­ны). Аку­стич. оси в кри­стал­лах раз­ли­ча­ют­ся по гео­мет­рии кон­так­та по­лос­тей $v_α(\boldsymbol m)$, а так­же по ти­пам по­веде­ния век­тор­ных по­лей по­ля­ри­за­ции $\boldsymbol A_α(\boldsymbol m)$ в вы­ро­ж­ден­ных вет­вях вбли­зи то­чек или ли­ний вы­ро­ж­де­ния (рис.). Су­ще­ст­ву­ет пол­ная клас­си­фи­ка­ция ти­пов аку­стич. осей с ал­геб­ра­ич. при­зна­ка­ми ка­ж­до­го из них (В. И. Аль­шиц, А. В. Са­ры­чев, А. Л. Шу­ва­лов, 1985).

На­ря­ду с по­верх­но­стью фа­зо­вых ско­ро­стей удоб­ной ха­рак­те­ри­сти­кой ди­на­мич. свойств кри­стал­ла яв­ля­ет­ся т. н. по­верх­ность мед­лен­но­сти $v_\alpha^{-1} (\boldsymbol m)$. Нор­ма­ли к по­лос­тям этой по­верх­но­сти за­дают на­прав­ле­ния груп­по­вых ско­ро­стей со­от­вет­ст­вую­щих волн $v_\alpha^{гр}=𝜕v_α/𝜕\boldsymbol m$, оп­ре­де­ляю­щих ве­ли­чи­ну и на­прав­ле­ние ско­ро­сти рас­про­стра­не­ния энер­гии в вол­не. В от­ли­чие от изо­троп­ной сре­ды, где $v_\alpha^{гр}||\boldsymbol m$ для лю­бо­го на­прав­ле­ния $\boldsymbol m$, в кри­стал­лах это свой­ст­во реа­ли­зу­ет­ся лишь для вы­де­лен­ных на­прав­ле­ний, напр. для про­доль­ных нор­ма­лей.

Основные типы акустических осей (вырождений), различающиеся по геометрии контакта полостей поверхности фазовых скоростей и по особенностям полей поляризаций вблизи акустических осей. Показаны фрагмент...

Бла­го­да­ря су­ще­ст­во­ва­нию т. н. ко­ни­че­ских то­чек и ли­ний кли­но­во­го вы­ро­ж­де­ния (рис., б и в), воз­ни­ка­ют яв­ле­ния внут­рен­ней ко­ни­че­ской [Дж. Клерк, М. Масгрейв (Ве­ли­ко­бри­та­ния), 1955] и кли­но­вой [Э. Хен­не­ке, Р. Грин (США), 1969] реф­рак­ции, ко­гда ци­лин­д­рич. пу­чок при пе­ре­хо­де из изо­троп­ной сре­ды в кри­сталл рас­про­стра­ня­ет­ся да­лее по ко­ну­су или кли­ну. 

По­сколь­ку на­прав­ле­ние по­то­ка энер­гии аку­стич. вол­ны $\boldsymbol P||\boldsymbol v_\alpha^{гр}$ не кол­ли­не­ар­но вол­но­вой нор­ма­ли $\boldsymbol m$, то вол­но­вой па­кет, рас­про­стра­няю­щий­ся в те­лес­ном уг­ле вол­но­вых нор­ма­лей $δΩ_\boldsymbol m$, пе­ре­но­сит энер­гию в дру­гом те­лес­ном уг­ле $δΩ_\boldsymbol P$. В кри­стал­лах су­ще­ст­ву­ют осо­бые на­прав­ле­ния кон­цен­три­ро­ва­ния энер­гии, вбли­зи ко­то­рых $δΩ_\boldsymbol P≪δΩ_\boldsymbol m$. Та­кие на­прав­ле­ния от­ве­ча­ют на по­верх­но­сти мед­лен­но­сти точ­кам ну­ле­вой кри­виз­ны. В ок­ре­ст­но­сти этих то­чек воз­ни­ка­ет яв­ле­ние фо­нон­ной фо­ку­си­ров­ки, не­воз­мож­ное в изо­троп­ных сре­дах [Дж. Воль­фе (США), 1991].

По­верх­но­ст­ные аку­сти­че­ские вол­ны в кри­стал­лах по сво­им свой­ст­вам го­раздо раз­но­об­раз­нее, чем в изо­троп­ных сре­дах. Глу­би­на ло­ка­ли­за­ции волн в слу­чае ани­зо­троп­ной сре­ды не обя­за­тель­но по­ряд­ка дли­ны вол­ны: в ок­ре­ст­но­сти не­ко­то­рых осо­бых на­прав­ле­ний в кри­стал­ле по­верх­но­ст­ная вол­на мо­жет быть ква­зи­объ­ём­ной (В. Н. Лю­би­мов, Д. Г. Сан­ни­ков, 1973) и да­же объ­ём­ной [В. И. Аль­шиц, Е. Ло­те (Нор­ве­гия), 1979]. По ана­ло­гии с изо­троп­ной сре­дой, спра­вед­ли­ва тео­ре­ма о том, что в ка­ж­дом на­прав­ле­нии на лю­бом сре­зе про­из­воль­но­го кри­стал­ла су­ще­ст­ву­ет един­ст­вен­ная по­верх­но­ст­ная вол­на, ко­то­рая мед­лен­ней объ­ём­ных волн для то­го же на­прав­ле­ния [Д. Бар­нетт (США), Е. Ло­те, 1985]. В от­ли­чие от изо­троп­ных сред, в кри­стал­лах воз­мож­но су­ще­ст­во­ва­ние и сверх­зву­ко­вых по­верх­но­ст­ных волн. Од­на­ко они су­ще­ст­ву­ют толь­ко для вы­де­лен­ных ори­ен­та­ций (А. Н. Да­рин­ский и др., 1996) и при воз­му­ще­нии гео­мет­рии пре­вра­ща­ют­ся в т. н. от­те­каю­щие по­верх­но­ст­ные вол­ны, со­дер­жа­щие ма­лую объ­ём­ную ком­по­нен­ту, от­во­дя­щую энер­гию в глубь кри­стал­ла. От­те­каю­щие вол­ны не су­ще­ст­ву­ют в изо­троп­ных сре­дах, а в кри­стал­лах на­блю­да­ют­ся экс­пе­ри­мен­таль­но и при­ме­ня­ют­ся в тех­ни­ке.

В пье­зо­элек­трич. кри­стал­лах, на­ря­ду с опи­сан­ны­ми по­верх­но­ст­ны­ми вол­на­ми рэ­ле­ев­ско­го ти­па, воз­ни­ка­ют до­пол­нит. ло­ка­ли­зо­ван­ные мо­ды ти­па волн Гу­ляе­ва – Блю­штей­на [Ю. В. Гу­ля­ев, 1969; Л. Блю­штейн (США), 1968], ко­то­рые на­шли мно­го­числ. при­ме­не­ния в совр. тех­ни­ке. Ко­гда плос­кость рас­про­стра­не­ния яв­ля­ет­ся плос­ко­стью сим­мет­рии, та­кой мо­дой ока­зы­ва­ет­ся ло­ка­ли­зо­ван­ная SH-вол­на. В об­щем слу­чае на сво­бод­ной по­верх­но­сти пье­зо­элек­три­ка, в за­ви­си­мо­сти от элек­трич. гра­нич­ных ус­ло­вий, воз­мож­ны ли­бо од­на, ли­бо две по­верх­но­ст­ные вол­ны (Е. Ло­те, Д. Бар­нетт, 1976).

На пло­ской гра­ни­це раз­де­ла двух кри­стал­лич. сред мо­жет рас­про­стра­нять­ся ло­ка­ли­зо­ван­ная вол­на, ана­ло­гич­ная вол­не Сто­ун­ли на гра­ни­це ме­ж­ду дву­мя изо­троп­ны­ми по­лу­про­стран­ст­ва­ми. В от­личие от по­верх­но­ст­ных волн, су­ще­ст­во­ва­ние волн Сто­ун­ли не обя­за­тель­но, при этом в ка­ж­дом на­прав­ле­нии не мо­жет рас­про­стра­нять­ся бо­лее од­ной та­кой вол­ны. Ес­ли па­ра­мет­ры сре­ды до­пус­ка­ют су­ще­ст­во­ва­ние вол­ны Сто­ун­ли, то она долж­на со­хра­нить­ся в не­ко­то­ром ин­тер­ва­ле из­ме­не­ния этих па­ра­мет­ров (Д. Бар­нетт и др., 1985).

Во всех рас­смот­рен­ных вы­ше слу­ча­ях ско­ро­сти волн не за­ви­сят от час­то­ты (без­дис­пер­си­он­ные вол­ны). Од­на­ко дис­пер­сия волн воз­ни­ка­ет, как толь­ко по­яв­ля­ет­ся ко­неч­ный раз­мер сре­ды хо­тя бы в од­ном на­прав­ле­нии (напр., Лэм­ба вол­ны в пла­сти­не и Ля­ва вол­ны в струк­ту­ре «слой на под­лож­ке»). Ха­рак­тер­но, что тео­рии та­ких волн при­ме­ни­тель­но к кри­стал­лам поя­ви­лись лишь в нач. 21 в. Раз­ра­бот­ка этих тео­рий бы­ла вы­зва­на прак­тич. за­про­са­ми, по­сколь­ку аку­сто­элек­трон­ные уст­рой­ст­ва на вол­нах та­ких ти­пов уже ра­бо­та­ют. Это от­но­сит­ся и к раз­ви­вае­мым в по­след­ние го­ды тео­ри­ям аку­стич. волн в мно­го­слой­ных ани­зо­троп­ных струк­ту­рах [В. И. Аль­шиц, Ж. А. Мо­жен (Фран­ция), 2005].