КОГЕРЕ́НТНОСТЬ СВЕ́ТА
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
КОГЕРЕ́НТНОСТЬ СВЕ́ТА, взаимная согласованность протекания во времени световых колебаний в разных точках пространства и/или времени, характеризующая их способность к интерференции. Когерентность измеряется степенью взаимной когерентности, которая определяет контраст интерференционной картины в том или ином интерференционном эксперименте. Напр., в классич. опыте Юнга протяжённый источник света освещает экран $A$. Выделяя малыми отверстиями 1 и 2 два участка светового поля, можно исследовать распределение освещённости на удалённом экране $B$. Интенсивность света $I$ в некоторой точке $Q$ экрана $B$ в типичном случае квазимонохроматич. источника (ширина спектра $\Delta\nu$ мала по сравнению со ср. частотой $\nu$) даётся выражением $$I=I_1+I_2+2\sqrt {I_1I_2}|\gamma_{12}(\tau)|\text{cos} (2 \pi \nu \tau +\varphi). \tag 1 $$
Здесь $I_1 \ и\ I_2 $ – ср. интенсивности в точке $Q $ при освещении экрана $B$ порознь через отверстия 1 и 2; $|γ_{12}(τ)|$ – степень взаимной когерентности, являющаяся функцией расстояния между отверстиями 1 и 2 и разности времени $τ$ распространения света от точек 1 и 2 до точки $Q$; $\varphi$ – постоянная фаза, зависящая от положения отверстий 1 и 2 относительно источника. В частном случае $I_1=I_2 $ степень взаимной когерентности определяется через макс. и соседнее миним. значения интенсивностей в интерференционной картине:$$|\gamma_{12}(\tau)|=\frac{I_{макс}-I_{мин}}{I_{макс}+I_{мин}}.\tag 2 $$
Степень взаимной когерентности колебаний в двух точках поля может быть вычислена аналитически, если известны спектр излучения, распределение интенсивностей и относительные фазы элементарных излучателей источника света. Это эквивалентно нахождению функции корреляции $G_{12}(\tau)=〈V_1(t) \cdotp V_2^* (t+\tau)〉$световых полей $V_{1,2} (t)$ в точках 1 и 2, взятых в моменты времени $t\ и \ t+τ$. Угловые скобки означают усреднение по времени, звёздочка – сопряжение амплитуды $V $ поля, представленной в комплексной форме. При этом
$$|\gamma_{12}(t)|=\frac{|G_{12}(\tau)|}{\langle|V_1(t)|\rangle \langle|V_2(t)|\rangle}.\tag 3 $$
По мере взаимного удаления точек 1 и 2 корреляция между $V_1\ и\ V_2 $ падает, т. к. поля элементарных излучателей для точек 1 и 2 суммируются теперь с разл. амплитудами и фазами из-за разности расстояний до этих точек. Различие во временах также приводит к снижению корреляции ввиду конечной ширины спектра излучения.
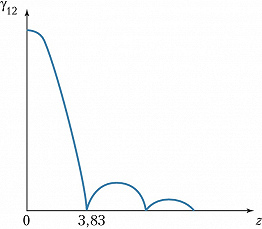
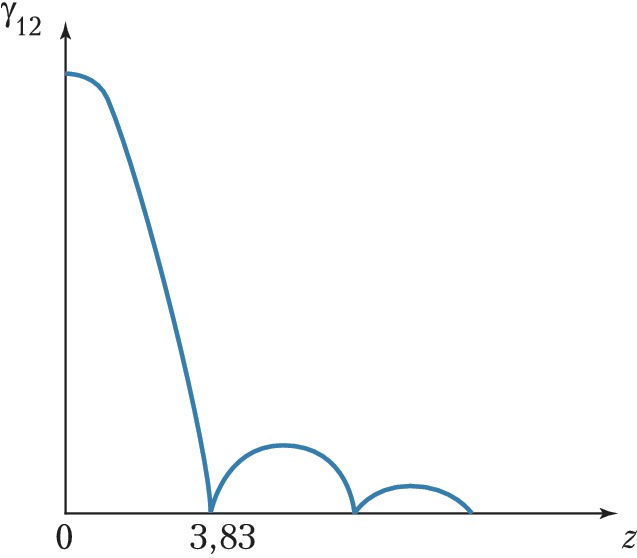
В случае небольших угловых размеров источника света вместо пространственно-временнóй когерентности можно рассматривать две – пространственную когерентность $|\gamma_{12}(0)|\equiv \gamma_{12}$ и временнýю когерентность $|\gamma_{11}(τ)|\equiv \gamma(\tau)$ с характерными параметрами – площадью когерентности $S_0 $ и временем когерентности $\tau_0$. Площадь когерентности – площадь $S_0$ на плоскости, перпендикулярной направлению на источник, ограниченная кривой, в пределах которой степень взаимной когерентности между любыми двумя точками не падает ниже некоторой заданной величины $γ_{12}^{мин}$. Для удалённого квазимонохроматич. источника, все элементы которого излучают независимо, $γ_{12}$ даётся пространственным Фурье преобразованием от распределения интенсивностей по площади источника. Напр., для источника в виде плоского диска постоянной светимости $\gamma_{12}= |2J_1(z)/z|$, где $J_1 $ – функция Бесселя 1-го рода, $z=\alpha r/\lambda$, $\lambda$ – длина волны, $\alpha$ – угловой размер источника; $r$ – расстояние между точками 1 и 2. График $\gamma_{12}$($z$) приведён на рис. Площади когерентности при освещении обычными источниками, как правило, очень малы. Напр., в солнечном свете степень взаимной когерентности обращается в нуль уже для точек, удалённых друг от друга на 3·10–3 см, что и определяет трудности наблюдения интерференции в экспериментах типа опыта Юнга. По мере уменьшения углового размера источника площадь когерентности растёт. На измерении функции $\gamma_{12}(z)$ основан метод Майкельсона определения диаметра звёзд (см. Звёздный интерферометр). Для лазеров площадь когерентности может перекрывать всё сечение пучка. В этом случае высокая степень взаимной когерентности является следствием вынужденного (следовательно, согласованного) характера испускания света частицами его рабочей среды в резонаторе, выделяющем типы колебаний малой угловой расходимости.
Временем когерентности $\tau_0 $ называется миним. задержка $\tau$ между интерферирующими световыми волнами, снижающая $\gamma(\tau)$ до заданной малой величины, напр. до 0. Зависимость $\gamma(\tau) $ даётся преобразованием Фурье от спектра мощности поля. Для поля с шириной спектра $\Delta \nu$ время когерентности $\tau_0 \approx 1/4 \pi \Delta \nu$. Для разл. источников света $\tau_0 $ меняется в широких пределах. Напр., для солнечного света $\tau_0 $ порядка 10–15 с, чему соответствует длина когерентности $\delta_0=c \tau_0$ ( $c$– скорость света$)$ порядка доли микрометра. Для узких спектральных линий газоразрядных источников света $\delta_0 $ доходит до десятков см. Для одночастотных лазеров $\tau_0 $ может доходить до долей секунды и, соответственно, $\delta_0 $ измеряется многими тысячами км. Если световое поле содержит неск. раздельных спектральных линий, то $\gamma(\tau) $является немонотонно убывающей функцией $\tau$. Напр., если спектр состоит из двух линий $\nu_1$ и $\nu_2$, то $\gamma(\tau)$ периодична с периодом $ (\nu_1-\nu_2)^{–1}$. Это характерно для лазерных источников.
Строго говоря, взаимно когерентны только поля, полученные от общего источника. Поля независимых источников некогерентны. Однако поля независимых источников с очень узкими спектральными линиями при наложении обнаруживают нестационарную интерференцию – биения (см. Интерференция света), если наблюдение проводится в течение времени $\Delta t≪\Delta \nu^{–1}$, $(\nu_1-\nu_2)^{–1}$ где $\nu_1 $ и $\nu_2$ – ср. частоты полей источников, $\Delta \nu$ – бóльшая из ширин линий $\nu_1$ и $\nu_2$. Понятие К. с. можно использовать в случае нестационарной интерференции, имея в виду в формуле $(3)$ усреднение по интервалу времени $\Delta \tau$. Нестационарная интерференция наблюдается только при достаточно высокой яркости источников света, когда в объёме когерентности $V_0=S_0\tau_0 $ число фотонов не малó по сравнению с единицей. Практически нестационарная интерференция имеет место только для лазерных источников.