ЗО́ННЫЙ МАГНЕТИ́ЗМ

ЗО́ННЫЙ МАГНЕТИ́ЗМ, маг­не­тизм ме­тал­лов, их спла­вов и со­еди­не­ний, ин­тер­пре­ти­руе­мый в рам­ках мо­де­лей, ос­но­ван­ных на зон­ной тео­рии

. Та­кие ве­ще­ст­ва на­зы­ва­ют­ся зон­ны­ми маг­не­ти­ка­ми; их ти­пич­ные пред­ста­ви­те­ли – пе­ре­ход­ные ме­тал­лы $\ce{Fe, Co, Ni, Сr, Мn}$, их спла­вы и со­еди­не­ния.

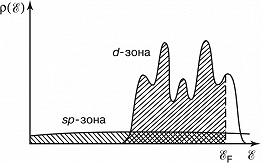
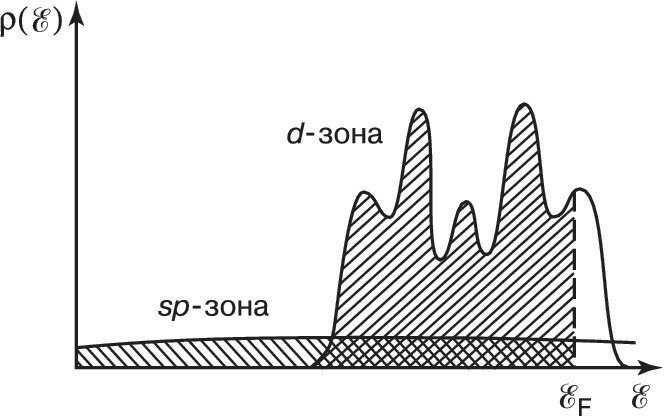
Энер­ге­тич. спектр пе­ре­ход­ных ме­тал­лов пред­став­ля­ет со­бой ши­ро­кую $sp$-зо­ну (об­ра­зо­ван­ную энер­ге­тич. уров­ня­ми $s$- и $p$-элек­т­ро­нов), в ко­то­рую по­гру­же­на сис­те­ма пя­ти уз­ких пе­ре­се­каю­щих­ся $d$-зон (со­во­куп­но­сти энер­ге­тич. уров­ней $d$-элект­ро­нов) (рис. 1). По срав­не­нию с ти­пич­ны­ми зо­на­ми про­во­ди­мо­сти $s$- и $p$-элек­тро­нов $d$-зо­ны име­ют мень­шую ши­ри­ну, но плот­ность энер­ге­тич. уров­ней в них ока­зы­ва­ет­ся го­раз­до вы­ше плот­но­сти уров­ней $s$- и $p$-элек­тро­нов в той же об­лас­ти энер­гий, где рас­по­ложе­ны $d$-зо­ны. Об этом сви­де­тель­ст­ву­ет су­ще­ст­вен­ный вклад $d$-элек­тро­нов в низ­ко­тем­пе­ра­тур­ную те­п­ло­ём­кость $С_{эл} = γT$, где $γ$ про­пор­цио­наль­на $ρ(ℰ_F)$, т. е. зна­че­нию плот­но­сти со­стоя­ний на фер­ми-уров­не $ℰ_F$. Ко­эф. γ пе­ре­ход­ных ме­тал­лов на по­ря­док боль­ше, чем др. ме­тал­лов; $d$-элек­тро­ны пе­ре­ход­ных ме­тал­лов по сво­им свой­ст­вам за­ни­ма­ют про­ме­жу­точ­ное по­ло­же­ние ме­ж­ду ло­ка­ли­зо­ван­ны­ми и кол­лек­ти­ви­зи­ро­ван­ны­ми элек­тро­на­ми. Оцен­ки энер­гии свя­зи элек­тро­нов в кри­стал­ле и ис­сле­до­ва­ние фер­ми-по­верх­но­стей сви­де­тель­ст­ву­ют о зна­чит. сте­пе­ни кол­лек­ти­ви­зации $d$-элек­тро­нов. Так, ср. маг­нит­ные мо­мен­ты на атом, из­ме­рен­ные в $μ_Б \;(μ_Б$ – маг­не­тон Бо­ра), пе­ре­ход­ных ме­тал­лов яв­ля­ют­ся дроб­ны­ми, в то вре­мя как маг­нит­ные мо­мен­ты изо­ли­ро­ван­ных ато­мов – це­лые чис­ла; кро­ме то­го, из­ме­рен­ное зна­че­ние $g$-фак­то­ра пе­ре­ход­ных ме­тал­лов близ­ко к 2 (зна­че­ние $g$ = 2 от­ве­ча­ет мо­де­ли сво­бод­ных элек­тро­нов). Напр., маг­нит­ный мо­мент $\ce{Ni}$ со­став­ля­ет 0,583$μ_Б$, $\ce{Fe}$ – 2,177$μ_Б$, $\ce{Co}$ – 1,707$μ_Б$; дроб­ность зна­че­ния маг­нит­но­го мо­мен­та сви­де­тель­ст­ву­ет о том, что спон­тан­ная на­маг­ни­чен­ность в этих ме­тал­лах соз­да­ёт­ся кол­лек­ти­ви­зи­ро­ван­ны­ми элек­тро­на­ми. Рас­сея­ние мед­лен­ных ней­тро­нов на спи­но­вых вол­нах

в этих ве­ще­ст­вах хо­ро­шо опи­сы­ва­ет­ся как в рам­ках мо­де­ли Гей­зен­бер­га, ос­но­ван­ной на пред­став­ле­нии о ло­ка­ли­зо­ван­ных маг­нит­ных мо­мен­тах, так и в рам­ках мо­де­ли кол­лек­ти­ви­зи­ро­ван­ных элек­тро­нов.

Рас­пре­де­ле­ние за­ря­до­вой плот­но­сти в фер­ро­маг­нит­ных ме­тал­лах ($\ce{Fe, Ni, Co}$) близ­ко к атом­но­му. Двой­ст­вен­ный ха­рак­тер по­ве­де­ния $d$-элек­тро­нов обу­слов­лен тем, что пе­ре­кры­тие $d$-ор­би­та­лей со­сед­них ато­мов в пе­ре­ход­ных ме­тал­лах ока­зы­ва­ет­ся зна­чи­тель­ным, и элек­тро­ны име­ют воз­мож­ность пе­ре­ме­щать­ся по все­му об­раз­цу. В ре­зуль­та­те атом­ный $d$-уро­вень уши­ря­ет­ся и об­ра­зу­ет­ся $d$-зо­на. Ме­ж­ду $d$-элек­тро­на­ми су­ще­ст­ву­ет ку­ло­нов­ское взаи­мо­дей­ст­вие. Наи­боль­ший вклад в энер­гию взаи­мо­дей­ст­вия $U$ вно­сит ку­ло­нов­ское от­тал­ки­ва­ние элек­тро­нов с про­ти­во­по­лож­ны­ми на­прав­ле­ния­ми про­ек­ции спи­на, на­хо­дя­щих­ся вбли­зи од­но­го и то­го же уз­ла кри­стал­лич. ре­шёт­ки.

Оцен­ки по­ка­зы­ва­ют, что для двух элек­тро­нов, на­хо­дя­щих­ся на рас­стоя­нии $r$ по­ряд­ка ра­диу­са Бо­ра, энер­гия $U$ по­ряд­ка 10 эВ. Для элек­тро­нов, ло­ка­ли­зо­ван­ных на со­сед­них уз­лах ре­шёт­ки, энер­гия $U$ на по­ря­док мень­ше. Наи­бо­лее су­ще­ст­вен­ным для по­яв­ле­ния маг­нит­но­го по­ряд­ка в пе­ре­ход­ных ме­тал­лах яв­ля­ет­ся то, что энер­гия $U$ в этих ме­тал­лах боль­ше ши­ри­ны $d$-зо­ны ($U ⩾ W$, где $W$ по­ряд­ка 1 эВ – ши­ри­на $d$-зо­ны). В этом слу­чае ку­ло­нов­ское ме­жэ­лек­трон­ное взаи­мо­дей­ст­вие су­ще­ст­вен­но влия­ет на дви­же­ние $d$-элек­тро­нов и в си­лу это­го ра­ди­каль­но ме­ня­ет их плот­ность со­стоя­ний. Имен­но это взаи­мо­дей­ст­вие при­во­дит к раз­движ­ке энер­ге­тич. зон элек­тро­нов с разл. на­прав­ле­ния­ми спи­на и воз­ник­но­ве­нию спон­тан­ной на­маг­ни­чен­но­сти.

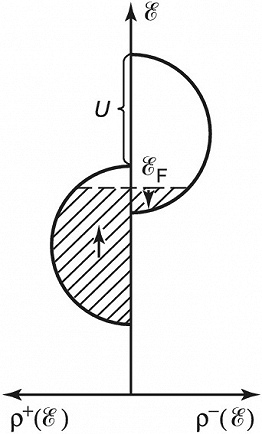
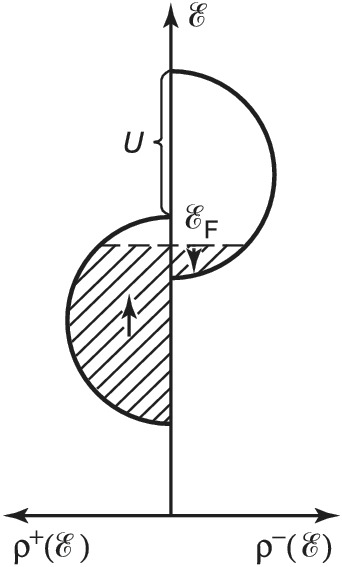
Для то­го что­бы сис­те­ма кол­лек­ти­ви­зи­ро­ван­ных элек­тро­нов об­ла­да­ла на­маг­ни­чен­но­стью, не­об­хо­ди­мо, что­бы под­зо­ны элек­тро­нов с про­ек­ция­ми спи­нов +¹/₂ и –¹/₂ бы­ли по-раз­но­му за­пол­не­ны. В рам­ках т. н. мо­де­ли Сто­не­ра это дос­ти­га­ет­ся про­стей­шим спо­со­бом: пред­по­ла­га­ет­ся, что ку­ло­нов­ское взаи­мо­дей­ст­вие ме­ж­ду элек­тро­на­ми при­во­дит лишь к раз­движ­ке под­зон элек­тро­нов с раз­ны­ми про­ек­ция­ми спи­на, при­чём за­кон дис­пер­сии и плот­ность со­стоя­ний не из­ме­ня­ют­ся. Схе­ма­ти­че­ски это изо­бра­же­но на рис. 2.

На­маг­ни­чен­ность $m$ сис­те­мы $d$-элек­тро­нов оп­ре­де­ля­ет­ся раз­но­стью чис­ла элек­тро­нов с ори­ен­та­ци­ей спи­нов по на­маг­ни­чен­но­сти и чис­ла элек­тро­нов с ори­ен­та­ци­ей спи­нов про­тив на­маг­ни­чен­но­сти. В ре­зуль­та­те мож­но за­пи­сать урав­не­ние, оп­ре­де­ляю­щее ве­ли­чи­ну сум­мар­но­го маг­нит­но­го мо­мен­та $m\; d$-элек­тро­нов ме­тал­ла при лю­бой темп-ре. Сре­ди его ре­ше­ний все­гда име­ет­ся три­ви­аль­ное ре­ше­ние $m = 0$, а темп-pa, при ко­то­рой по­яв­ля­ет­ся не­три­ви­аль­ное ре­ше­ние $m ≠ 0$, пред­став­ля­ет со­бой темп-ру Кю­ри $T_C$ в дан­ной мо­де­ли. Зна­че­ние $T_C$ оп­ре­де­ля­ют из урав­не­ния, ко­то­рое по­лу­ча­ет­ся при диф­фе­рен­ци­ро­ва­нии ле­вой и пра­вой час­тей урав­не­ния для маг­нит­ного мо­мен­та по $m$ в точ­ке $m = 0$. Су­ще­ст­во­ва­ние фер­ро­маг­не­тиз­ма воз­мож­но, ес­ли $T_C$ > 0. По­ла­гая $T_C = 0$, по­лу­чим кри­тич. ус­ло­вие воз­ник­но­ве­ния фер­ро­маг­не­тиз­ма в дан­ной мо­де­ли – кри­те­рий Сто­не­ра: $U\!ρ(ℰ_F) > 1$, где $ρ(ℰ_F)$ – зна­че­ние плот­но­сти элек­трон­ных со­стоя­ний на фер­ми-уров­не. Как вид­но из это­го ус­ло­вия, для воз­ник­но­ве­ния фер­ро­маг­не­тиз­ма в мо­де­ли Сто­не­ра не­об­хо­ди­мо, что­бы дос­та­точ­но боль­ши­ми бы­ли как энер­гия взаи­мо­дей­ст­вия $d$-элек­тро­нов, так и плот­ность со­стоя­ний на уров­не Фер­ми. Т. о., уже для са­мой про­стой мо­де­ли фер­ро­маг­нит­но­го ме­тал­ла ока­зы­ва­ет­ся, что темп-pa пе­ре­хо­да и са­мо су­ще­ст­во­ва­ние фер­ро­маг­нит­но­го со­стоя­ния оп­ре­де­ля­ют­ся струк­ту­рой энер­ге­тич. зон элек­тро­нов, зна­че­ни­ем плот­но­сти со­стоя­ний вбли­зи по­верх­но­сти Фер­ми и раз­движ­кой под­зон элек­тро­нов с разл. про­ек­ци­ей спи­на.

Струк­ту­ра энер­ге­тич. зон оп­ре­де­ля­ет и осн. со­стоя­ние, и рав­но­вес­ные тер­мо­ди­на­мич. свой­ст­ва сис­те­мы, та­кие, напр., как за­ви­си­мость маг­нит­но­го мо­мен­та от темп-ры. До­пол­нит. вклад в тер­мо­ди­на­мич. ха­рак­те­ри­сти­ки да­ют кол­лек­тив­ные воз­бу­ж­де­ния ти­па спи­но­вых волн. Для ко­ли­че­ст­вен­но­го рас­чё­та свойств зон­ных маг­не­ти­ков в осн. со­стоя­нии при­ме­ня­ет­ся ме­тод функ­цио­на­ла спи­но­вой плот­но­сти. В рам­ках это­го под­хо­да точ­ный га­миль­то­ни­ан сис­те­мы взаи­мо­дей­ст­вую­щих элек­тро­нов за­ме­ня­ет­ся га­миль­то­ниа­ном га­за не­взаи­мо­дей­ст­вую­щих час­тиц в эф­фек­тив­ном не­ло­каль­ном по­тен­циа­ле. В при­бли­же­нии ло­каль­ной спи­но­вой плот­но­сти уда­ёт­ся по­ка­зать, что кри­те­рий Сто­не­ра спра­вед­лив толь­ко для фер­ро­маг­нит­ных пе­ре­ход­ных ме­тал­лов $\ce{Fe, Co, Ni}$ (при $T = 0$). Од­на­ко при ко­неч­ных темп-pax свой­ст­ва зон­ных маг­не­ти­ков опи­сать на ос­но­ве тео­рии Сто­не­ра не уда­ёт­ся. В рам­ках этой тео­рии не­воз­мож­но со­гла­со­вать боль­шие (по­ряд­ка 1 эВ) зна­че­ния энер­гии меж­зон­но­го рас­ще­п­ле­ния, не­об­хо­ди­мые для соз­да­ния экс­пе­ри­мен­таль­но из­ме­ряе­мо­го маг­нит­но­го мо­мен­та на­сы­ще­ния, и низ­кие (по­ряд­ка 1000 К) зна­че­ния темп-ры Кю­ри пе­ре­ход­ных ме­тал­лов. Кро­ме то­го, не уда­ёт­ся объ­яс­нить на­блю­дае­мое экс­пе­ри­мен­таль­но по­ве­де­ние вос­при­им­чи­во­сти при темп-pax вы­ше $T_C$, сле­дую­щее Кю­ри – Вей­са за­ко­ну

. Слиш­ком вы­со­кое по срав­не­нию с экс­пе­ри­мен­таль­ным зна­че­ние темп-ры Кю­ри, по­лу­чае­мое в рам­ках тео­рии Сто­не­ра, сви­де­тель­ст­ву­ет о том, что осн. фер­ро­маг­нит­ное со­стоя­ние раз­ру­ша­ет­ся не сто­не­ров­ски­ми воз­бу­ж­де­ния­ми (т. е. воз­бу­ж­де­ния­ми, соз­да­вае­мы­ми при пе­ре­хо­де од­но­го элек­тро­на из зо­ны с ори­ен­та­ци­ей спи­на +¹/₂ в зо­ну с ори­ен­та­ци­ей спи­на –¹/₂), а кол­лек­тив­ны­ми флук­туа­ция­ми спи­но­вой плот­но­сти.

Япон. фи­зик Т. Мо­рия с со­ав­то­ра­ми раз­вил тео­рию спи­но­вых флук­туа­ций, за­ме­нив сис­те­му взаи­мо­дей­ст­вую­щих спи­нов сис­те­мой не­взаи­мо­дей­ст­вую­щих спи­нов в про­из­воль­но флук­туи­рую­щих по­лях. Рас­счи­тан­ное в рам­ках этой тео­рии зна­че­ние темп-ры Кю­ри хо­тя и вы­ше экс­пе­ри­мен­таль­но­го зна­че­ния, но зна­чи­тель­но ни­же рас­счи­тан­но­го в рам­ках тео­рии Сто­не­ра.

В зон­ных маг­не­ти­ках мо­жет воз­ни­кать не толь­ко фер­ро­маг­нит­ный по­ря­док. Экс­пе­ри­мен­ты по рас­сея­нию ней­тро­нов в $\ce{Cr}$, $α$-фа­зе $\ce{Mn}$ и $γ$-фа­зе $\ce{Fe}$ по­ка­зы­ва­ют, что в спек­трах рас­сея­ния воз­ни­ка­ет ряд пи­ков, сви­де­тель­ст­вую­щих о су­ще­ст­во­ва­нии в этих ма­те­риа­лах ан­ти­фер­ро­маг­нит­но­го упо­ря­до­че­ния (см. Ан­ти­фер­ро­маг­не­тизм

). Наи­бо­лее ин­те­ре­сен с точ­ки зре­ния маг­не­тиз­ма кол­лек­ти­ви­зи­ро­ван­ных элек­тро­нов $\ce{Cr}$, су­ще­ст­вен­но от­ли­чаю­щий­ся от обыч­ных ан­ти­фер­ро­маг­не­ти­ков. Во-пер­вых, в чис­том $\ce{Cr}$ дли­на вол­ны спи­но­вой плот­но­сти (см. Спи­но­вой плот­но­сти вол­ны

 >>

) не­со­из­ме­ри­ма с пе­рио­дом кри­стал­лич. ре­шёт­ки. Вол­но­вой век­тор этой струк­ту­ры на­прав­лен вдоль од­ной из осей ти­па [100] и сла­бо за­ви­сит от темп-ры. Во-вто­рых, вы­ше Не­еля точ­ки

 >>

($T_N$ = 312 К) не су­ще­ст­ву­ет ло­ка­ли­зо­ван­ных маг­нит­ных мо­мен­тов. Ср. маг­нит­ный мо­мент на атом $\ce{Cr}$ ра­вен 0,46$μ_Б$. При 120 К в $\ce{Cr}$ про­ис­хо­дит маг­нит­ный фа­зо­вый пе­ре­ход

 >>

(спин-флип пе­ре­ход

 >>

с пе­ре­ори­ен­та­ци­ей маг­нит­ных мо­мен­тов).