СПИРА́ЛЬ

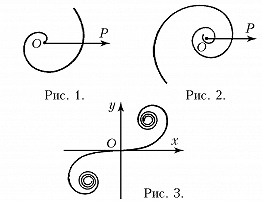
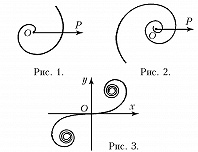
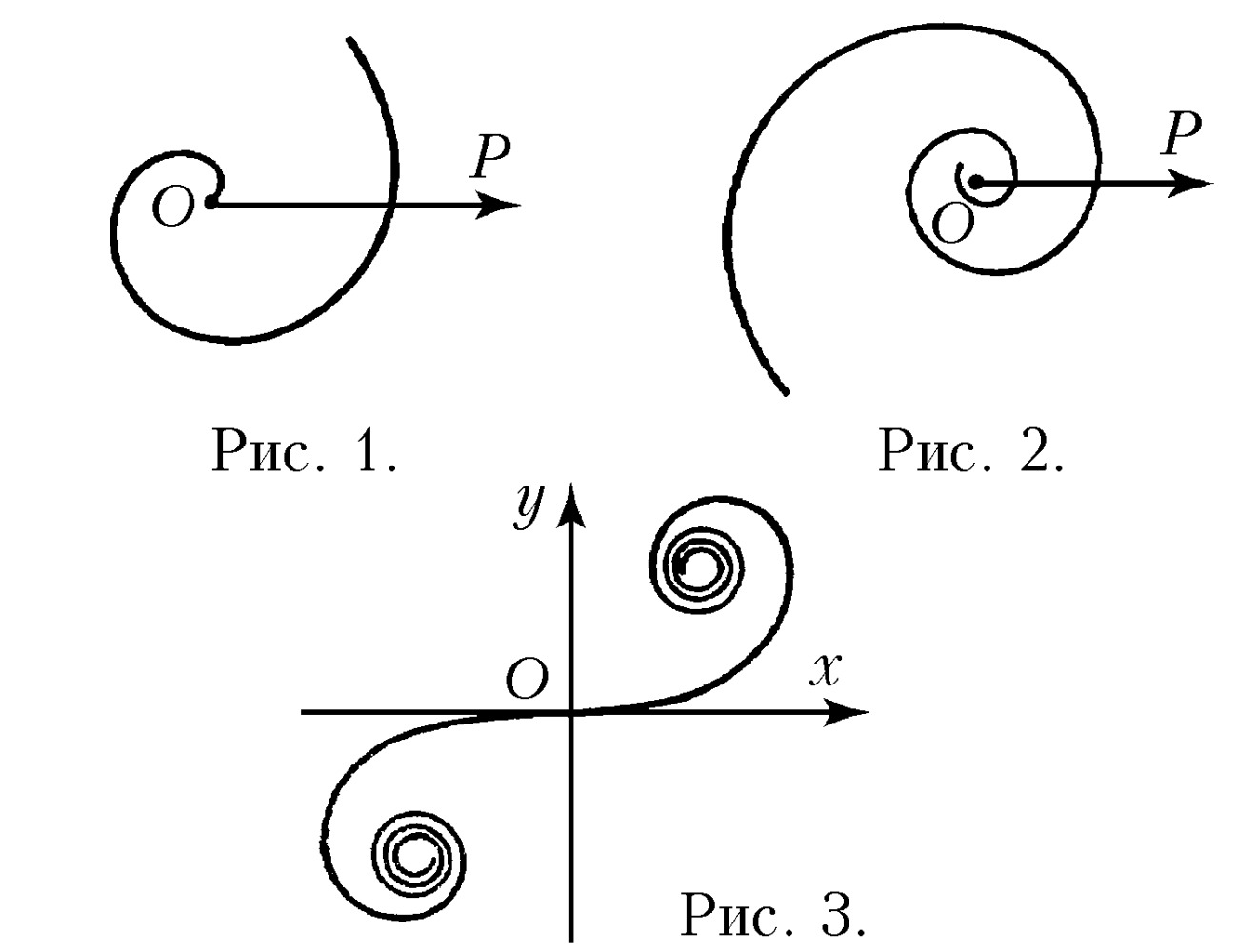
СПИРА́ЛЬ (франц. spirale, от лат. spira, от греч. σπεῖρα – из­гиб, ви­ток), пло­ская кри­вая, ко­то­рая об­хо­дит не­ко­то­рую точ­ку, с ка­ж­дым об­хо­дом при­бли­жа­ясь к ней или с ка­ж­дым об­хо­дом уда­ля­ясь от неё. Ес­ли вы­брать эту точ­ку за по­люс по­ляр­ной сис­те­мы ко­ор­ди­нат, то по­ляр­ное урав­не­ние С. $ρ=f(φ)$, где $f(φ+2π) < f(φ)$ или $f(φ+2π) > f(φ)$ при всех $φ$. В ча­ст­но­сти, С. по­лу­ча­ет­ся, ес­ли $f(φ)$ – мо­нотон­но воз­рас­таю­щая или убы­ваю­щая по­ло­жи­тель­ная функ­ция. Наи­бо­лее про­стой вид име­ет урав­не­ние ар­хи­ме­до­вой С. (рис. 1) $ρ=aφ$, $a > 0$, $φ ⩾ 0$, изу­чав­шей­ся Ар­хи­ме­дом в свя­зи с за­да­ча­ми три­сек­ции уг­ла и квад­ра­ту­ры кру­га. Урав­не­ние $ρ=ae^{kφ}$, $a > 0$, за­да­ёт ло­га­риф­мич. С. (рис. 2), ко­то­рая пе­ре­се­ка­ет под од­ним и тем же уг­лом $α$ все лу­чи, ис­хо­дя­щие из по­лю­са, при этом $\text{ctg}\, α=k$. О ги­пер­бо­лич. С. см. в ст. Ли­ния. По­ми­мо С., ко­то­рые об­хо­дят од­ну точ­ку, встре­ча­ют­ся С., ко­то­рые об­хо­дят не­сколь­ко то­чек. При­мер та­кой С. да­ёт спи­раль Кор­ню (рис. 3), ко­то­рая ис­поль­зо­ва­лась франц. фи­зи­ком М. Кор­ню (1874) для ре­ше­ния не­ко­то­рых за­дач ди­фрак­ции све­та. Па­ра­мет­рич. урав­не­ния этой С. в де­кар­то­вых ко­ор­ди­на­тах име­ют вид $$x=\int_0^t \cos \frac{\pi u^2}{2} du, \\ y=a \int_0^t \sin \frac{\pi u^2}{2} du.$$