ТРАКТРИ́СА

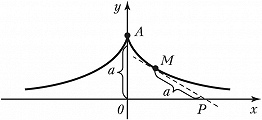
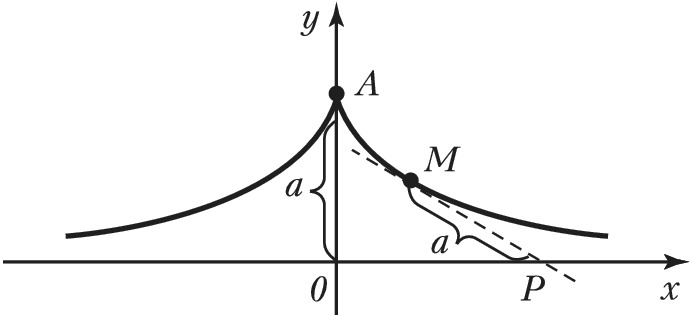
ТРАКТРИ́СА (но­во­ла­тин­ское tractrix, от лат. tractus – вы­тя­ну­тый), пло­ская транс­цен­дент­ная кри­вая, для ко­то­рой дли­на от­рез­ка ка­са­тель­ной в дан­ной точ­ке от этой точ­ки до оси абс­цисс по­сто­ян­на. На рис. по­ка­зан от­ре­зок ка­са­тель­ной к Т. в точ­ке $M$ от точ­ки $M$ до точ­ки $P$ её пе­ре­се­че­ния с осью абс­цисс; дли­на от­рез­ка $MP$ для всех то­чек $M$ рав­на $a$. Урав­не­ние Т. в пря­мо­уголь­ных ко­ор­ди­на­тах:

$$x=\pm a \left( \ln \frac{a+\sqrt{a^2-y^2}}{y} - \sqrt{a^2-y^2} \right).$$ Т. сим­мет­рич­на от­но­си­тель­но оси $Oy$. Ось $O$x – асим­пто­та. Осо­бая точ­ка

 >>

 $A(0, a)$ – точ­ка воз­вра­та 1-го ро­да с вер­ти­каль­ной ка­са­тель­ной. Дли­на ду­ги $AM$ $$L=a\ln \frac{a}{y}.$$ Ра­ди­ус кри­виз­ны $$R=a\,\text{ctg}\frac{x}{y}.$$ Пло­щадь, ог­ра­ни­чен­ная Т. и её асим­пто­той, $$S=\frac{\pi a^2}{2}$$ Во­прос о фор­ме Т. впер­вые по­став­лен К. Пер­ро

 >>

(1675). Кри­вая ис­сле­до­ва­на Г. В. Лейб­ни­цем

 >>

и Х. Гюй­ген­сом

 >>

.