СОПРИКОСНОВЕ́НИЕ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
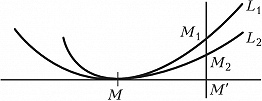
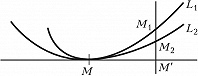
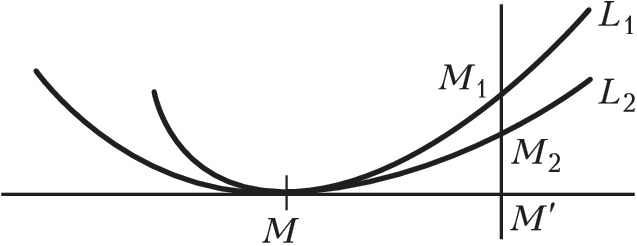
СОПРИКОСНОВЕ́НИЕ кривой L2 с кривой L1 в точке M, геометрич. понятие, означающее, что L2 имеет с L1 в точке M касание макс. порядка по сравнению с любой кривой из некоторого заранее данного семейства кривых {L2}, включающего L2. Порядок касания кривых L2 и L1 считается равным n, если отрезок M1M2 есть величина (n+1)-го порядка малости по отношению к отрезку MM´ (см. рис., где отрезок M2M1 перпендикулярен к общей касательной кривых L2 и L1 в точке M). Т. о., среди всех кривых семейства {L2} С. с кривой L1 имеет та кривая, которая наиболее тесно прилегает к L1 (для неё отрезок M2M1 имеет макс. порядок малости). Кривая семейства {L2}, которая имеет С. с кривой L1 в данной её точке M, называется соприкасающейся кривой данного семейства в указанной точке кривой L1. Напр., соприкасающейся окружностью в точке M кривой L1 является окружность, которая в этой точке имеет с L1 макс. порядок касания по сравнению с любой другой окружностью.
Аналогично определяется понятие соприкосновения поверхности S2, принадлежащей данному семейству поверхностей {S2}, с к.-л. кривой L1 (или с поверхностью S1) в некоторой её точке M (в этих случаях порядок касания определяется также аналогично предыдущему; следует только вместо касательной прямой MM´ рассматривать касательную плоскость поверхности S2 в точке M). См. также Соприкасающаяся плоскость, Соприкасающаяся сфера.