ПОДО́БИЕ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
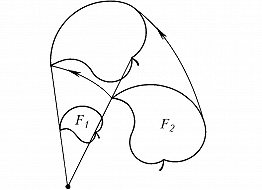
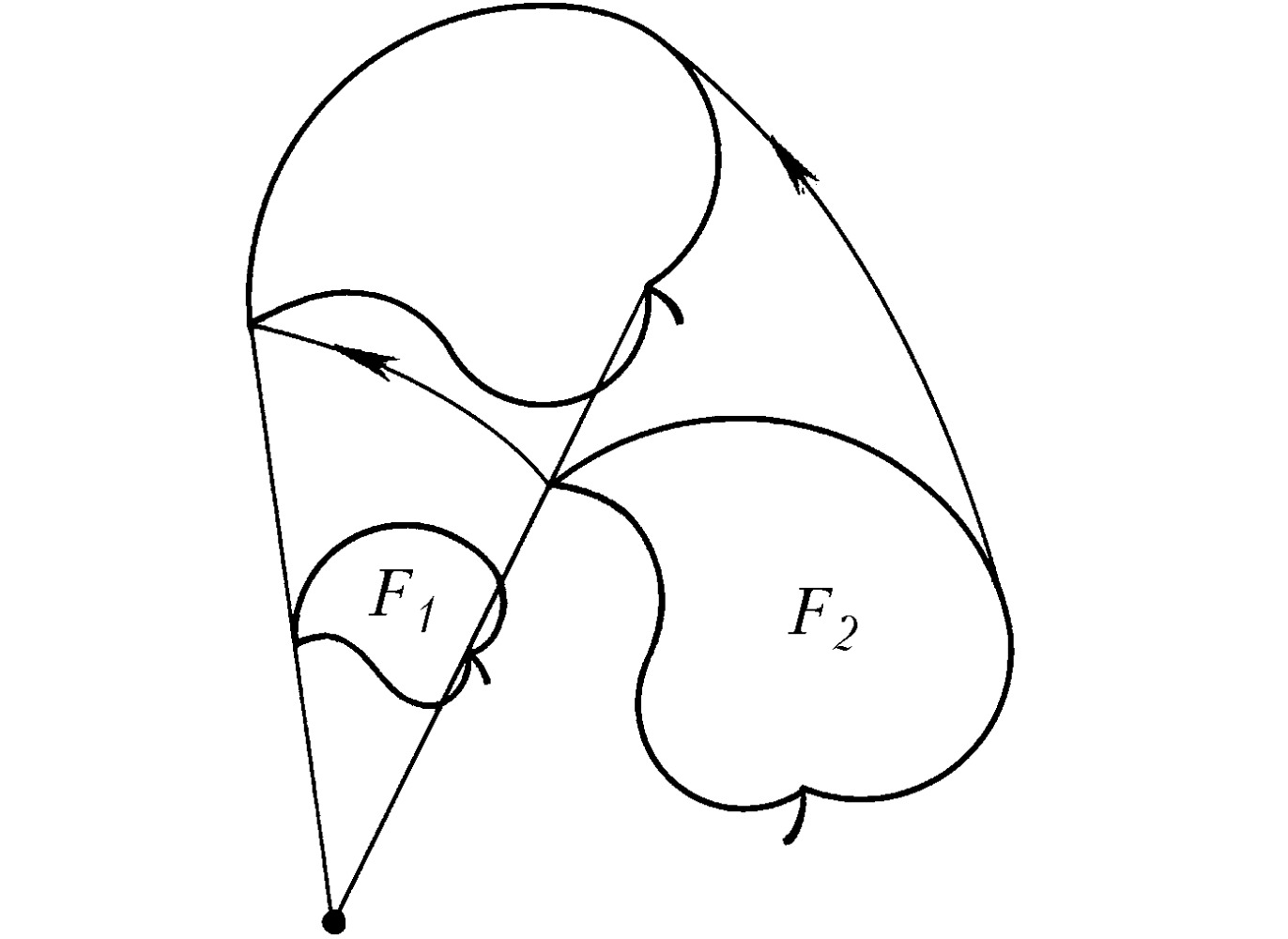
ПОДО́БИЕ в математике, понятие, означающее наличие у геометрич. фигур одинаковой формы, независимо от их размеров. Две фигуры, $F_1$ и $F_2$, называются подобными, если между их точками можно установить взаимно однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек равно одной и той же постоянной $k$, которая называется коэффициентом подобия. Углы между соответствующими линиями подобных фигур равны. Отношение площадей ограниченных подобных фигур равно квадрату коэффициента П., а отношение объёмов – его кубу.
Для П. треугольников необходимым и достаточным является каждый из следующих признаков: стороны одного пропорциональны сторонам другого; два угла одного равны двум углам другого; две стороны одного пропорциональны двум сторонам другого, а углы между этими сторонами равны; две стороны одного пропорциональны двум сторонам другого, а наибольший угол одного равен наибольшему углу другого.
Геометрич. преобразование плоскости, при котором все фигуры плоскости переходят в им подобные с одним и тем же коэффициентом П., называется преобразованием П. Преобразования П. образуют группу, они являются частным случаем аффинного преобразования. Всякое преобразование П. – результат (рис.) гомотетии и движения (собственного или несобственного).
Теория П. существенно связана с постулатом о параллельности, который эквивалентен существованию хотя бы одной пары неравных подобных треугольников. В геометрии Лобачевского из П. треугольников вытекает их равенство.