ГОМОТЕ́ТИЯ

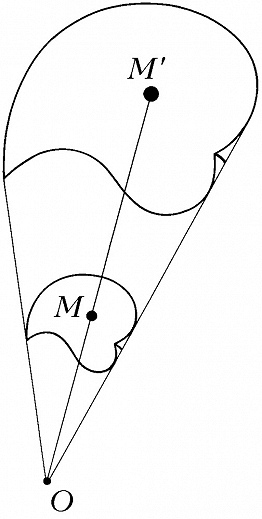
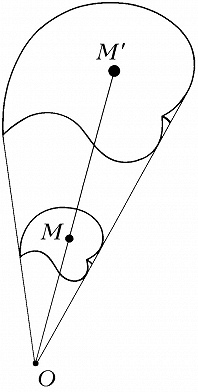
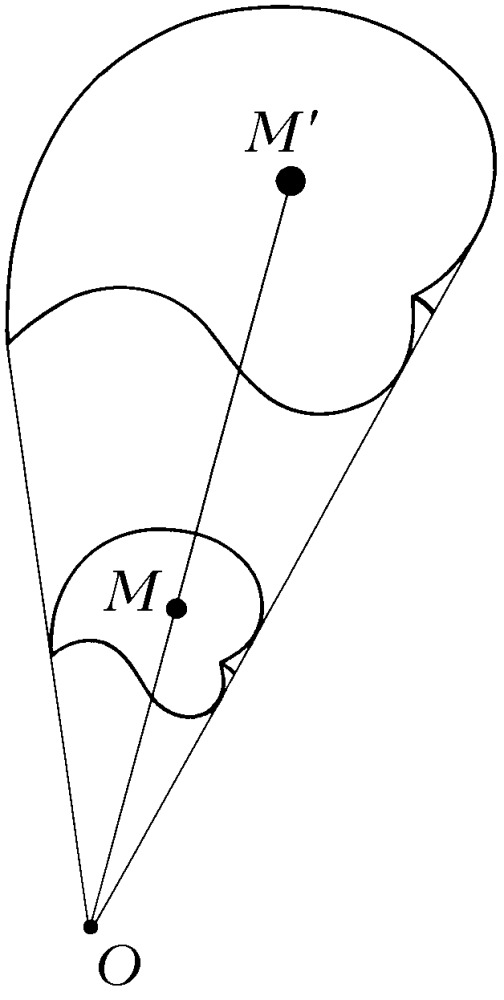
ГОМОТЕ́ТИЯ (от го­мо...

и греч. ϑετός – по­став­лен­ный, рас­по­ло­жен­ный), пре­об­ра­зо­ва­ние евк­ли­до­ва про­стран­ст­ва, ста­вя­щее в со­от­вет­ст­вие ка­ж­дой точ­ке $M$ точ­ку $M'$, ле­жа­щую на пря­мой $OM$, по пра­ви­лу $OM′=k·OM$, где $k$ – по­сто­ян­ное, от­лич­ное от ну­ля чис­ло, на­зы­вае­мое ко­эф­фи­ци­ен­том Г., $O$ – фик­си­ро­ван­ная точ­ка, центр Г. (рис.). При $k>0$ точ­ки $M$ и $M′$ ле­жат на од­ном лу­че по од­ну сто­ро­ну от цен­тра $O$; при $k<0$ точ­ки $M$ и $M′$ ле­жат по раз­ные сто­ро­ны от цен­тра, и Г. на­зы­ва­ет­ся об­рат­ной. При $k=1$ Г. есть то­ж­де­ст­вен­ное пре­об­ра­зо­ва­ние, при $k=–1$ – сим­мет­рия от­но­си­тель­но цен­тра. При Г. пря­мая пе­ре­хо­дит в пря­мую, со­хра­ня­ет­ся па­раллельность пря­мых и плос­ко­стей. Г. есть ча­ст­ный слу­чай по­до­бия

 >>

.

См. так­же Го­мо­ло­гия

в ма­те­ма­ти­ке.