ГОМОЛО́ГИЯ

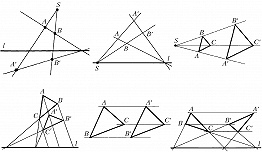
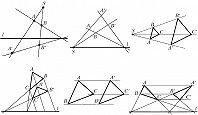
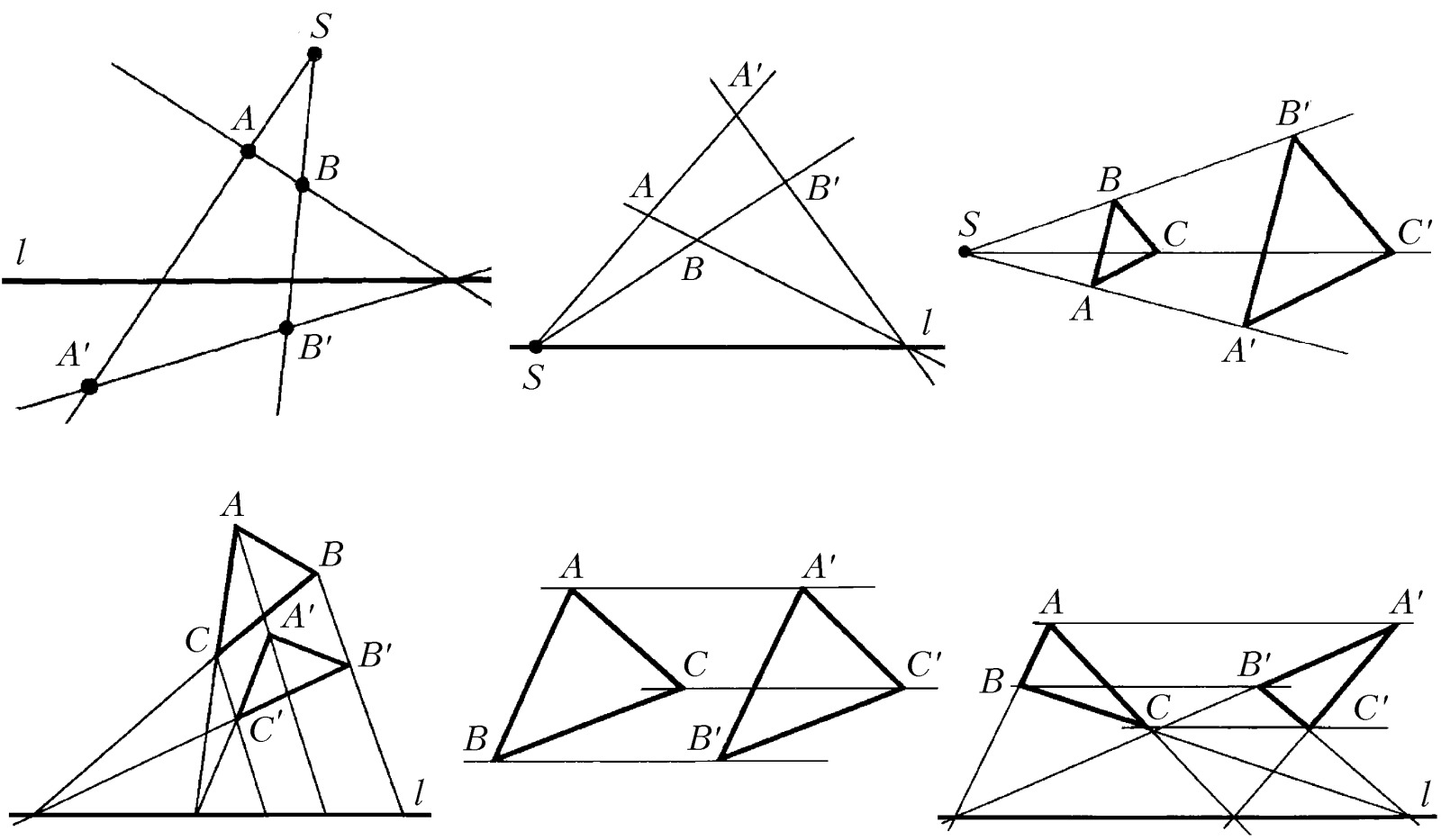
ГОМОЛО́ГИЯ в ма­те­ма­ти­ке, вза­им­но од­но­знач­ное про­ек­тив­ное пре­об­ра­зо­ва­ние про­ек­тив­ной плос­ко­сти в се­бя, пе­ре­во­дя­щее все точ­ки не­ко­то­рой пря­мой l (оси Г.) в се­бя и имею­щее ров­но од­ну не­под­виж­ную точ­ку $S$ (центр Г.). Ес­ли центр Г. не ле­жит на оси Г., то Г. на­зы­ва­ет­ся не­осо­бен­ной, или ги­пер­бо­ли­че­ской (рис. 1). Ес­ли центр Г. ле­жит на оси Г., то Г. на­зы­ва­ет­ся осо­бен­ной, или па­ра­бо­ли­че­ской (рис. 2). Г. с соб­ст­вен­ным (ко­неч­ным) цен­тром и не­соб­ст­вен­ной (бес­ко­неч­но уда­лён­ной) осью есть го­мо­те­тия (рис. 3). Г. с не­соб­ст­вен­ным цен­тром и соб­ст­вен­ной осью есть рас­тя­же­ние или сжа­тие к оси (рис. 4). Г. с не­соб­ст­вен­ной осью и не­соб­ст­вен­ным цен­тром – па­рал­лель­ный пе­ре­нос (рис. 5). Па­ра­бо­лич. Г. с бес­ко­неч­но уда­лён­ным цен­тром и соб­ст­вен­ной осью – сдвиг (рис. 6). На рис. 1–6 сим­во­ла­ми $A′, B′, C′$ от­ме­че­ны точ­ки, по­лу­чаю­щие­ся из то­чек $A, B, C$ при дей­ст­вии го­мо­ло­гии.

Вся­кое про­ек­тив­ное пре­об­ра­зо­ва­ние есть ре­зуль­тат по­сле­до­ва­тель­но­го при­ме­не­ния двух пре­об­ра­зо­ва­ний: Г. и дви­же­ния.