ПЛО́ЩАДЬ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
ПЛО́ЩАДЬ, одна из количественных характеристик, связанных с геометрич. фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины.
Вычисление П. уже в древности было одной из важнейших задач практич. геометрии, что связано с измерением земельных участков. За неск. столетий до н. э. греч. учёные располагали точными правилами вычисления П., которые в «Началах» Евклида облечены в форму теорем. При этом П. многоугольников определялись теми же приёмами разложения и дополнения фигур, которые сохранились в школьном преподавании. Для вычисления П. фигур с криволинейными границами применялся предельный переход в форме исчерпывания метода.
Теория П. плоских фигур, ограниченных простыми (т. е. не пересекающими себя) контурами, может быть построена следующим образом. Рассматриваются всевозможные многоугольники, вписанные в данную фигуру $F$, и всевозможные многоугольники, описанные вокруг фигуры $F$. (Вычисление П. многоугольника не представляет труда.) Пусть {$s$} – множество чисел, которые суть П. вписанных в фигуру многоугольников, а {$S$} – множество чисел, которые суть П. описанных вокруг фигуры многоугольников. Множество {$s$} ограничено сверху (площадью любого описанного многоугольника), а множество {$S$} ограничено снизу (напр., числом нуль). Наименьшее из чисел $\underline S$, ограничивающее сверху множество {$S$}, называется нижней П. фигуры $F$, а наибольшее из чисел $\overline S$, ограничивающее снизу множество {$S$}, называется верхней П. фигуры $F$. Если верхняя П. фигуры совпадает с её нижней П., то число $S=\overline S=\underline S$ называется площадью фигуры, а сама $F$ квадрируемой фигурой. Для того чтобы плоская фигура была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа $ε$ можно было указать такой описанный вокруг фигуры многоугольник и такой вписанный в фигуру многоугольник, разность $S-s$ площадей которых была бы меньше $ε$.
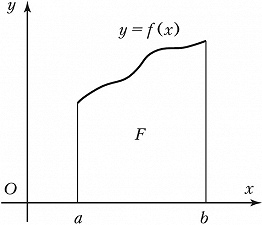
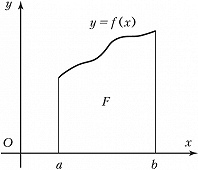
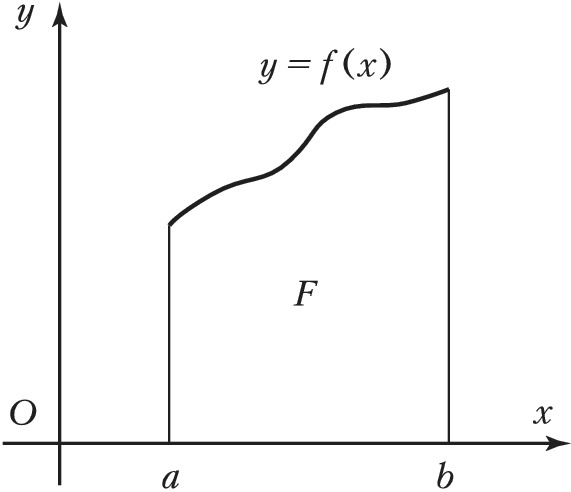
Аналитически П. плоской фигуры может быть вычислена с помощью интеграла. Пусть фигура $F$ – т. н. криволинейная трапеция (рис. 1) – ограничена графиком заданной на отрезке $[a, b]$ непрерывной неотрицательной функции $f(x)$, отрезками прямых $x=a$ и $x=b$ и отрезком $[a, b]$ оси $Ox$. П. такой фигуры может быть выражена интегралом $$S=\int\limits_a^b f(x)dx.$$ П. фигуры, ограниченной замкнутым контуром, который встречается с каждой прямой, параллельной к оси $Oy$, не более чем в двух точках, может быть вычислена как разность П. двух криволинейных трапеций. П. фигуры может быть выражена в виде двойного интеграла $$S=\iint\limits_F dxdy,$$ где интегрирование ведётся по части плоскости, занятой фигурой.
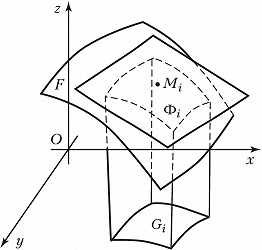
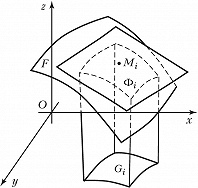
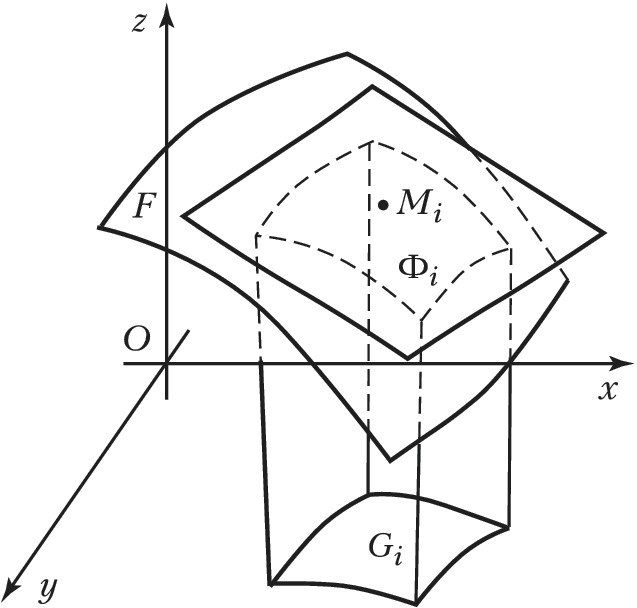
Теория П. фигур, расположенных на кривой поверхности, может быть построена следующим образом. Пусть $F$ – односвязная фигура на гладкой поверхности, ограниченная кусочно гладким контуром. Фигура $F$ разбивается кусочно гладкими кривыми на конечное число частей $Φ_i$, каждая из которых однозначно проектируется на касательную плоскость, проходящую через точку $M_i∈Φ_i$ (рис. 2). Предел сумм площадей этих проекций (если он существует), взятых по всем элементам разбиения, при условиях, что он существует и не зависит от выбора точек $M_i$, называется площадью фигуры $F$, а сама $F$ называется квадрируемой. Аналитически П. фигуры $F$ на поверхности, заданной уравнением $z=f(x, y)$, может быть выражена интегралом $$S=\iint\limits_G\sqrt{1+(f'_x)^2+(f'_y)^2dxdy},$$ где $G$ – замкнутая область, являющаяся проекцией $F$ на плоскость $Oxy$.
В Междунар. системе единиц (СИ) П. измеряется в м2.
Об обобщении понятия П. см. в ст. Мера множества.