ПАСКА́ЛЯ УЛИ́ТКА

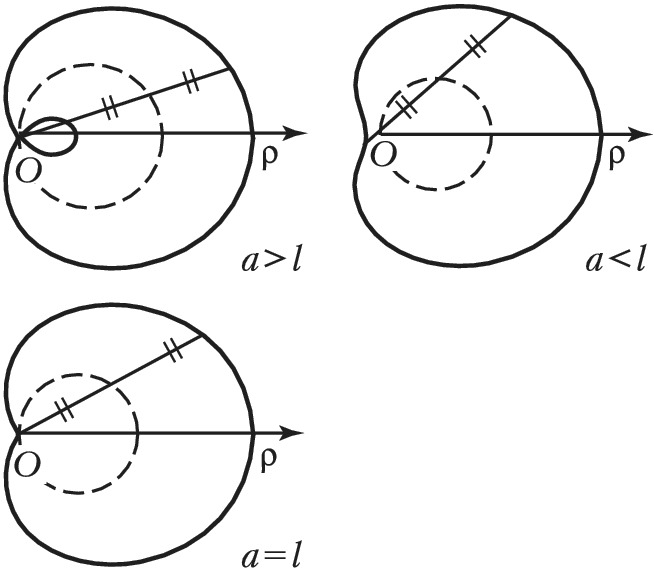
ПАСКА́ЛЯ УЛИ́ТКА, пло­ская ал­геб­раи­че­ская кри­вая 4-го по­ряд­ка. Урав­не­ние в пря­мо­уголь­ных ко­ор­ди­на­тах $$(x^2+y^2-ax)^2=l^2(x^2+y^2),$$ в по­ляр­ных ко­ор­ди­на­тах$$ρ=a \cos φ+l.$$ Сим­мет­рич­на от­но­си­тель­но оси $Ox$ (рис.). На­ча­ло ко­ор­ди­нат – двой­ная точ­ка, изо­ли­ро­ван­ная при $a \lt l$, уз­ло­вая при $a\gt l$, точ­ка воз­вра­та 1-го ро­да (см. Осо­бая точ­ка) при $a=l$ (в этом слу­чае П. у. – кар­дио­ида, см. Ли­ния). Дли­на ду­ги вы­ра­жа­ет­ся эл­лип­тич. ин­те­гра­лом 2-го ро­да. Пло­щадь, ог­ра­ни­чен­ная П. у., $S=πa^2/2+πl^2$; при $a \gt l$ пло­щадь внут­рен­ней пет­ли при вычис­ле­нии по этой фор­му­ле счи­та­ет­ся два­ж­ды. П. у. – ча­ст­ный слу­чай де­кар­то­ва ова­ла.

На­зва­на по име­ни франц. ма­те­ма­ти­ка-лю­би­те­ля Э. Пас­ка­ля, от­ца Б. Пас­ка­ля, впер­вые рас­смот­рев­ше­го её в 1-й пол. 17 в.