ДВОЙНО́Е ОТНОШЕ́НИЕ

ДВОЙНО́Е ОТНОШЕ́НИЕ че­ты­рёх то­чек $M_1$, $M_2$, $M_3$, $M_4$ на пря­мой, чис­ло, обо­зна­чае­мое сим­во­лом ($M_1M_2M_3M_4$) и рав­ное  $$\frac {M_1M_3}{M_3M_2}: \frac {M_1M_4}{M_4M_2},$$  где $M_iM_j$, $i$, $j=$1, 2, 3, 4, $i\neq j$, оз­на­ча­ет дли­ну от­рез­ка, со­еди­няю­ще­го точ­ки $M_i$и $M_j$. При этом учи­ты­ва­ют­ся на­прав­ле­ния от­рез­ков; напр., от­но­ше­ние$M_1M_3/M_3M_2$ счи­та­ет­ся по­ло­жи­тель­ным, ес­ли на­прав­ле­ния от­рез­ков $M_1M_3$ и $M_3M_2$ сов­па­да­ют, и от­ри­ца­тель­ным в про­тив­ном слу­чае. Д. о. за­ви­сит от по­ряд­ка ну­ме­ра­ции то­чек, ко­то­рый мо­жет от­ли­чать­ся от по­ряд­ка сле­до­ва­ния то­чек на пря­мой.

          На­ря­ду с Д. о. че­ты­рёх то­чек рас­смат­ри­ва­ет­ся Д. о. че­ты­рёх пря­мых $m_1, m_2, m_3, m_4$, про­хо­дя­щих че­рез об­щую точ­ку $O$. Это от­но­ше­ние обо­зна­ча­ет­ся сим­во­лом ($m_1m_2m_3m_4$) и рав­но  $$\frac {\sin(m_1m_3)}{\sin(m_3m_2)}:\frac {\sin(m_1m_4)}{\sin(m_4m_2)},$$ при­чём уг­лы ($m_im_j$) ме­ж­ду пря­мы­ми $m_i$ и $m_j$, $i$, $j=$1, 2, 3, 4, $i \neq j$, рас­смат­ри­ва­ют­ся со зна­ка­ми.

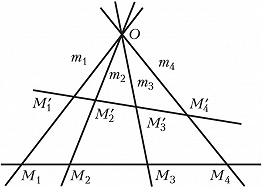
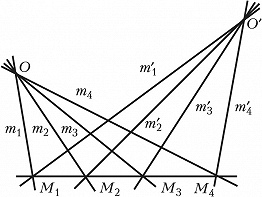
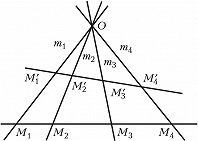
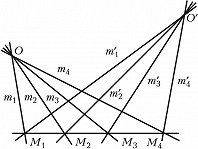
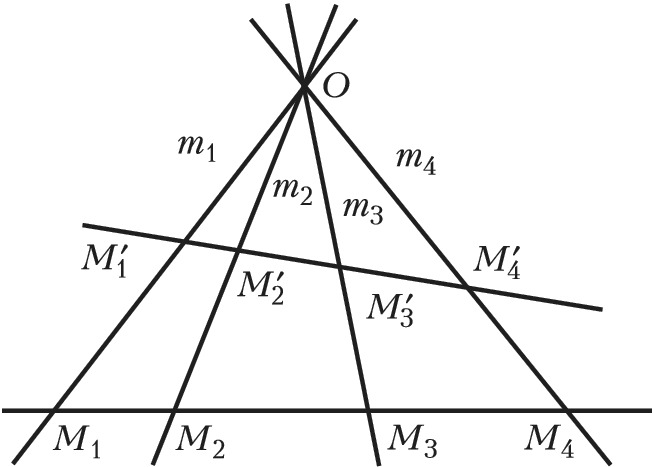
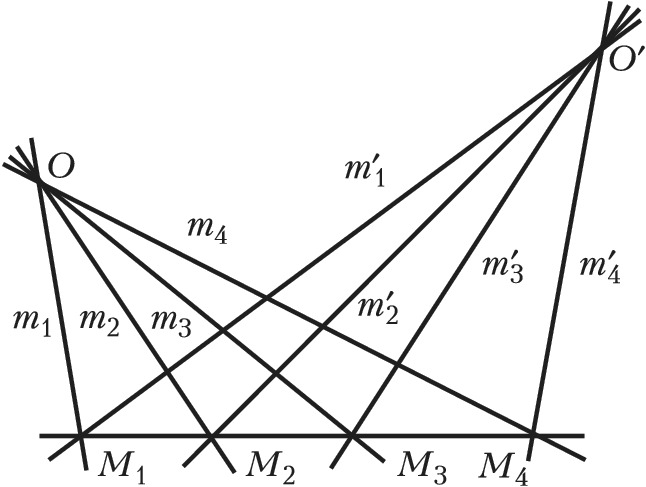
Ес­ли точ­ки $M_1$, $M_2$, $M_3$, $M_4$ ле­жат на пря­мых $m_1$, $m_2$, $m_3$, $m_4$ (рис. 1), то $(M_1M_2M_3M_4)$=$(m_1m_2m_3m_4)$. Ес­ли точки $M_1$, $M_2$, $M_3$, $M_4$ и $M'_1$, $M'_2$, $M'_3$, $M'_4$ по­лу­че­ны пе­ре­се­че­ни­ем од­ной чет­вёр­ки пря­мых $m_1$, $m_2$, $m_3$, $m_4$ дву­мя разл. прямы­ми, то $(M'_1M'_2M'_3M'_4)$= $(M_1M_2M_3M_4)$. Ес­ли же пря­мые $m_1$, $m_2$, $m_3$, $m_4$ и $m'_1$, $m'_2$, $m'_3$, $m'_4$ про­ек­ти­ру­ют од­ну чет­вёр­ку то­чек $M_1$, $M_2$, $M_3$, $M_4$ (рис. 2), то $(m'_1m'_2m'_3m'_4)$= $(m_1m_2m_3m_4)$. Д. о. не ме­ня­ет­ся при лю­бом про­ек­тив­ном пре­об­ра­зо­ва­нии

, т. е. яв­ля­ет­ся ин­ва­ри­ан­том это­го пре­об­ра­зо­ва­ния, по­это­му Д. о. важ­ны в про­ек­тив­ной гео­мет­рии

 >>

. Осо­бую роль иг­ра­ют чет­вёр­ки то­чек и пря­мых, для ко­то­рых Д. о. рав­но –1. Та­кие чет­вёр­ки на­зы­ва­ют­ся гар­мо­ни­че­ски­ми.