ПОВЕ́РХНОСТНАЯ ЭНЕ́РГИЯ

Рис. 1. Межмолекулярные взаимодействия в объёме жидкости и на поверхности.

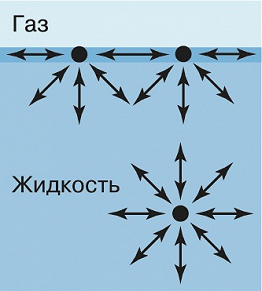
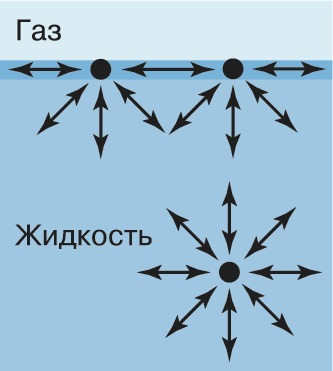
ПОВЕ́РХНОСТНАЯ ЭНЕ́РГИЯ, энер­гия мо­ле­кул, ато­мов, ио­нов, на­хо­дя­щих­ся в тон­ком пе­ре­ход­ном слое, рас­по­ло­жен­ном в не­по­сред­ст­вен­ной бли­зо­сти от гра­ни­цы раз­де­ла двух и бо­лее фаз, имею­щая бо­лее вы­со­кое по­ло­жи­тель­ное зна­че­ние по срав­не­нию с энер­ги­ей мо­ле­кул, ато­мов, ио­нов, на­хо­дя­щих­ся в ана­ло­гич­ном объ­ё­ме, рас­по­ло­жен­ном внут­ри фа­зы. По­вы­шен­ный уро­вень энер­гии на по­верх­но­сти фа­зы яв­ля­ет­ся след­ст­ви­ем из­бы­точ­ной по­тен­ци­аль­ной (сво­бод­ной) энер­гии мо­ле­кул, ато­мов или ио­нов, на­хо­дя­щих­ся в по­ле дей­ст­вия не­сим­мет­рич­ных сил при­тя­же­ния и реа­ли­зую­щих лишь часть воз­мож­ных взаи­мо­дей­ст­вий (об­ра­зо­ва­ния ко­ва­лент­ных, ион­ных, до­нор­но-ак­цеп­тор­ных, ван-дер-ва­аль­со­вых и пр. свя­зей), а так­же на­ли­чия из­бы­точной ки­не­ти­че­ской (те­п­ло­вой) энер­гии, вы­зван­ной боль­шей под­виж­но­стью (бóльшим ко­ли­че­ст­вом сте­пе­ней сво­бо­ды) мо­ле­кул, ато­мов, ио­нов, рас­по­ло­жен­ных в по­верх­но­ст­ном слое. Рав­но­дей­ст­вую­щая сил, ока­зы­ваю­щих влия­ние на мо­ле­ку­лу в по­верх­но­ст­ном слое, на­прав­ле­на внутрь жид­ко­сти, то­гда как взаи­мо­дей­ст­вие мо­ле­ку­лы с со­сед­ни­ми в объ­ё­ме при­мер­но рав­но­цен­но (рис. 1).

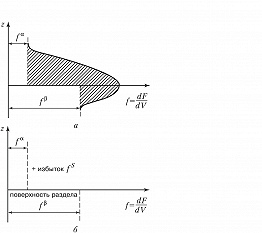
П. э. рав­но­вес­ной сис­те­мы мо­жет быть вы­ра­же­на с ис­поль­зо­ва­ни­ем всех из­вест­ных тер­мо­ди­на­мич. функ­ций. Как и др. ви­ды энер­гии, П. э. яв­ля­ет­ся экс­тен­сив­ной ве­ли­чи­ной и про­пор­цио­наль­на пло­ща­ди гра­ни­цы раз­де­ла фаз. Ко­ли­че­ст­вен­но П. э. оп­ре­де­ля­ет­ся ин­те­граль­ным вы­ра­же­ни­ем, учи­ты­ваю­щим собств. энер­гию всех ато­мов, мо­ле­кул, ио­нов, при­над­ле­жа­щих пе­ре­ход­но­му слою. В ча­ст­но­сти, ин­те­граль­ная ве­ли­чи­на изо­хор­но-изо­тер­мич. по­тен­циа­ла (сво­бод­ной энер­гии, см. Гельм­голь­ца энер­гия) $F$, вы­ра­жен­ная че­рез плот­ность сво­бод­ной энер­гии $\left( \frac{dF}{dV} \right)_{V\rightarrow 0}=f$, мо­жет быть пред­став­ле­на как $F=s \cdot\left( \int^0_{-\delta'}\left( \frac{dF}{dV}\right)dz+\int_0^{+\delta''}\left( \frac{dF}{dV}\right)dz \right)$ ($s$ – пло­щадь по­верх­но­сти раз­де­ла фаз, $V$ – объ­ём). Ис­поль­зо­ва­ние это­го вы­ра­же­ния тре­бу­ет зна­ния не толь­ко тол­щин пе­ре­ход­ных сло­ёв со сто­ро­ны ка­ж­дой из кон­так­ти­рую­щих фаз ($δ′$ и $δ″$), но и ин­фор­ма­ции о ха­рак­те­ре за­ви­си­мо­сти энер­гии от рас­стоя­ния ($z$) в по­верх­но­ст­ном слое, ко­то­рую пре­дос­тав­ля­ет ме­тод сло­ёв ко­неч­ной тол­щи­ны.

Рис. 2. Изменение плотности свободной энергии на межфазной границе в реальной системе (а) и в модели Гиббса (б).

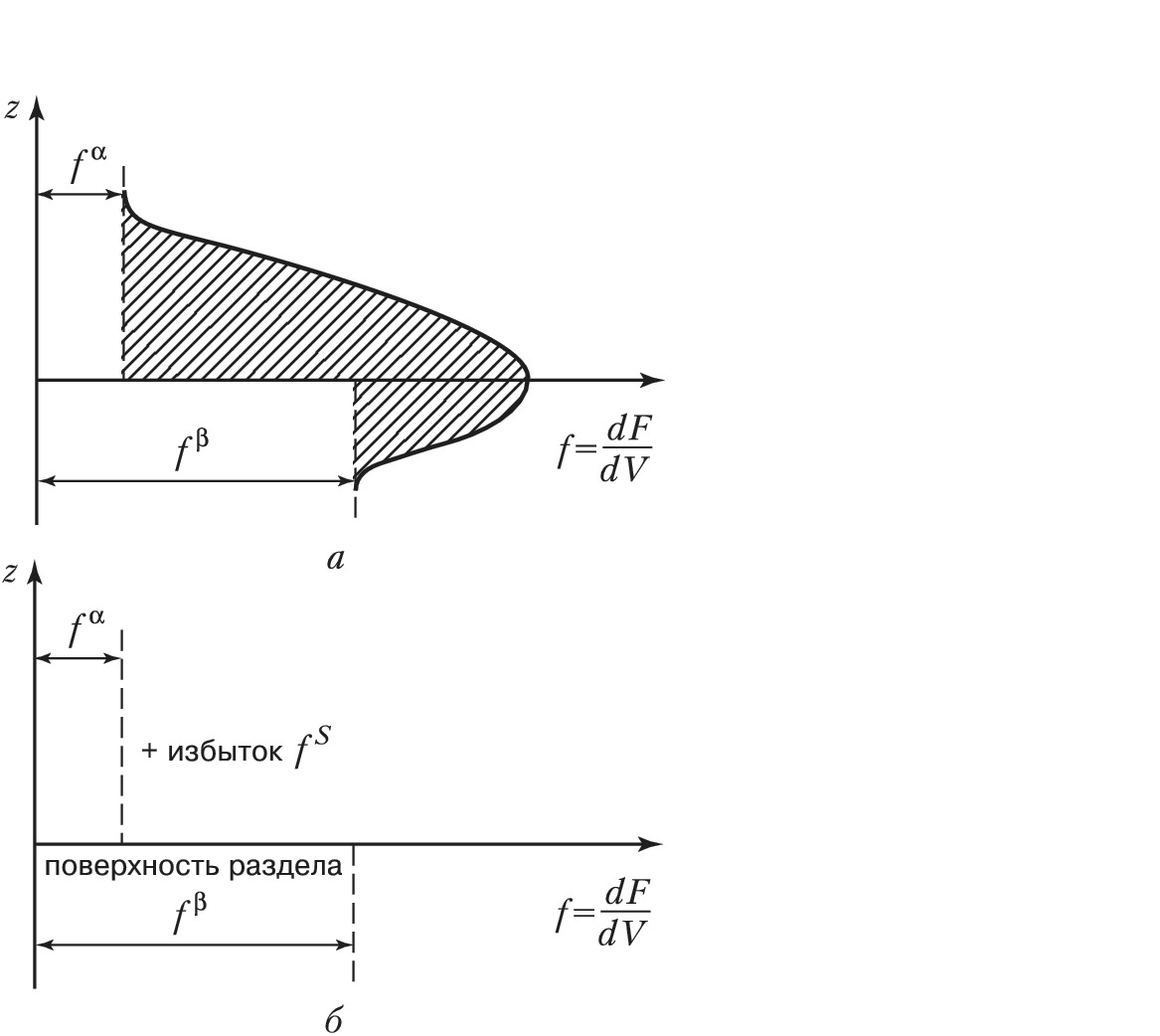
Бо­лее про­стым спо­со­бом опи­са­ния тер­мо­ди­на­мич. свойств по­верх­но­сти яв­ля­ет­ся ме­тод из­бы­точ­ных ве­ли­чин Гиб­бса, со­глас­но ко­то­ро­му име­ет­ся идеа­ли­зи­ро­ван­ная сис­те­ма, со­стоя­щая из двух фаз ($α$ и $β$) с раз­де­ляю­щей по­верх­но­стью, ко­то­рой свой­ст­вен­ны из­быт­ки тер­мо­ди­на­мич. ха­рак­те­ри­стик – энер­гии, эн­тро­пии и со­дер­жа­ния ком­по­нен­тов (рис. 2). В этом слу­чае в тер­мо­ди­на­мич. урав­нени­ях фи­гу­ри­ру­ют не аб­со­лют­ные, а из­бы­точ­ные экс­тен­сив­ные ве­ли­чи­ны. Напр., из­бы­ток чис­ла мо­лей ком­по­нентов на по­верх­но­сти вы­ра­жа­ет­ся урав­нени­ем: $\Delta n_i=n_i-n_i^{\alpha}\cdot V_i^{\alpha}-n_i^{\beta}\cdot V_i^{\beta}=n_i^s$ ($n_i$ – чис­ло мо­лей $i$-го ком­по­нен­та). Выра­жение для из­бы­точ­ной П. э. оп­реде­ля­ет­ся как $F^s=F-F^{\alpha}-F^{\beta}=s\cdot \left( \int^0_{-\delta'}(f(z)-f^{\alpha})dz+\int_0^{+\delta''}(f(z)-f^{\beta})dz\right)$. Как вид­но из ри­сун­ка, при та­ком под­хо­де ве­ли­чи­на П. э. ока­зы­ва­ет­ся за­ви­ся­щей от по­ло­же­ния раз­де­ляю­щей по­верх­но­сти.

На­ли­чие не­ском­пен­си­ро­ван­ных сил при­тя­же­ния на гра­ни­це раз­де­ла при­во­дит к по­яв­ле­нию (на­ря­ду с из­бы­точ­ной П. э.) си­лы, на­прав­лен­ной тан­ген­ци­аль­но, вдоль ог­ра­ни­чи­ваю­ще­го по­верх­ность кон­ту­ра. Эта си­ла, на­зы­вае­мая по­верх­но­ст­ным на­тя­же­ни­ем σ, пре­пят­ст­ву­ет уве­ли­че­нию меж­фаз­ной по­верх­но­сти. К по­верх­но­стям, раз­де­ляю­щим кон­ден­си­ро­ван­ные фа­зы, обыч­но при­ме­ня­ет­ся тер­мин «меж­фаз­ное на­тя­же­ние».

Ес­ли, ис­поль­зуя ме­тод Гиб­бса, при­ме­ни­тель­но к по­верх­но­ст­но­му слою за­пи­сать урав­не­ния 1-го и 2-го за­ко­нов тер­мо­ди­на­ми­ки для от­кры­той двух­фаз­ной сис­те­мы с учё­том дей­ст­вия сил по­верх­но­ст­но­го на­тя­же­ния, то мо­жет быть по­лу­че­но фун­дам. урав­не­ние Гиб­бса: $dF^s=\sigma\cdot ds-S^s\cdot dT+\sum μ_i\cdot dn_i^s$ ($S$ – эн­тро­пия, $T$ – темп-ра, $μ_i$ – хи­мич. по­тен­ци­ал $i$-го ком­по­нен­та). Из не­го сле­ду­ет, что по­верх­но­ст­ное на­тя­же­ние яв­ля­ет­ся ча­ст­ной про­из­вод­ной сво­бод­ной энер­гии (а так­же лю­бо­го др. тер­мо­ди­на­мич. по­тен­циа­ла) по по­верх­но­сти при по­сто­ян­ст­ве со­от­вет­ст­вую­щих пе­ре­мен­ных: $\left( \frac{\partial F^s}{\partial s}\right)_{T,V,\sum n_i}=\delta$. Для од­но­ком­по­нент­ной фа­зы оно чис­лен­но сов­па­да­ет с ве­ли­чиной удель­ной сво­бод­ной из­бы­точ­ной П. э., рав­ной и про­ти­во­по­лож­ной по зна­ку ра­бо­те об­ра­зо­ва­ния еди­ни­цы но­вой по­верх­но­сти.

Рас­счи­тать пол­ную внут­рен­нюю энер­гию по­верх­но­сти $U_s$ по ме­то­ду Гиб­бса мож­но, экс­пе­ри­мен­таль­но оп­ре­де­лив ве­ли­чи­ну по­верх­но­ст­но­го на­тя­же­ния и его тем­пе­ра­тур­ный ко­эф., ко­то­рый все­гда от­ри­ца­те­лен (что оз­на­ча­ет су­ще­ст­во­ва­ние из­быт­ка эн­тро­пии в по­верх­но­ст­ном слое): $U_s=\sigma-T \cdot \frac{\partial \sigma}{\partial T}$. Важ­но, что, в от­ли­чие от П. э. в ме­то­де из­бы­точ­ных ве­ли­чин, по­верх­но­ст­ное на­тя­же­ние в слу­чае пло­ской гра­ни­цы раз­де­ла не за­ви­сит от вы­бо­ра по­ло­же­ния по­верх­но­сти. Оно яв­ля­ет­ся ха­рак­те­ри­сти­кой сил, дей­ст­вую­щих в по­верх­но­ст­ном слое, и опи­сы­ва­ет­ся ин­те­гра­лом тан­ген­ци­аль­ной ком­по­нен­ты тен­зо­ра дав­ле­ния, ко­то­рая от­ли­ча­ет­ся от гид­ро­ста­тич. нор­маль­но­го дав­ле­ния и яв­ля­ет­ся от­ри­ца­тель­ной ве­ли­чи­ной: $\sigma=\int_{-\delta'}^{+\delta''}[p-p(z)]dz$.

Ес­ли по­верх­ность раз­де­ла ока­зы­ва­ет­ся ис­крив­лён­ной, дей­ст­вие сил по­верх­но­ст­но­го на­тя­же­ния в по­верх­но­ст­ном слое при­во­дит к по­яв­ле­нию раз­ни­цы нор­маль­ных дав­ле­ний в фа­зах, ко­то­рая за­ви­сит от ин­тен­сив­но­сти дей­ст­вия сил по­верх­но­ст­но­го на­тя­же­ния и от ос­нов­ных ра­диу­сов кри­виз­ны по­верх­но­сти $r_1$ и $r_2$: $\Delta p=\sigma \left( \frac{1}{r_1}+\frac{1}{r_2}\right)$ или $\Delta p=\frac{2\sigma}{r}$ для сфе­рич. по­верх­но­сти ка­п­ли. Это урав­не­ние, из­вест­ное как урав­не­ние Ла­п­ласа, пред­ска­зы­ва­ет на­ли­чие боль­шо­го внут­рен­не­го дав­ле­ния в мик­ро­раз­мер­ных и осо­бен­но на­но­раз­мер­ных час­ти­цах. Удель­ная по­верх­ность (т. е. от­но­ше­ние сум­мар­ной по­верх­но­сти к объ­ё­му) та­ких час­тиц ог­ром­на, а зна­чит, не­обы­чай­но ве­лик за­пас П. э. По­это­му лю­бая мик­ро- или на­но­дис­пер­сия да­ле­ко не рав­но­вес­на и пе­ре­хо­дит в бо­лее ус­той­чи­вое со­стоя­ние, напр., пу­тём коа­гу­ля­ции, пе­ре­кон­ден­са­ции или ад­сорб­ции.

На мик­ро- и на­но­уров­не по­верх­но­сти твёр­дых тел обыч­но ше­ро­хо­ва­ты и энер­ге­ти­че­ски неод­но­род­ны. Тем не ме­нее их то­же ха­рак­те­ри­зу­ют ве­ли­чи­ной П. э., оп­ре­де­ле­ние ко­то­рой воз­мож­но, напр., пу­тём экс­т­ра­по­ля­ции тем­пе­ра­тур­ной за­ви­си­мо­сти по­верх­но­ст­но­го на­тя­же­ния рас­пла­ва, из дан­ных сма­чи­ва­ния (для аморф­ных тел), ме­то­дом «за­ле­чи­ваю­щей­ся ца­ра­пи­ны» или из ра­бо­ты рас­ка­лы­ва­ния кри­стал­ла.

П. э. иг­ра­ет ог­ром­ную роль в сма­чи­ва­нии, рас­те­ка­нии, ад­сорб­ции, ка­пил­ляр­ных эф­фек­тах, по­лу­че­нии и ус­той­чи­во­сти дис­перс­ных сис­тем, а так­же оп­ре­де­ля­ет под­хо­ды к реа­ли­за­ции мн. тех­но­ло­гич. про­цес­сов.