КРУЧЕ́НИЕ

Рис. 1. Кручение круглого прямого стержня.

КРУЧЕ́НИЕ в со­про­тив­ле­нии ма­те­риа­лов, вид де­фор­ма­ции, ха­рак­те­ри­зую­щий­ся вза­им­ным по­во­ро­том по­пе­реч­ных се­че­ний де­фор­ми­руе­мо­го те­ла под влия­ни­ем мо­мен­тов (пар сил), дей­ст­вую­щих в этих се­че­ни­ях; при этом в по­пе­реч­ных се­че­ни­ях де­фор­ми­руе­мо­го те­ла воз­ни­ка­ет кру­тя­щий мо­мент. По­пе­реч­ные се­че­ния круг­лых стерж­ней (ва­лов) при К. ос­та­ют­ся пло­ски­ми; при К. приз­ма­тич. стерж­ней про­ис­хо­дит де­пла­на­ция се­че­ния (ис­крив­ле­ние се­че­ния за счёт не­рав­но­мер­но­сти пе­ре­ме­ще­ния его то­чек). Ес­ли де­пла­на­ция во всех се­че­ни­ях по дли­не стерж­ня оди­на­ко­ва, то К. на­зы­ва­ет­ся сво­бод­ным (чис­тым); при сво­бод­ном К. в по­пе­реч­ных се­че­ни­ях воз­ни­ка­ют толь­ко ка­са­тель­ные на­пря­же­ния. При пе­ре­мен­ных по дли­не стерж­ня де­пла­на­ци­ях се­че­ний (при на­ли­чии за­дел­ки, из­ме­не­нии кру­тя­щих на­гру­зок по дли­не стерж­ня и др.) К. на­зы­ва­ет­ся стес­нён­ным (из­гиб­ным); оно ха­рак­те­ри­зу­ет­ся тем, что на­ря­ду с ка­са­тель­ны­ми в по­пе­реч­ных се­че­ни­ях стерж­ня воз­ни­ка­ют так­же нор­маль­ные на­пря­же­ния.

Рис. 2. Распределение касательных напряжений в упругой (а), упругопластической (б) и пластической (в) стадиях работы материала стержня.

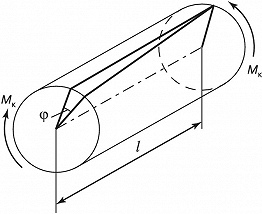
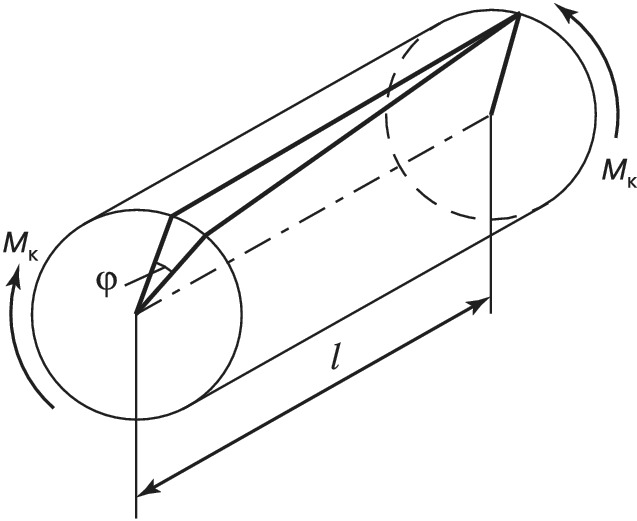
Наи­бо­лее час­то встре­чаю­щим­ся в прак­ти­ке слу­ча­ем яв­ля­ет­ся К. круг­ло­го пря­мо­го стерж­ня (рис. 1). В ре­зуль­та­те дей­ст­вия кру­тя­ще­го мо­мен­та $M_к$ в по­пе­реч­ных се­чени­ях стерж­ня воз­ни­ка­ют ка­са­тель­ные на­пря­же­ния $τ$ , а се­че­ния стерж­ня (рас­стоя­ние ме­ж­ду ко­то­ры­ми рав­но $l$) по­во­ра­чи­ва­ют­ся од­но от­но­си­тель­но дру­го­го на угол за­кру­чи­ва­ния $φ$. Угол за­кру­чи­ва­ния на еди­ни­цу дли­ны стерж­ня на­зы­ва­ют от­но­си­тель­ным уг­лом за­кру­чи­ва­ния $\theta $. При сво­бод­ном К. в уп­ру­гой ста­дии от­но­си­тель­ный угол за­кру­чи­ва­ния и наи­боль­шие ка­са­тель­ные на­пря­же­ния $τ_{макс}$ оп­ре­де­ля­ют­ся по фор­му­лам: $$\theta=\frac {M_к}{GI_к},\tau_{макс}=\frac{M_к}{W_к},$$где $G$ – мо­дуль уп­ру­го­сти при сдви­ге, $I_к$ и $W_к$ – со­от­вет­ст­вен­но ус­лов­ный мо­мент инер­ции и мо­мент со­про­тив­ле­ния при К. В круг­лых се­че­ни­ях $I_к$ пред­став­ля­ет со­бой по­ляр­ный мо­мент инер­ции $I_p=πr^4/2$, а Wк – по­ляр­ный мо­мент со­про­тив­ле­ния Wp=πr3/2. Про­из­ве­де­ние $GI_p$ на­зы­ва­ет­ся жё­ст­ко­стью круг­ло­го се­че­ния при К. Для пря­мо­уголь­ных се­че­ний с боль­шей сто­ро­ной $h$ и мень­шей $b$: $I_к=αhb^3, W_к=βhb^2$, где ко­эф­фи­ци­ен­ты $α$ и $β$ оп­ре­де­ля­ют­ся в за­ви­си­мо­сти от от­но­ше­ния $h/b$ по таб­ли­цам.

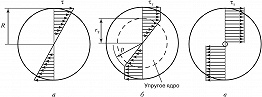
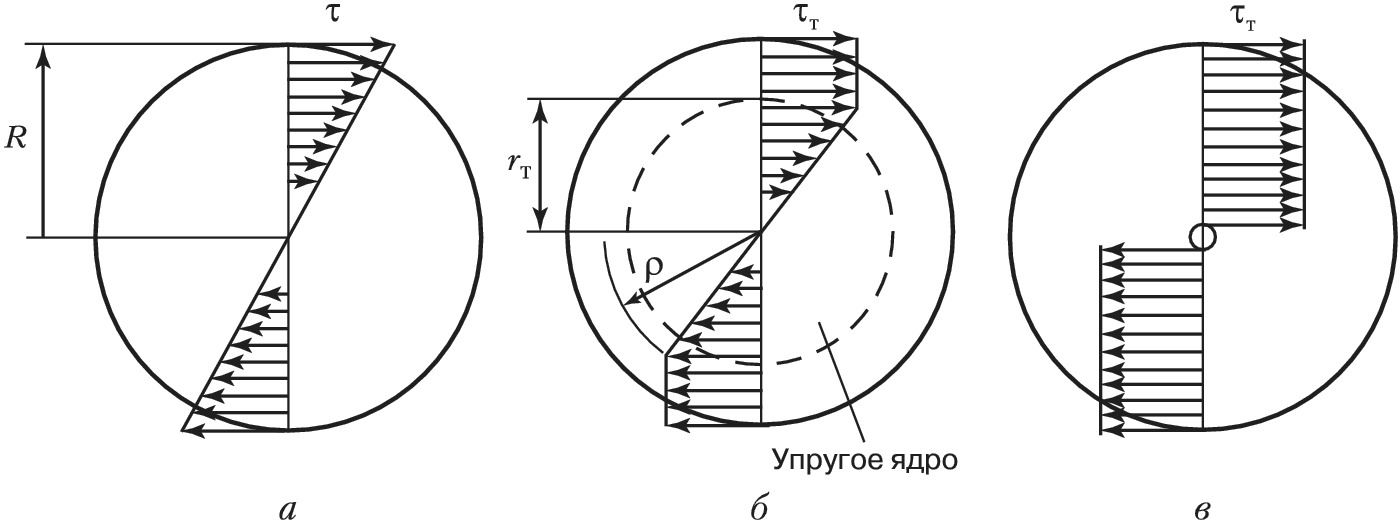
При К. круг­ло­го ва­ла с ра­диу­сом R в уп­ру­гой ста­дии ка­са­тель­ные на­пря­жения $(\tau=\frac{M_к}{I_p}\rho)$ рас­пре­де­ля­ют­ся в по­переч­ном се­че­нии по ли­ней­но­му за­ко­ну (рис. 2,а), где $ρ$ – рас­стоя­ние от оси вала до рас­смат­ри­вае­мой точ­ки се­че­ния. В уп­ру­го­пла­стич. ста­дии (рис. 2,б) ка­са­тель­ные на­пря­же­ния, со­от­вет­ст­вую­щие пре­де­лу те­ку­че­сти $(τ_т)$, рас­про­стра­ня­ют­ся от по­верх­но­сти к оси ва­ла, а всё се­че­ние раз­де­ля­ет­ся на две зо­ны: уп­ру­гое яд­ро с ра­диу­сом $r_т$, в ко­то­ром $τ⩽τ_т$, и пла­стич. коль­це­вую зо­ну $r_т⩽ρ⩽R$, в ко­то­рой $τ=τ_т$. В пре­дель­ном со­стоя­нии (рис. 2,в) пла­стич. зо­на ох­ва­ты­ва­ет всё се­че­ние (та­кое со­стоя­ние стерж­ня на­зы­ва­ет­ся пла­стич. шар­ни­ром), при этом пре­дель­ный кру­тя­щий мо­мент для круг­ло­го се­че­ния: $$M_{пред}=\frac{2}{3}(\tau_Т\pi r^2).$$

При К. пла­стин и обо­ло­чек про­ис­хо­дит ис­крив­ле­ние сре­дин­ной по­верх­но­сти вслед­ст­вие пе­ре­ме­ще­ния её то­чек в на­прав­ле­нии нор­ма­лей; в ра­бо­те кон­ст­рук­ций этих ти­пов К. со­пут­ст­ву­ют де­фор­ма­ции из­ги­ба.