ВЗАИ́МНОСТИ ТЕО́РИЯ

ВЗАИ́МНОСТИ ТЕО́РИЯ. В ос­но­ве В. т. ле­жат че­ты­ре осн. прин­ци­па (тео­ре­мы) вза­им­но­сти.

Прин­цип вза­им­но­сти ра­бот (тео­ре­ма Бет­ти): при рас­смот­ре­нии двух со­стоя­ний $(i\: и\: k)$ уп­ру­го­го те­ла, ка­ж­дое из ко­то­рых оп­ре­де­ля­ет­ся дей­ст­ви­ем обоб­щён­ной си­лы со­от­вет­ст­вен­но $P_i$ или $P_k$, ра­бо­та внеш­них или внут­рен­них сил со­стоя­ния $i$ на вы­зван­ных де­фор­ма­ци­ей пе­ре­ме­ще­ни­ях со­стоя­ния $k(W_{ik})$ рав­на ра­бо­те сил со­стоя­ния $k$ на пе­ре­ме­ще­ни­ях со­стоя­ния $i(W_{ki})$, т. е. $W_{ik}=W_{ki}$.

Прин­цип вза­им­но­сти ра­бот до­ка­зан итал. учё­ным Э. Бет­ти (1872). След­ст­ви­ем прин­ци­па вза­им­но­сти ра­бот яв­ля­ют­ся тео­ре­мы вза­им­но­сти пе­ре­ме­ще­ний, взаимности ре­ак­ций и тео­ре­ма вза­им­но­сти ре­ак­ций и пе­ре­ме­ще­ний.

Рис. 1.

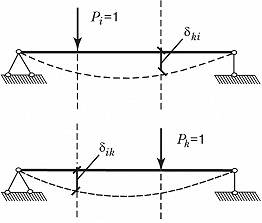
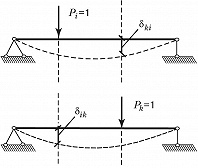
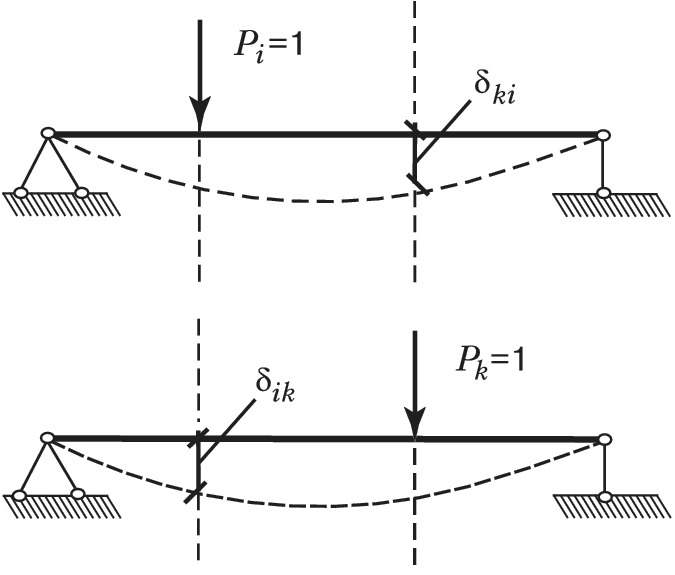
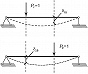
Тео­ре­ма вза­им­но­сти пе­ре­ме­ще­ний (тео­ре­ма Мак­свел­ла): при рас­смот­ре­нии двух со­стоя­ний те­ла $(i \:и\: k)$, ка­ж­дое из ко­то­рых оп­ре­де­ля­ет­ся дей­ст­ви­ем еди­нич­ной обоб­щён­ной си­лы со­от­вет­ст­вен­но $P_i$ или $P_k$, пе­ре­ме­ще­ние со­стоя­ния $i$ по на­прав­ле­нию дей­ст­вия си­лы $P_k(δ_{ki})$ рав­но пе­ре­ме­ще­нию со­стоя­ния $k$ по на­прав­ле­нию си­лы $P_i(δ_{ik})$, т. е. $δ_{ki}=δ_{ik}$ (рис. 1). Тео­ре­ма опуб­ли­ко­ва­на Дж. К. Мак­свел­лом в 1864.

Рис. 2.

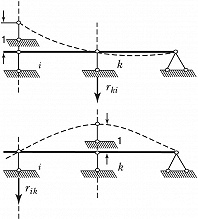
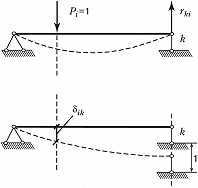
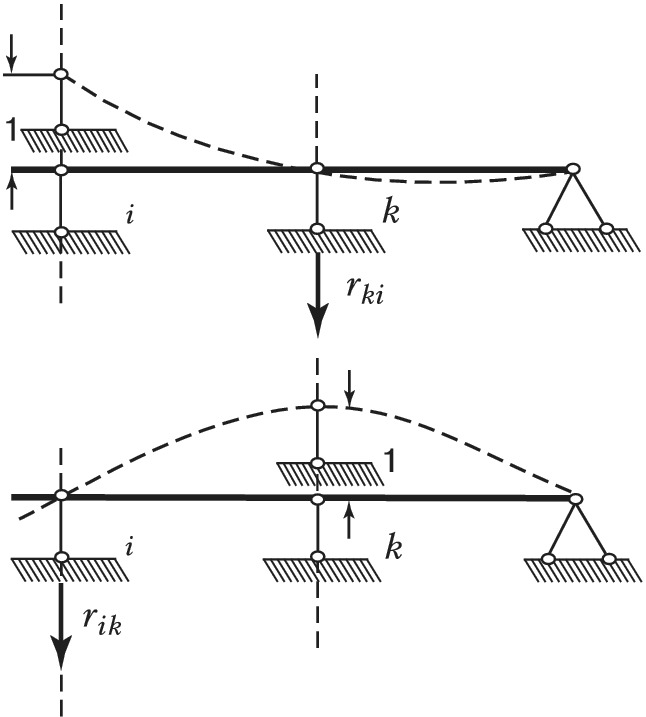
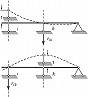
Тео­ре­ма вза­им­но­сти ре­ак­ций (тео­ре­ма Рэ­лея): при рас­смот­ре­нии двух со­стоя­ний те­ла $(i \:и\: k)$, ка­ж­дое из ко­то­рых оп­ре­де­ля­ет­ся еди­нич­ным сме­ще­ни­ем свя­зи со­от­вет­ст­вен­но $i$ или $k$, ре­ак­ция в свя­зи $k\: i$-го со­стоя­ния $(r_{ki})$ рав­на ре­ак­ции в свя­зи $i \:k$-го со­стоя­ния $(r_{ik})$, т. е. $r_{ki}=r_{ik}$ (рис. 2). Тео­ре­ма о вза­им­но­сти ре­ак­ций бы­ла опуб­ли­ко­ва­на Дж. У. Рэ­ле­ем в 1873.

Рис. 3.

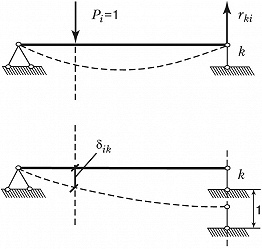
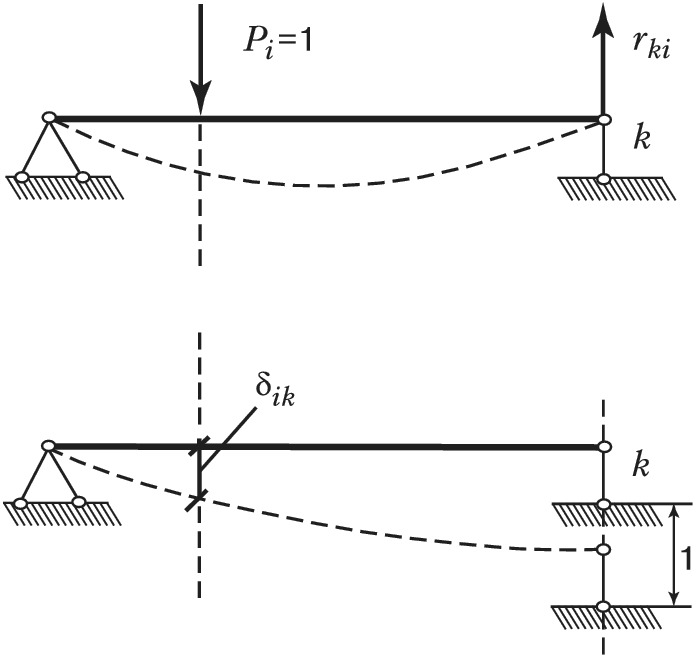
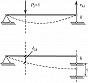
Тео­ре­ма вза­им­но­сти ре­ак­ций и пе­ре­ме­ще­ний: при рас­смот­ре­нии двух со­стоя­ний те­ла $(i \:и\: k)$, ка­ж­дое из ко­то­рых оп­ре­де­ля­ет­ся со­от­вет­ст­вен­но дей­ст­ви­ем еди­нич­ной обоб­щён­ной си­лы $P_i$ и еди­нич­ным сме­ще­ни­ем свя­зи $k$, ре­ак­ция в свя­зи $k\:i$-го со­стоя­ния $(r_{ki})$ рав­на по ве­ли­чи­не и об­рат­на по зна­ку пе­ре­ме­ще­нию со­стоя­ния $k$ по на­прав­ле­нию си­лы $P_i (δ_{ik})$, т. е. $r_{ki}=–δ_{ik}$ (рис. 3). Тео­ре­ма до­ка­за­на Дж. К. Мак­свел­лом в 1864 и Дж. У. Рэ­ле­ем в 1873.

Впер­вые прин­цип вза­им­но­сти для од­но­род­ной квад­ра­тич­ной фор­мы был сфор­му­ли­ро­ван О. Ко­ши в 1857. Ес­ли рас­смат­ри­вать квад­ра­тич­ную фор­му как вы­ра­же­ние по­тен­ци­аль­ной энер­гии, то от­сю­да сле­ду­ет один из важ­ней­ших прин­ци­пов ме­ха­ни­ки уп­ру­гих тел – прин­цип вза­им­но­сти ра­бот. Од­на­ко Ко­ши та­ко­го вы­во­да не сде­лал.

В. т. ши­ро­ко при­ме­ня­ют в стро­ит. ме­ха­ни­ке при рас­чё­тах уп­ру­гих сис­тем.