УДА́Р

УДА́Р твёр­дых тел, со­во­куп­ность яв­ле­ний, со­про­во­ж­даю­щих столк­но­ве­ние дви­жу­ще­го­ся те­ла с др. те­лом. Про­ме­жу­ток вре­ме­ни, в те­че­ние ко­то­ро­го про­те­ка­ет У., очень мал, но си­лы, воз­ни­каю­щие на пло­щад­ках кон­так­та, очень ве­ли­ки. Это при­во­дит к зна­чит. из­ме­не­нию ско­ро­стей то­чек те­ла, на­гре­ву те­ла и де­фор­ма­ции его по­верх­но­сти, воз­ник­но­ве­нию зву­ко­вых ко­ле­ба­ний и да­же раз­ру­ше­нию те­ла.

Прямой удар твёрдых тел: а – скорости тел до соударения, б – после соударения.

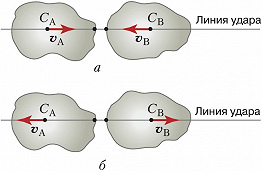
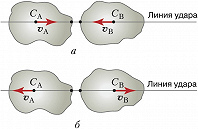
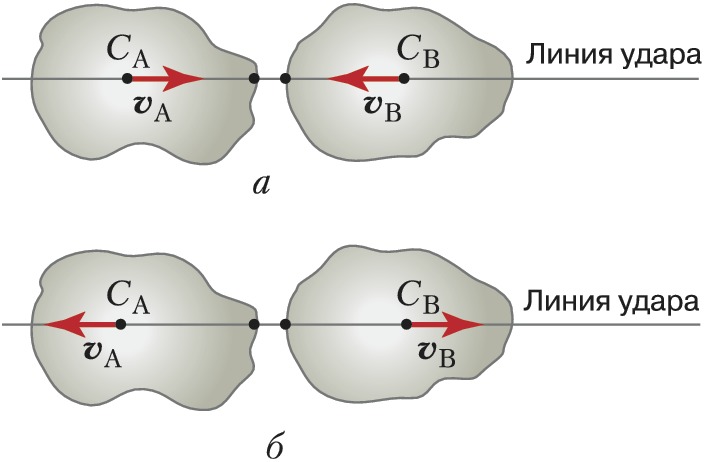
При рас­смот­ре­нии со­уда­ре­ния двух тел (рис.) вы­де­ля­ют пря­мой (цен­траль­ный) У., при ко­то­ром цен­тры масс тел С_А и С_В и век­то­ры ско­ро­стей цен­тров масс v_А и v_В ле­жат на т. н. ли­нии уда­ра (об­щей нор­ма­ли к по­верх­но­сти тел в точ­ке со­при­кос­но­ве­ния), и не­цен­траль­ный У. (в про­тив­ном слу­чае). При рас­смот­ре­нии У. ма­те­ри­аль­ной точ­ки о плос­кость пря­мым У. на­зы­ва­ют та­кой, при ко­то­ром век­тор ско­ро­сти пер­пен­ди­ку­ля­рен плос­ко­сти, в про­тив­ном слу­чае го­во­рят о ко­сом уда­ре.

Цен­траль­ный У. двух тел (напр., столк­но­ве­ние двух ша­ров) мож­но раз­де­лить на 2 фа­зы. Пер­вая фа­за на­чи­на­ет­ся с мо­мен­та кон­так­та и со­про­во­ж­да­ет­ся сбли­же­ни­ем тел. К кон­цу этой фа­зы сбли­же­ние за­вер­ша­ет­ся, часть ки­не­тич. энер­гии тел пе­ре­хо­дит в по­тен­ци­аль­ную энер­гию уп­ру­гих де­фор­ма­ций, часть тра­тит­ся на на­гре­ва­ние. Во 2-й фа­зе энер­гия де­фор­ма­ций пе­ре­хо­дит в ки­не­тич. энер­гию раз­ле­таю­щих­ся тел. Од­ной из ха­рак­те­ри­стик та­ко­го У. слу­жит ко­эф. вос­ста­нов­ле­ния 𝑘 – от­но­ше­ние ско­ро­сти v₂ рас­хо­ж­де­ния тел по­сле У. к на­чаль­ной ско­ро­сти v₁ сбли­же­ния. По экс­пе­рим. дан­ным, для тел из де­ре­ва 𝑘≈0,5, из ста­ли 𝑘≈0,55, из сло­но­вой кос­ти 𝑘≈0,89. В мо­дель­ных за­да­чах 𝑘=1 со­от­вет­ст­ву­ет аб­со­лют­но уп­ру­го­му У., 𝑘=0 – аб­со­лют­но не­уп­ру­го­му (пла­сти­че­ско­му) уда­ру.

Ко­сой У. ма­те­ри­аль­ной точ­ки об аб­со­лют­но уп­ру­гую глад­кую плос­кость опи­сы­ва­ет­ся пра­ви­лом «угол па­де­ния α ра­вен уг­лу от­ра­же­ния β». Ес­ли же ме­ж­ду точ­кой и плос­ко­стью воз­ни­ка­ет су­хое тре­ние с ко­эф. тре­ния f, то при ма­лом уг­ле па­де­ния в про­цес­се У. те­ря­ет­ся часть про­доль­ной ско­ро­сти. В этом слу­чае α < β, ес­ли ctg α > f > 0. При ctg α < f в не­ко­то­рых слу­ча­ях ма­те­ри­аль­ная точ­ка мо­жет да­же от­ра­зить­ся на­зад (т. к. де­фор­ма­ция про­ис­хо­дит не толь­ко по нор­ма­ли к по­верх­но­сти кон­так­та, но и по ка­са­тель­ной).

В клас­сич. тео­рии У. вво­дит­ся по­ня­тие удар­но­го им­пуль­са, оп­ре­де­ляю­ще­го из­ме­не­ние ко­ли­че­ст­ва дви­же­ния за вре­мя У. (из­ме­не­ни­ем по­ло­же­ния тел в те­че­ние У. пре­неб­ре­га­ют). Ес­ли те­ло не­сво­бод­но, то об­щие тео­ре­мы тео­рии У. по­зво­ля­ют оп­ре­де­лить так­же удар­ные ре­ак­ции свя­зей.

Для оп­ре­де­ле­ния вре­ме­ни У., удар­ных сил, на­пря­же­ний и де­фор­ма­ций не­об­хо­ди­мо учи­ты­вать ме­ха­нич. свой­ст­ва ма­те­риа­лов тел, их из­ме­не­ния в про­цес­се У., ха­рак­тер на­чаль­ных и гра­нич­ных ус­ло­вий. Наи­бо­лее раз­ра­бо­та­на тео­рия У. аб­со­лют­но уп­ру­гих тел, ма­те­ри­ал ко­торых под­чи­ня­ет­ся за­ко­нам уп­ру­го­сти тео­рии, по­зво­ляю­щей, напр., оце­нить до­лю энер­гии, рас­хо­дуе­мую на воз­бу­ж­де­ние внутр. уп­ру­гих волн.

Мо­де­ли­ро­ва­ние У. не впол­не уп­ру­гих тел тре­бу­ет учё­та свойств пла­стич­но­сти и/или вяз­ко­уп­ру­го­сти ма­те­риа­лов. В этой об­лас­ти ши­ро­ко ис­поль­зу­ет­ся эм­пи­рич. под­ход: ре­зуль­та­ты мно­го­числ. экс­пе­ри­мен­тов по­зво­ля­ют дать оцен­ки ха­рак­те­ри­стик ма­те­риа­ла в кон­крет­ных ус­ло­ви­ях У. (осо­бен­но при боль­ших ско­ро­стях). В не­ко­то­рых слу­ча­ях (напр., при У. вра­щаю­ще­го­ся мя­ча об пол) не­об­хо­дим рас­чёт не толь­ко ве­ли­чи­ны нор­маль­ной со­став­ляю­щей удар­но­го им­пуль­са, но и ве­ли­чи­ны его ка­са­тель­ной со­став­ляю­щей, воз­ни­каю­щей за счёт тре­ния при У. Осо­бый слу­чай пред­став­ля­ет со­бой У. тре­ни­ем (см. в ст. Тре­ние внеш­нее).