НЕБЕ́СНЫЕ КООРДИНА́ТЫ

НЕБЕ́СНЫЕ КООРДИНА́ТЫ, чис­ла, опи­сы­ваю­щие по­ло­же­ние све­ти­ла на не­бес­ной сфе­ре. Как пра­ви­ло, ис­поль­зу­ют сфе­рич. сис­те­мы ко­ор­ди­нат, в ко­то­рых по­ло­же­ние на за­дан­ной сфе­ре опи­сы­ва­ет­ся дву­мя уг­ло­вы­ми ве­ли­чи­на­ми. Ес­ли рас­стоя­ния до све­тил из­вест­ны, то при­ме­ни­мы так­же де­кар­то­вы сис­те­мы ко­ор­ди­нат, но обыч­но вме­сто рас­стоя­ния ука­зы­ва­ет­ся па­рал­лакс не­бес­но­го све­ти­ла. При вы­со­ко­точ­ных из­ме­ре­ни­ях тре­бу­ет­ся учи­ты­вать эф­фек­ты об­щей тео­рии от­но­си­тель­но­сти. В этом слу­чае по­ло­же­ние све­ти­ла опи­сы­ва­ет­ся от­но­си­тель­но сис­тем от­счёта, яв­ляю­щих­ся со­во­куп­но­стью ко­ор­ди­нат­ных осей и шка­лы вре­ме­ни (вре­мя рас­смат­ри­ва­ет­ся как чет­вёр­тая ко­ор­ди­на­та не­бес­но­го те­ла).

В за­ви­си­мо­сти от вы­бо­ра на­ча­ла от­счё­та раз­ли­ча­ют сле­дую­щие сис­те­мы Н. к.: то­по­цен­три­че­ские (на­блю­да­тель на­хо­дит­ся на по­верх­но­сти Зем­ли), гео­цен­три­че­ские (на­блю­да­тель – в цен­тре масс Зем­ли), ба­ри­цен­три­че­ские (на­блю­да­тель – в цен­тре масс Сол­неч­ной сис­те­мы) и объ­ек­то­цен­три­че­ские (на­блю­да­тель – в цен­тре масс пла­не­ты, спут­ни­ка и т. п.). Со­от­вет­ст­вен­но в ка­ж­дой сис­теме оп­ре­де­ля­ют­ся шка­лы вре­ме­ни, т. е. вре­мен­нáя ко­ор­ди­на­та. Ма­те­ма­тич. оп­ре­де­ле­ние сис­тем Н. к. и свя­зи ме­ж­ду ни­ми, а так­же оп­ре­де­ле­ние шкал вре­ме­ни и со­от­но­ше­ний ме­ж­ду ни­ми яв­ля­ет­ся за­да­чей сфе­ри­че­ской ас­тро­но­мии. Реа­ли­за­ция сис­тем ко­ор­ди­нат, т. е. при­вяз­ка их к вы­бран­ным не­бес­ным те­лам, – за­да­ча ас­т­ро­мет­рии.

Для оп­ре­де­ле­ния сис­те­мы ко­ор­ди­нат не­об­хо­ди­мо за­дать её на­ча­ло (как пра­ви­ло, это по­ло­же­ние на­блю­да­те­ля) и на­прав­ле­ние осей. За­тем вы­би­ра­ет­ся осн. плос­кость сис­те­мы, про­хо­дя­щая че­рез на­ча­ло ко­ор­ди­нат. От осн. плос­ко­сти от­счи­ты­ва­ет­ся од­на из сфе­рич. ко­ор­ди­нат. Сис­те­мы ко­ор­ди­нат, при­ме­няе­мые в ас­тро­но­мии, по­лу­чи­ли на­зва­ния по осн. плос­ко­сти сис­те­мы: го­ри­зон­таль­ная, эк­ва­то­ри­аль­ная, эк­лип­ти­че­ская и га­лак­ти­че­ская.

Горизонтальная система координат

Системы небесных координат: а – горизонтальная, б – экваториальная, в – эклиптическая, г – галактическая. N, S, W, E – точки севера, юга, запада, востока; Z – зенит...

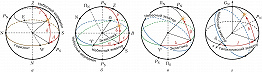
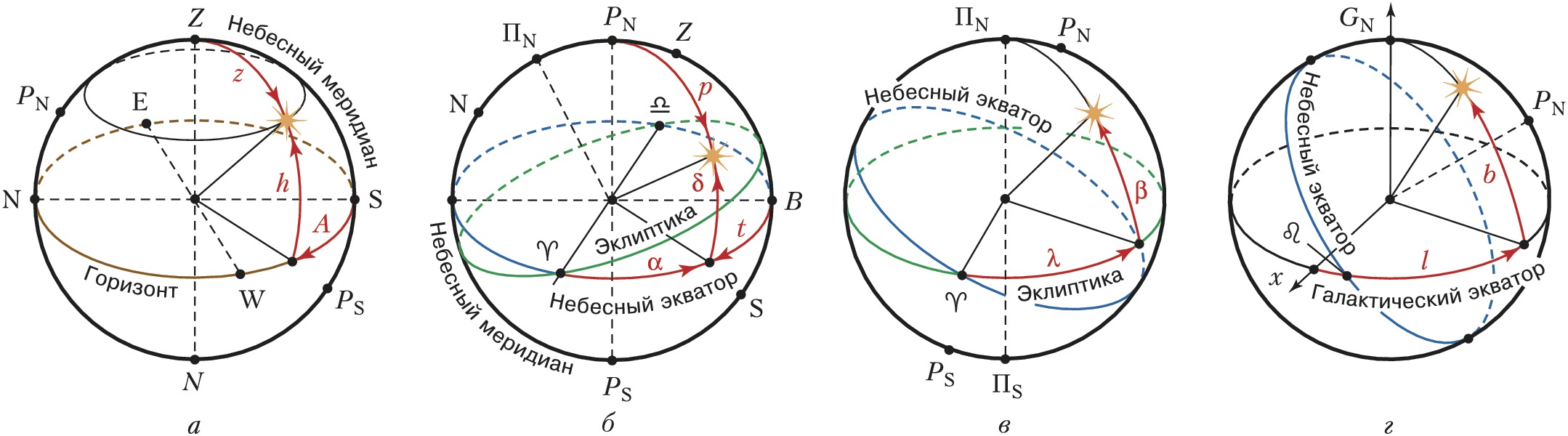
Вы­бран­ным на­прав­ле­ни­ем в этой сис­те­ме яв­ля­ет­ся на­прав­ле­ние от­вес­ной ли­нии; осн. плос­кость сис­те­мы пер­пен­ди­ку­ляр­на от­вес­ной ли­нии. Н. к. све­ти­ла в этой сис­те­ме яв­ля­ют­ся зе­нит­ное рас­стоя­ние $z$ и ази­мут $A$ (рис., а). Вме­сто $z$ час­то ис­поль­зу­ет­ся др. ко­ор­ди­на­та: вы­со­та $h$ све­ти­ла над го­ри­зон­том, при­чём $z+h=90°$. Ес­ли све­ти­ло на­хо­дит­ся над го­ри­зон­том, то его зе­нит­ное рас­стоя­ние из­ме­ня­ет­ся от 0° (све­ти­ло в зе­ни­те) до 90° (све­ти­ло в плос­ко­сти го­ри­зон­та). Ес­ли $z>90°$ ($h<0°$), то го­во­рят, что све­ти­ло на­хо­дит­ся под го­ри­зон­том; в этом слу­чае оно, как пра­ви­ло, не­ви­ди­мо для на­блю­да­те­ля.

Под ази­му­том в ас­тро­но­мии по­ни­ма­ет­ся дву­гран­ный угол ме­ж­ду вер­ти­каль­ным кру­гом, про­хо­дя­щим че­рез точ­ки се­ве­ра $N$ и юга $S$ (не­бес­ным ме­ри­диа­ном), и вер­ти­ка­лом све­ти­ла. Ази­мут мо­жет от­счи­ты­вать­ся от точ­ки юга $S$ в на­прав­ле­нии на за­пад $W$ (по ча­со­вой стрел­ке) от 0° до 360° или от точ­ки се­ве­ра $N$ на вос­ток $E$ от 0° до 360°; ино­гда ази­мут из­ме­ря­ет­ся в пре­де­лах от –180° до 180°.

Экваториальная система координат

Осн. плос­кость сис­те­мы – плос­кость не­бес­но­го эк­ва­то­ра, пер­пен­ди­ку­ляр­ная оси вра­ще­ния Зем­ли. Н. к. све­ти­ла в этой сис­те­ме яв­ля­ют­ся скло­не­ние $δ$ и пря­мое вос­хо­ж­де­ние $α$ (рис., б).

Скло­не­ние $δ$ от­счи­ты­ва­ет­ся от плос­ко­сти не­бес­но­го эк­ва­то­ра; $δ$ по­ло­жи­тель­но, ес­ли све­ти­ло на­хо­дит­ся в Сев. по­лу­ша­рии не­бес­ной сфе­ры, и от­ри­ца­тель­но, ес­ли – в Юж­ном, т. е. из­ме­ня­ет­ся в пре­де­лах от –90° до 90°. Ино­гда вме­сто скло­не­ния ис­поль­зу­ет­ся по­ляр­ное рас­стоя­ние $p$, ко­то­рое от­счи­ты­ва­ет­ся от сев. по­лю­са ми­ра $P_N$ и из­ме­ня­ет­ся в пре­де­лах от 0° до 180°, при­чём $p + \delta$ = 90°.

Вы­бор на­ча­ла от­счё­та пря­мых вос­хо­ж­де­ний про­из­во­лен, т. к. в плос­ко­сти не­бес­ного эк­ва­то­ра нет ни­ка­ко­го вы­де­лен­но­го на­прав­ле­ния. Пря­мое вос­хо­ж­де­ние от­счи­ты­ва­ет­ся от точ­ки ве­сен­не­го рав­но­ден­ст­вия ♈ про­тив ча­со­вой стрел­ки, ес­ли смот­реть с сев. по­лю­са ми­ра, и из­ме­ня­ет­ся в пре­де­лах от 0^h до 24^h или от 0° до 360°.

В 1998 Ме­ж­ду­нар. ас­тро­но­мич. сою­зом в ос­но­ву оп­ре­де­ле­ния Н. к. све­ти­ла был по­ло­жен ка­та­лог вне­га­лак­тич. ра­дио­ис­точ­ни­ков. За на­ча­ло от­счё­та пря­мых вос­хо­ж­де­ний взя­та точ­ка, близ­кая к ди­на­мич. рав­но­ден­ст­вию на эпо­ху J2000,0 (это сде­ла­но под­гон­кой пря­мо­го вос­хож­де­ния ква­за­ра 3C273B к зна­че­нию в сис­те­ме фун­дам. ка­та­ло­га FK5). При та­ком оп­ре­де­ле­нии точ­ка ве­сен­не­го рав­но­ден­ст­вия уже не при­вя­за­на к по­ло­же­нию эк­лип­ти­ки; её ста­биль­ность в про­стран­ст­ве объ­яс­ня­ет­ся от­сут­ст­ви­ем соб­ст­вен­но­го дви­же­ния ква­за­ров (из-за их уда­лён­но­сти).

В ка­че­ст­ве вто­рой ко­ор­ди­на­ты в этой сис­те­ме мо­жет ис­поль­зо­вать­ся ча­со­вой угол $t$, от­счи­ты­вае­мый от наи­выс­шей точ­ки $B$ не­бес­но­го эк­ва­то­ра по ча­со­вой стрел­ке, ес­ли смот­реть с сев. по­лю­са ми­ра, и из­ме­няю­щий­ся в тех же пре­де­лах, что и $α$. Сис­те­ма ко­ор­ди­нат, за­да­вае­мая ча­со­вым уг­лом и скло­не­ни­ем, яв­ля­ет­ся ле­вой.

Эклиптическая система координат

Эту сис­те­му ко­ор­ди­нат ис­поль­зу­ют, как пра­ви­ло, при изу­че­нии дви­же­ния тел Сол­неч­ной сис­те­мы, т. к. плос­ко­сти ор­бит боль­шин­ст­ва тел Сол­неч­ной сис­те­мы на­кло­не­ны к плос­ко­сти эк­лип­ти­ки под ма­лы­ми уг­ла­ми. Осн. кру­га­ми в эк­лип­тич. сис­те­ме ко­ор­ди­нат (рис., в) яв­ля­ют­ся плос­кость эк­лип­ти­ки и круг ши­ро­ты (боль­шой круг не­бес­ной сфе­ры, про­хо­дя­щий че­рез северный $П_N$ и южный $П_S$ по­лю­сы эк­лип­ти­ки и све­ти­ло). Н. к. све­ти­ла в этой сис­те­ме яв­ля­ют­ся эк­лип­тич. ши­ро­та и дол­го­та. Эк­лип­тич. ши­ро­та $β$ – это ду­га кру­га ши­ро­ты, от­счи­ты­вае­мая от плос­ко­сти эк­лип­ти­ки до све­ти­ла; она по­ло­жи­тель­на в Се­вер­ном и от­ри­ца­тель­на в Юж. по­лу­ша­рии не­бесной сфе­ры: $–90°⩽β⩽90°$. Эк­лип­тич. дол­го­та $λ$ – это дву­гран­ный угол ме­ж­ду боль­шим кру­гом, про­хо­дя­щим че­рез по­лю­сы эк­лип­ти­ки и точ­ку ве­сен­не­го рав­но­ден­ст­вия, и кру­гом ши­ро­ты. Дол­го­та от­счи­ты­ва­ет­ся от точ­ки ве­сен­не­го рав­но­ден­ст­вия про­тив ча­со­вой стрел­ки, ес­ли смот­реть с сев. по­лю­са эк­лип­ти­ки: $0°⩽λ⩽360°$.

Галактическая система координат

Эта сис­те­ма ко­ор­ди­нат час­то ис­поль­зу­ет­ся в за­да­чах звёзд­ной ди­на­ми­ки. За осн. плос­кость сис­те­мы при­ня­та плос­кость га­лак­тич. дис­ка; её по­ло­же­ние за­да­ёт­ся ко­ор­ди­на­та­ми од­но­го из по­лю­сов га­лак­ти­ки. В на­стоя­щее вре­мя га­лак­тич. сис­те­ма ко­ор­ди­нат оп­ре­де­ля­ет­ся по дан­ным, по­лу­чен­ным кос­мич. мис­си­ей Hipparcos (Ев­роп. кос­мич. агент­ст­во, 1989–93), по­зво­лив­шей оп­ре­де­лить ас­т­ро­мет­рич. па­ра­мет­ры 118 тыс. звёзд. Сев. по­люс Га­лак­ти­ки $G_N$ (рис., г) на эпо­ху J2000,0 име­ет сле­дую­щие эк­ва­то­ри­аль­ные ко­орди­на­ты: $α=192,85948°$, $δ=27,12825°$; диа­мет­раль­но про­ти­во­по­лож­ная точ­ка не­бес­ной сфе­ры счи­та­ет­ся юж. по­лю­сом Га­лак­ти­ки. Боль­шой круг, пер­пен­ди­ку­ляр­ный ли­нии, со­еди­няю­щей по­лю­сы, на­зы­ва­ет­ся га­лак­тич. эк­ва­то­ром. Боль­шой круг, про­хо­дя­щий че­рез све­ти­ло и по­лю­сы Га­лак­ти­ки, на­зы­ва­ет­ся кру­гом га­лак­тич. ши­ро­ты. Ду­га это­го кру­га от эк­ва­то­ра до све­ти­ла на­зы­ва­ет­ся га­лак­тич. ши­ро­той $b$ све­ти­ла. Га­лак­тич. ши­ро­та по­ло­жи­тель­на в Сев. по­лу­ша­рии (со­дер­жа­щем точ­ку $G_N$) и от­ри­ца­тель­на в Юж­ном: $–90°⩽b⩽90°$. Га­лак­тич. дол­го­та $l$ ра­нее от­счи­ты­ва­лась от точ­ки пе­ре­се­че­ния га­лак­тич. и не­бес­но­го эк­ва­то­ров ♌ , пря­мое вос­хо­ж­де­ние ко­то­рой рав­ня­лось $18^h40^m$. Ны­не га­лак­тич. дол­го­та от­счи­ты­ва­ет­ся от на­прав­ле­ния на центр Га­лак­ти­ки (на­прав­ле­ние х на рис., г), ко­то­рое оп­ре­де­ля­ет­ся че­рез га­лак­тич. дол­го­ту вос­хо­дя­ще­го уз­ла га­лак­тич. эк­ва­то­ра, рав­ную $l_♌=32,93192°$. Га­лак­тич. дол­го­та от­счи­ты­ва­ет­ся от 0° до 360° про­тив ча­со­вой стрел­ки, ес­ли смот­реть с сев. по­лю­са Га­лак­ти­ки.

Объектоцентрические системы координат

Эти сис­те­мы ис­поль­зу­ют при про­ве­де­нии на­блю­де­ний с др. пла­не­ты, с бор­та кос­мич. ап­па­ра­та или лю­бо­го др. те­ла. Осн. плос­кость сис­те­мы и её по­лю­сы свя­зы­ва­ют с тем те­лом, с ко­то­ро­го про­во­дят­ся на­блю­де­ния. Как пра­ви­ло, это плос­кость ор­би­ты или плос­кость эк­ва­то­ра (пер­пен­ди­ку­ляр­ная оси вра­ще­ния те­ла). Сис­те­ма ко­ор­ди­нат мо­жет так­же за­да­вать­ся ося­ми сис­те­мы ста­би­ли­за­ции кос­мич. ап­па­ра­та. Од­на из ко­ор­ди­нат, напр. ор­ди­на­та, есть ду­га боль­шо­го кру­га (кру­га ор­ди­нат), про­хо­дя­ще­го че­рез по­лю­сы сис­те­мы и све­ти­ло, от осн. плос­ко­сти до све­ти­ла. Вто­рая ко­ор­ди­на­та (абс­цис­са) – это дву­гран­ный угол ме­ж­ду боль­шим кру­гом, про­хо­дя­щим че­рез по­лю­сы сис­те­мы и точ­ку на­ча­ла от­счё­та абс­цисс, и кру­гом ор­ди­нат. Вы­бор на­ча­ла от­счё­та абс­цисс в прин­ци­пе про­из­во­лен и про­из­во­дит­ся с учё­том удоб­ст­ва об­ра­бот­ки на­блю­де­ний.