ВЯЗКОУПРУ́ГОСТЬ

ВЯЗКОУПРУ́ГОСТЬ в ме­ха­ни­ке твёр­до­го де­фор­ми­руе­мо­го те­ла, один из ви­дов по­ве­де­ния ма­те­риа­ла под на­груз­кой, при ко­то­ром од­но­вре­мен­но про­яв­ля­ют­ся свой­ст­ва, ха­рак­тер­ные как для уп­ру­го­го те­ла, так и для вяз­кой жид­ко­сти. Для уп­ру­го­го те­ла ме­ха­нич. на­пря­же­ние $σ$ про­пор­цио­наль­но де­фор­ма­ции (от­но­си­тель­но­му уд­ли­не­нию) $ε$: $σ=Eε$, где $E$ – мо­дуль уп­ру­го­сти (за­кон Гу­ка). Для вяз­кой жид­ко­сти на­пря­же­ние про­пор­цио­наль­но ско­ро­сти де­фор­ми­ро­ва­ния $\dot{\varepsilon}=\frac{d\varepsilon}{dt}\sigma=η\dot{\varepsilon}$, где $η$  – ко­эф. ди­на­мич. вязко­сти (со­от­но­ше­ние Нью­то­на). Де­фор­ми­ро­ва­ние вяз­ко­уп­ру­го­го те­ла в про­стей­ших слу­ча­ях ка­че­ст­вен­но опи­сы­ва­ет­ся рео­ло­гич. урав­не­ни­ем Мак­свел­ла:$$\dot{\varepsilon}=\frac{1}{E}\dot{\sigma}+\frac{1}{\eta}\sigma \qquad (1)$$

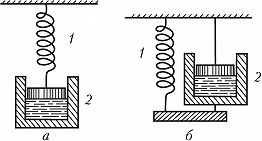
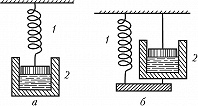
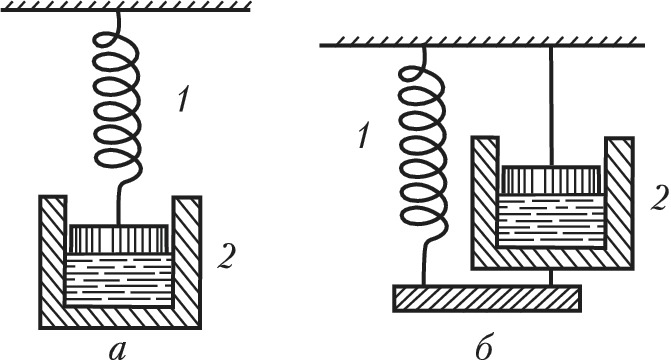
Эти урав­не­ния со­от­вет­ст­ву­ют ком­би­ни­ро­ван­ным ме­ха­нич. мо­де­лям, в ко­то­рых об­ра­зец из вяз­ко­уп­ру­го­го ма­те­риа­ла пред­став­ля­ет­ся в ви­де двух по­сле­до­ва­тель­но [урав­не­ние (1), мо­дель Мак­свел­ла, рис. 1а] или па­рал­лель­но [урав­не­ние (2), мо­дель Кель­ви­на – Фойх­та, рис. 1б] со­еди­нён­ных эле­мен­тов – уп­ру­гой пру­жины и вяз­ко­го демп­фе­ра, пред­став­ляю­ще­го со­бой пор­шень в ци­лин­д­ре, за­пол­нен­ном вяз­кой жид­ко­стью (мас­лом). При дви­же­нии порш­ня вяз­кая жид­кость про­са­чи­ва­ет­ся че­рез уз­кий за­зор ме­ж­ду пор­ш­нем и стен­кой ци­лин­д­ра, что и обес­пе­чи­ва­ет вяз­кое со­про­тив­ле­ние дви­же­нию. Ли­ней­ные урав­не­ния ти­па (1) и (2) при­ме­ни­мы толь­ко при дос­та­точ­но не­боль­ших ме­ха­нич. на­пря­же­ни­ях. В боль­шин­ст­ве слу­ча­ев тре­бу­ет­ся ис­поль­зо­ва­ние слож­ных не­ли­ней­ных урав­не­ний.

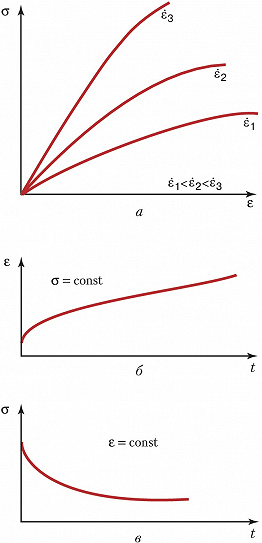
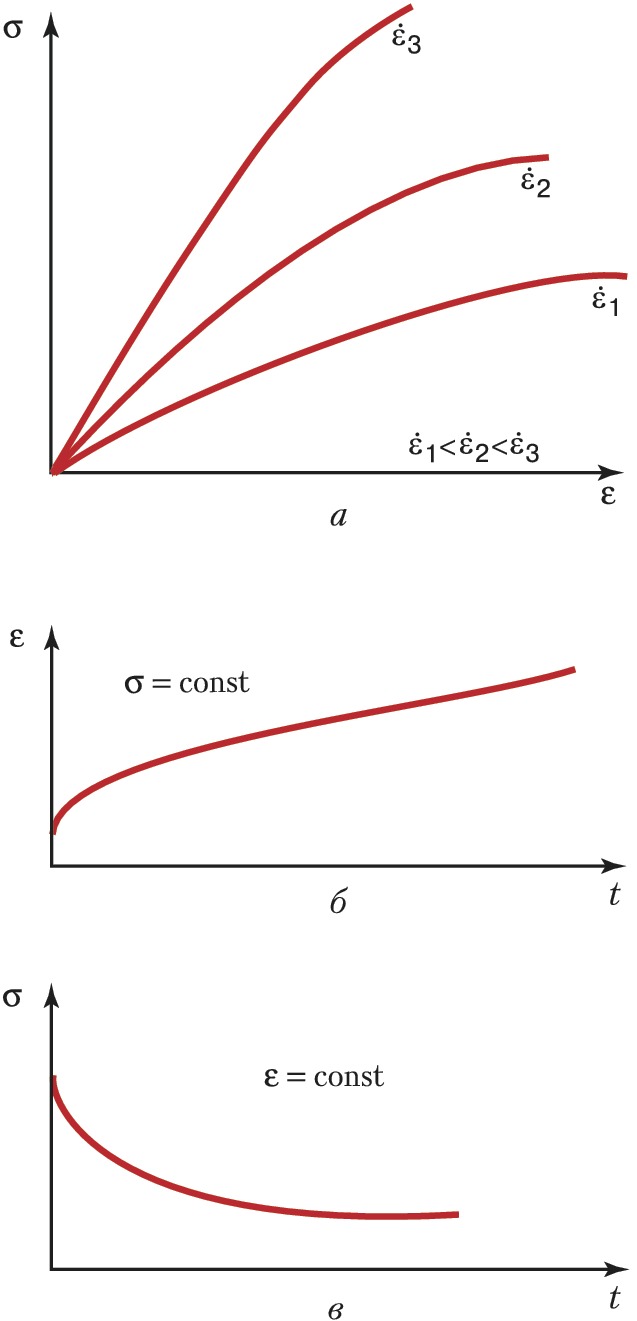
При рас­тя­же­нии ци­лин­д­рич. об­раз­ца вяз­ко­уп­ру­гие свой­ст­ва про­яв­ля­ют­ся как силь­ное влия­ние ско­ро­сти де­фор­ми­ро­ва­ния $έ$ на за­ви­си­мость $σ$ от $ε$ (кри­вая рас­тя­же­ния, рис. 2а), уве­ли­че­ние со вре­ме­нем $t$ де­фор­ма­ции ε при по­сто­ян­ном на­пря­же­нии $σ$ (пол­зу­честь, рис. 2б), умень­ше­ние со вре­ме­нем $t $ на­пря­же­ния $σ$ в рас­тя­ну­том и за­фик­си­ро­ван­ном об­раз­це (ре­лак­са­ция, рис. 2в).

Рис. 1. Механические модели, качественно описывающие вязкоупругое поведение твёрдого тела: а – модель Максвелла с последовательным соединением пружины 1 и поршня в цилиндре 2; б – модель К...

Су­ще­ст­вую­щие мо­ле­ку­ляр­ные тео­рии да­ют лишь гру­бую, ка­че­ст­вен­ную кар­ти­ну ме­ха­низ­ма вяз­ко­уп­ру­го­го по­ве­де­ния твёр­до­го те­ла. В по­ли­ме­рах боль­шин­ст­во длин­ных цеп­ных мо­ле­кул на­хо­дит­ся в по­лу­свёр­ну­том со­стоя­нии; рас­тя­ги­ваю­щее на­пря­же­ние стре­мит­ся вы­пря­мить мо­ле­ку­лу и со­ри­ен­ти­ро­вать её па­рал­лель­но на­прав­ле­нию рас­тя­ги­ваю­щей си­лы. При этом часть мо­ле­кул бы­ст­ро дос­ти­га­ет та­ко­го со­стоя­ния, в то вре­мя как др. часть рас­прям­ля­ет­ся за­мед­лен­но (вы­со­ко­эла­сти­че­ская де­фор­ма­ция). Кро­ме то­го, мо­жет воз­ник­нуть те­че­ние ма­те­риа­ла, свя­зан­ное с про­скаль­зы­ва­ни­ем од­них це­пей мо­ле­кул от­но­си­тель­но дру­гих. В ре­зи­не и ре­зи­но­по­доб­ных эла­сто­ме­рах длин­ные цеп­ные мо­ле­ку­лы уло­же­ны ме­нее плот­но, чем в по­ли­ме­рах, по­это­му они мо­гут сви­вать­ся и рас­прям­лять­ся от­но­си­тель­но сво­бод­но, что и по­зво­ля­ет ре­зи­не вы­дер­жи­вать ог­ром­ные ме­ха­нич. де­фор­ма­ции.

Рис. 2. Вязкоупругие свойства цилиндрического образца при растяжении: а – влияние скорости деформирования έ на зависимость σ(ε); б – ползучесть; в – релаксация.

Ин­те­рес к вяз­ко­уп­ру­го­му по­ве­де­нию твёр­до­го те­ла свя­зан с ши­ро­ким ис­поль­зо­ва­ни­ем по­ли­ме­ров, пла­ст­масс, ас­фаль­то­вых по­кры­тий, твёр­до­го то­п­ли­ва ра­кет­ных дви­га­те­лей и др. Тео­рия В. яв­ля­ет­ся важ­ной ча­стью рео­ло­гии.