ПОЛЗУ́ЧЕСТЬ

ПОЛЗУ́ЧЕСТЬ (англ. creep) ма­те­риа­лов, за­ви­ся­щая от вре­ме­ни де­фор­ма­ция твёр­до­го те­ла под воз­дей­ст­ви­ем ме­ха­нич. на­пря­же­ния. В ме­ха­ни­ке де­фор­ми­руе­мо­го твёр­до­го те­ла ма­те­риа­лы при­ня­то раз­ли­чать по их ре­ак­ции на на­груз­ку. Ес­ли ци­лин­д­рич. об­ра­зец при про­из­воль­ном рас­тя­же­нии воз­вра­ща­ет­ся в ис­ход­ное со­стоя­ние сра­зу же по­сле сня­тия на­груз­ки, го­во­рят, что он из­го­тов­лен из уп­ру­го­го ма­те­риа­ла. Ес­ли по­сле раз­груз­ки по­яв­ля­ет­ся ос­та­точ­ная де­фор­ма­ция, ко­то­рая за­ви­сит толь­ко от ве­ли­чин на­гру­зок и по­ряд­ка их при­ло­же­ния (но не за­ви­сит от ско­ро­сти на­гру­же­ния и вре­ме­ни вы­держ­ки), ма­те­ри­ал на­зы­ва­ют уп­ру­го­пла­сти­че­ским. В слу­чае же, ко­гда де­фор­ма­ция су­ще­ст­вен­но за­ви­сит от дли­тель­но­сти на­гру­же­ния, го­во­рят, что ма­те­ри­ал об­ла­да­ет пол­зу­че­стью.

Все ма­те­риа­лы в оп­ре­де­лён­ном диа­па­зо­не на­пря­же­ний и тем­пе­ра­тур в той или иной ме­ре об­ла­да­ют П. Напр., кон­ст­рук­ци­он­ные ста­ли или алю­ми­ние­вые спла­вы об­на­ру­жи­ва­ют свой­ст­ва т. н. ог­ра­ни­чен­ной П. (при ко­то­рой де­фор­ма­ция с те­че­ни­ем вре­ме­ни асим­пто­ти­че­ски стре­мит­ся к ко­неч­но­му пре­де­лу) да­же при ком­нат­ной темп-ре. Осо­бен­но су­ще­ст­вен­на П. ме­тал­лич. кон­ст­рук­ций в ус­ло­ви­ях вы­со­ких тем­пе­ра­тур. Зна­че­ния тем­пе­ра­тур, при ко­то­рых не­об­хо­ди­мо учи­ты­вать П., за­мет­но раз­ли­ча­ют­ся для раз­ных ме­тал­лов. Так, для алю­ми­ние­вых спла­вов учёт П. во всём диа­па­зо­не на­пря­же­ний ва­жен уже при темп-рах 150–250 °C, для обыч­ных кон­ст­рук­ци­он­ных ста­лей – при темп-рах вы­ше 400 °C, для спец. жа­ро­проч­ных спла­вов – при темп-рах вы­ше 700–800 °C.

Зависимость деформации ε от времени t при постоянном напряжении для образца, обладающего ползучестью. Крестиком обозначена точка разрыва.

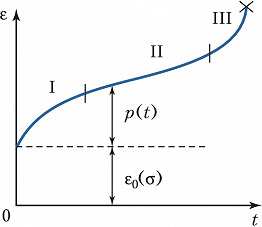
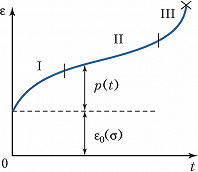
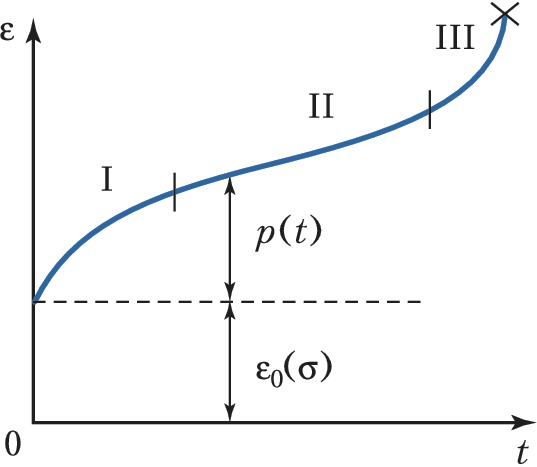
За­ви­си­мость де­фор­ма­ции ε рас­тя­ги­вае­мо­го об­раз­ца от вре­ме­ни t при по­сто­ян­ном на­пря­же­нии σ пред­став­ле­на на ри­сун­ке. При по­строе­нии этой кри­вой пред­по­ла­га­ет­ся, что дли­тель­ность на­гру­же­ния об­раз­ца до за­дан­но­го зна­че­ния σ очень ма­ла по срав­не­нию с про­дол­жи­тель­но­стью ис­пы­та­ния. По­это­му кри­вая за­ви­си­мо­сти ε(t) на­чи­на­ет­ся со зна­че­ния де­фор­ма­ции ε₀(σ ), со­от­вет­ст­вую­ще­го «мгно­вен­но­му» на­гру­же­нию. Раз­ность p=ε (t)-ε₀(σ ) на­зы­ва­ют де­фор­ма­ци­ей П. В об­щем слу­чае кри­вая ε(t) име­ет три чёт­ко вы­ра­жен­ных уча­ст­ка: I – уча­сток с по­сто­ян­но умень­шаю­щей­ся ско­ро­стью П. (не­ус­та­но­вив­шая­ся П.); II – уча­сток с по­сто­ян­ной (ми­ни­маль­ной) ско­ро­стью П. (ус­та­но­вив­шая­ся П.); III – уча­сток ус­ко­ряю­щей­ся П., пред­ше­ст­вую­щий раз­ру­ше­нию. При дос­та­точ­но ма­лых на­пря­же­ни­ях кри­вая ε(t) мо­жет иметь толь­ко уча­сток I, то­гда как на кри­вых, со­от­вет­ст­вую­щих дос­та­точ­но боль­шим на­пря­же­ни­ям, этот уча­сток мо­жет от­сут­ст­во­вать. Для опи­са­ния за­ви­си­мо­сти де­фор­ма­ции по­ли­ме­ров от вре­ме­ни час­то ис­поль­зу­ет­ся тео­рия на­след­ст­вен­ной пол­зу­че­сти.

Изу­че­ние П. ма­те­риа­ла по­зво­ля­ет ис­сле­до­вать про­цес­сы, про­те­каю­щие в ма­те­риа­ле при вы­со­ких темп-рах. Од­на­ко пол­ный учёт свойств ма­те­риа­лов при­во­дит к су­ще­ст­вен­но­му ус­лож­не­нию со­от­но­ше­ний, свя­зы­ваю­щих на­пря­же­ния, де­фор­ма­ции и вре­мя, и, со­от­вет­ст­вен­но, к су­ще­ст­вен­но­му ус­лож­не­нию кон­крет­ных ма­те­ма­тич. за­дач. За­да­ча тео­рии П. за­клю­ча­ет­ся в ус­та­нов­ле­нии свя­зи ме­ж­ду ве­ли­чи­на­ми σ, t, p и темп-рой Т; эта связь долж­на при про­из­воль­ных за­ко­нах из­ме­не­ния на­пря­же­ния σ(t) и темп-ры T(t) оп­ре­де­лять кри­вую пол­зу­че­сти p(t).

Прин­ци­пи­аль­но важ­ный вклад в раз­ви­тие тео­рии П. вне­сли Ю. Н. Ра­бот­нов, Ф. Од­квист (Шве­ция), Л. М. Ка­ча­нов и др. В 1960-х гг. Ра­бот­нов для опи­са­ния про­цес­са П. кон­ст­рук­ци­он­ных ма­те­риа­лов при од­но­ос­ном и слож­ном на­пря­жён­ных со­стоя­ни­ях пред­ло­жил ки­не­тич. тео­рию П. Со­глас­но этой тео­рии, ско­рость П. струк­тур­но ус­той­чи­во­го ма­те­риа­ла в ка­ж­дый мо­мент вре­ме­ни за­ви­сит от ве­ли­чин на­пря­же­ния и темп-ры, а так­же от струк­тур­но­го со­стоя­ния ма­те­риа­ла, ха­рак­те­ри­зуе­мо­го на­бо­ром ве­ли­чин, на­зы­вае­мых струк­тур­ны­ми па­ра­мет­ра­ми. Оп­ре­де­ляю­щие урав­не­ния тео­рии Ра­бот­но­ва вклю­ча­ют урав­не­ние ме­ха­нич. со­стоя­ния и сис­те­му ки­не­тич. урав­не­ний для оп­ре­де­ле­ния этих струк­тур­ных па­ра­мет­ров. Все тео­ре­тич. ис­сле­до­ва­ния, по­лу­чен­ные в ми­ре за по­след­ние пол­ве­ка, опи­ра­ют­ся на тео­рию Ра­бот­но­ва, раз­ви­ва­ют и кон­кре­ти­зи­ру­ют её.

П. ме­тал­лов не­ред­ко про­яв­ля­ет­ся в эле­мен­тах кон­ст­рук­ций, под­вер­гаю­щих­ся зна­чит. на­груз­кам при вы­со­ких темп-рах. Впер­вые учёт де­фор­ма­ций П. по­тре­бо­вал­ся на прак­ти­ке в нач. 20 в. при ана­ли­зе ра­бо­ты де­та­лей па­ро­вых тур­бин. П. мо­жет при­во­дить к раз­ру­ше­нию авиац. дви­га­те­лей, вы­зы­вать из­бы­точ­ные де­фор­ма­ции об­шив­ки ЛА при вы­со­ких ско­ро­стях по­лё­та. Осо­бые про­бле­мы вы­зы­ва­ет П. в эле­мен­тах ядер­ных энер­госи­ло­вых ус­та­но­вок в свя­зи с жё­ст­ки­ми тре­бо­ва­ния­ми безо­пас­но­сти. П. учи­ты­ва­ет­ся при про­ек­ти­ро­ва­нии сис­те­мы тер­мич. за­щи­ты КА. В тех­но­ло­гич. про­цес­сах (про­кат­ка, штам­пов­ка и др.) пер­спек­тив­но ис­поль­зо­ва­ние вы­со­ко­тем­пе­ра­тур­но­го фор­мо­из­ме­не­ния за­го­то­вок в ус­ло­ви­ях П. Боль­шое зна­че­ние име­ет при­ме­не­ние тео­рии П. при раз­ра­бот­ке ме­то­дов рас­чё­та не­пре­рыв­ной раз­лив­ки ста­ли.