ПЕРКОЛЯ́ЦИЯ

Рис. 1. Эволюция структуры перколяционной золотой плёнки на стеклянной подложке при увеличении концентрации золота; при достижении порога перколяции канал из золота проходит через всю плёнку.

ПЕРКОЛЯ́ЦИЯ (про­те­ка­ние) (от лат. per­colo – про­са­чи­вать­ся, про­те­кать), воз­ни­ка­ет в двух- или мно­го­фаз­ных сис­те­мах при при­бли­же­нии к не­ко­то­рой кри­тич. кон­цен­тра­ции (т. н. по­ро­гу П.). Та­ки­ми сис­те­ма­ми мо­гут быть разл. при­род­ные сис­те­мы и спе­ци­аль­но при­го­тов­лен­ные ма­те­риа­лы. В тер­ми­нах П. мож­но опи­сать са­мые раз­ные яв­ле­ния, та­кие как про­те­ка­ние во­ды че­рез по­рис­тые ма­те­риа­лы, про­хо­ж­де­ние га­за че­рез уголь­ные фильт­ры, из­ме­не­ние со­стоя­ния маг­не­ти­ков при вне­дре­нии в них не­маг­нит­ных час­тиц, про­хо­ж­де­ние элек­трич. то­ка че­рез со­во­куп­ность про­во­дя­щих и не­про­во­дя­щих эле­мен­тов, рас­про­стра­не­ние ин­фор­ма­ции, эпи­де­мий, лес­ных по­жа­ров и мн. др. По­ня­тие П. вве­де­но брит. учё­ны­ми Д. Брод­бен­том и Дж. Хам­мер­с­ли в 1957.

Осн. осо­бен­но­сти по­ве­де­ния разл. при­род­ных сис­тем и спе­ци­аль­но при­го­тов­лен­ных ма­те­риа­лов вбли­зи по­ро­га П. мо­гут быть по­ня­ты на ос­но­ве сле­дую­щей про­стой мо­де­ли. Да­на ку­бич. или квад­рат­ная ре­шёт­ка из свя­зей, слу­чай­ная часть ко­то­рых про­во­дя­щая («чёр­ная»), а ос­таль­ная часть («бе­лая») – не­про­во­дя­щая (ра­зо­рван­ные свя­зи); «чёр­ные» свя­зи про­во­дят элек­трич. ток, «бе­лые» – не про­во­дят. Не­об­хо­ди­мо най­ти та­кую ми­ним. кон­цен­тра­цию «чёр­ных» свя­зей, при ко­то­рой ещё есть путь по «чёр­ным» свя­зям че­рез всю ре­шёт­ку. Та­кую кри­тич. кон­цен­тра­цию и на­зы­ва­ют по­ро­гом П. Свой­ст­ва сис­те­мы кар­ди­наль­но из­ме­ня­ют­ся при пе­ре­хо­де че­рез по­рог П. Су­ще­ст­во­ва­ние по­ро­га П. – осн. свой­ст­во пер­ко­ля­ци­он­ных сис­тем.

Перколяционные металлические плёнки (ПМП)

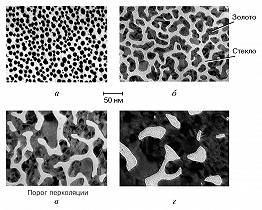
ПМП яв­ля­ют­ся раз­но­вид­но­стью ме­та­ма­те­риа­лов. Их по­лу­ча­ют пу­тём тер­мич. ис­па­ре­ния или на­пы­ле­ния ме­тал­ла на изо­ли­рую­щую (стек­лян­ную, квар­це­вую или сап­фи­ро­вую) под­лож­ку. При на­пы­ле­нии на под­лож­ке сна­чала фор­ми­ру­ют­ся мик­ро­ско­пич. ме­тал­лич. зёр­на раз­ме­ром в неск. на­но­мет­ров (рис. 1, а). По ме­ре за­пол­не­ния по­верх­но­сти ме­тал­лом про­ис­хо­дит сра­щи­ва­ние на­но­ча­стиц и на под­лож­ке фор­ми­ру­ют­ся ме­тал­лич. кла­сте­ры с не­ре­гу­ляр­ной струк­ту­рой (рис. 1, б). Кла­сте­ры со­еди­ня­ют­ся друг с дру­гом и об­ра­зу­ют всё бо­лее и бо­лее слож­ные струк­ту­ры, раз­мер ко­то­рых не­ог­ра­ни­чен­но уве­ли­чи­ва­ет­ся и, на­ко­нец, воз­ни­ка­ет не­пре­рыв­ный про­во­дя­щий ка­нал, про­хо­дя­щий че­рез всю плён­ку (рис. 1, в). До­ля пло­ща­ди плён­ки, за­ни­мае­мая ме­тал­лом в мо­мент об­ра­зо­ва­ния ка­на­ла про­те­ка­ния, на­зы­ва­ет­ся по­ро­гом П. плён­ки. При даль­ней­шем уве­ли­че­нии по­кры­тия по­верх­но­сти ме­тал­лом об­ра­зу­ет­ся сет­ка ка­на­лов про­те­ка­ния, и за­тем плён­ка ста­но­вит­ся ме­тал­ли­че­ской с не­ко­то­рым ко­ли­че­ст­вом пус­тот не­ре­гу­ляр­ной фор­мы (рис. 1, г), а да­лее – од­но­род­ной.

Рис. 2. Экспериментально измеренное распределение интенсивности света I в перколяционной золотой плёнке; I0 – интенсивность падающего света.

По­рог П. в ПМП мож­но оп­ре­де­лить, из­ме­рив элек­трич. со­про­тив­ле­ние ме­ж­ду дву­мя про­ти­во­по­лож­ны­ми сто­ро­на­ми об­раз­ца. При боль­шой кон­цен­тра­ции ме­та­лла, ко­гда плён­ка вы­гля­дит поч­ти как иде­аль­ное зер­ка­ло, со­про­тив­ле­ние со­от­вет­ст­ву­ет по­верх­но­ст­но­му со­про­тив­ле­нию ме­тал­ла. По ме­ре умень­ше­ния кон­цен­тра­ции ме­тал­ла со­про­тив­ле­ние уве­ли­чи­ва­ет­ся и прак­ти­че­ски об­ра­ща­ет­ся в бес­ко­неч­ность при кон­цен­тра­ции ме­тал­ла, со­от­вет­ст­вую­щей по­ро­гу П. При кон­цен­тра­ци­ях, мень­ших по­ро­га П., плён­ка ве­дёт се­бя как ди­элек­трик. В зо­ло­тых пер­ко­ля­ци­он­ных плён­ках по­ро­го­вая кон­цен­тра­ция ме­тал­ла со­став­ля­ет 40–60% (при­мер­но по­ло­ви­на по­верх­но­сти под­лож­ки по­кры­та зо­ло­том). Од­на­ко при та­кой боль­шой кон­цен­тра­ции ме­тал­ла элек­трич. со­про­тив­ле­ние ста­но­вит­ся бес­ко­неч­но боль­шим, по­сколь­ку вбли­зи по­ро­га П. элек­трич. ток те­чёт толь­ко по ка­на­лам про­те­ка­ния, об­ра­зую­щим слу­чай­ную сет­ку. Ха­рак­тер­ный раз­мер ячей­ки этой сет­ки (кор­ре­ля­ци­он­ная дли­на) уве­ли­чи­ва­ет­ся при при­бли­же­нии к по­ро­гу П. Сет­ка ка­на­лов про­те­ка­ния ста­но­вит­ся всё бо­лее круп­но­ячеи­стой, и, на­ко­нец, при дос­ти­же­нии по­ро­га П. она раз­ры­ва­ет­ся и элек­трич. со­про­тив­ле­ние всей сис­те­мы об­ра­ща­ет­ся в бес­ко­неч­ность.

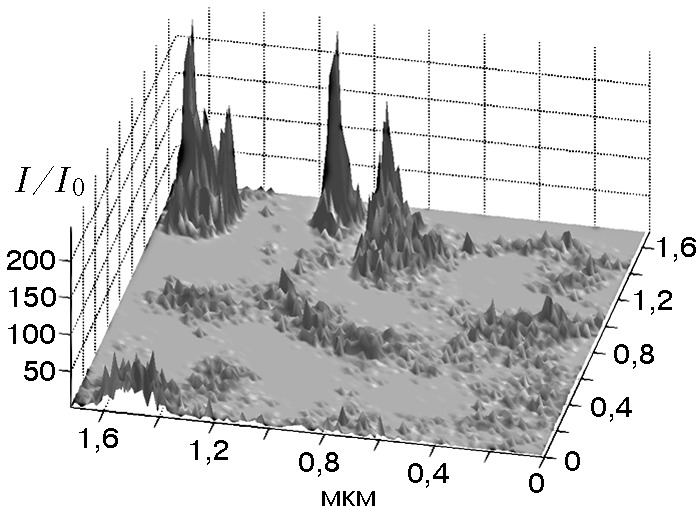
ПМП ши­ро­ко при­ме­ня­ют­ся в оп­тич. фильт­рах, кон­цен­тра­то­рах сол­неч­ной энер­гии и др. В кон. 20 в. об­на­ру­же­но, что флук­туа­ции ло­каль­ных оп­тич. по­лей в та­ких плён­ках дос­ти­га­ют ги­гант­ских мас­шта­бов и пре­вы­ша­ют ин­тен­сив­ность па­даю­ще­го све­та в сот­ни и ты­ся­чи раз (рис. 2). При­чи­на это­го в том, что ка­на­лы про­те­ка­ния ак­ку­му­ли­ру­ют энер­гию па­даю­ще­го све­та в ши­ро­ком спек­траль­ном диа­па­зо­не. Это яв­ле­ние ис­поль­зу­ет­ся для соз­да­ния вы­со­ко­чув­ст­ви­тель­ных хи­мич. и био­ло­гич. сен­со­ров.

Силь­ные флук­туа­ции ло­каль­ных элек­трич. по­лей при­во­дят к уси­ле­нию разл. не­ли­ней­ных эф­фек­тов. Не­ли­ней­ные пер­ко­ля­ци­он­ные ком­по­зи­ты мо­гут быть ис­поль­зо­ва­ны как сре­ды с по­ка­за­те­лем пре­лом­ле­ния, за­ви­ся­щим от ин­тен­сив­но­сти све­та, как не­ли­ней­ные фильт­ры и оп­тич. бис­та­биль­ные эле­мен­ты.

Протекание газа через угольный фильтр

По­хо­жим об­ра­зом ве­дёт се­бя про­ни­цае­мость уголь­но­го фильт­ра, в ко­то­ром воз­дух вме­сте с вред­ным га­зом про­хо­дит че­рез по­ры в уг­ле. Эти по­ры со­еди­ня­ют­ся друг с дру­гом, об­ра­зуя за­пу­тан­ный ла­би­ринт, со­стоя­щий из ка­на­лов про­те­ка­ния. Ес­ли по­ры дос­та­точ­но ши­ро­ки и хо­ро­шо свя­за­ны друг с дру­гом, то воз­дух вме­сте с вред­ным га­зом лег­ко про­ни­ка­ет в глубь уголь­но­го фильт­ра по сис­те­ме шун­ти­рую­щих ка­на­лов про­те­ка­ния. Про­те­ка­ние га­за по ла­би­рин­ту пред­став­ля­ет со­бой про­цесс, су­ще­ст­вен­но от­ли­чаю­щий­ся от яв­ле­ния диф­фу­зии. Сте­пень очи­ст­ки воз­ду­ха от вред­ных га­зов за­ви­сит от дли­ны пу­ти, по ко­то­ро­му про­хо­дит воз­дух (чем боль­ше этот путь, тем луч­ше бу­дет очи­щен воз­дух). При умень­ше­нии кон­цен­тра­ции пор сис­те­ма ка­на­лов про­те­ка­ния бу­дет всё мень­ше и мень­ше, а при даль­ней­шем умень­ше­нии и сам путь, по ко­то­ро­му те­чёт воз­дух, пре­рвёт­ся. Кри­тич. кон­цен­тра­ция пор и пред­став­ля­ет со­бой по­рог П. для дан­ной за­да­чи.

Распространение лесных пожаров

Пред­по­ло­жим, что лес по­са­жен в ви­де ре­гу­ляр­ной квад­рат­ной ре­шёт­ки и огонь мо­жет пе­ре­ки­нуть­ся толь­ко на бли­жай­шие де­ре­вья. В та­ком ле­су по­жар мо­жет сво­бод­но рас­про­стра­нять­ся, ох­ва­ты­вая все де­ре­вья. Что­бы обезо­па­сить лес от раз­ру­ши­тель­ных по­жа­ров, вы­ру­ба­ют слу­чай­но вы­бран­ные де­ре­вья. Воз­ни­ка­ет во­прос, ка­кая ми­ним. часть де­ревь­ев долж­на быть вы­руб­ле­на, что­бы лес­ной по­жар все­гда был ло­ка­ли­зо­ван. В та­кой за­да­че от­но­си­тель­ное чис­ло ос­тав­лен­ных де­ревь­ев долж­но быть не­мно­го мень­ше по­ро­га П. Сфор­му­ли­ро­ван­ная та­ким об­ра­зом за­да­ча на­зы­ва­ет­ся за­да­чей П. по уз­лам на квад­рат­ной ре­шёт­ке.

Теория перколяции

Эта тео­рия раз­ра­бо­та­на для ре­ше­ния за­да­чи о на­хо­ж­де­нии по­ро­га П. В тео­рии П. ус­лов­но мож­но вы­де­лить гео­мет­рич. и фи­зич. час­ти. Пер­вая изу­ча­ет струк­ту­ру, ста­ти­сти­ку, связ­ность «чёр­ных» и «бе­лых», ко­неч­ных и бес­ко­неч­ных кла­сте­ров в про­стран­ст­вах разл. раз­мер­но­сти. Вто­рая изу­ча­ет разл. фи­зич. про­цес­сы в мно­го­фаз­ных сре­дах при кон­цен­тра­ции, близ­кой к по­ро­гу П. Изу­ча­ют­ся осо­бен­но­сти оп­тич., маг­нит­ных свойств, про­те­ка­ния элек­трич. то­ка, прыж­ко­вой про­во­ди­мо­сти, тер­мо­элек­трич. яв­ле­ний, уп­ру­гих и не­уп­ру­гих де­фор­ма­ций, рас­про­стра­не­ния ин­фор­ма­ции, эпи­де­мий, лес­ных по­жа­ров и др.

Со­во­куп­ность «чёр­ных» свя­зей (уз­лов), свя­зы­ваю­щих «ле­вую» бес­ко­неч­ность с «пра­вой», на­зы­ва­ют бес­ко­неч­ным кла­сте­ром, ко­то­рый су­ще­ст­ву­ет при кон­цен­тра­ции «чёр­ных» свя­зей вы­ше по­ро­га П. и от­сут­ст­ву­ет при кон­цен­тра­ции «чёр­ных» свя­зей ни­же по­ро­га П. Воз­ник­но­ве­ние (за­ро­ж­де­ние) бес­ко­неч­но­го кла­сте­ра при пе­ре­хо­де кон­цен­тра­ции че­рез по­рог П. мож­но рас­смат­ри­вать как гео­мет­рич. ана­лог воз­ник­но­ве­ния но­во­го со­стоя­ния, ха­рак­те­ри­зую­ще­го­ся па­ра­мет­ром по­ряд­ка. При опи­са­нии фи­зич. яв­ле­ний важ­ную роль иг­ра­ют струк­ту­ра и свой­ст­ва бес­ко­неч­но­го кла­сте­ра. Они ха­рак­те­ри­зу­ют­ся, напр., чис­лом свя­зей (уз­лов), при­над­ле­жа­щих бес­ко­неч­но­му кла­сте­ру в объ­ё­ме с раз­ме­ром а. Чис­ло свя­зей в квад­рат­ной ре­шёт­ке (или в лю­бой др. пло­ской пе­рио­дич. ре­шёт­ке) с раз­ме­ром а про­пор­цио­наль­но пло­ща­ди ре­шёт­ки а²; для ку­би­че­ской или лю­бой др. объ­ём­ной ре­гу­ляр­ной ре­шёт­ки чис­ло свя­зей про­пор­цио­наль­но объ­ё­му а³. Ока­зы­ва­ет­ся, что чис­ло свя­зей (уз­лов), при­над­ле­жа­щих бес­ко­неч­но­му кла­сте­ру, про­пор­цио­наль­но раз­ме­ру а, воз­ве­дён­но­му в сте­пень d_f, ко­то­рую на­зы­ва­ют фрак­таль­ной раз­мер­но­стью. Ком­пь­ю­тер­ное мо­де­ли­ро­ва­ние по­ка­за­ло, что d_f=2,6 и d_f=1,9 со­от­вет­ст­вен­но для объ­ём­но­го и плос­ко­го бес­ко­неч­ных кла­сте­ров. Плот­ность бес­ко­неч­но­го кла­сте­ра убы­ва­ет с уве­ли­че­ни­ем его раз­ме­ра. Гео­мет­рич. объ­ек­ты, плот­ность ко­то­рых убы­ва­ет с уве­ли­че­ни­ем раз­ме­ра, на­зы­ва­ют­ся фрак­та­ла­ми. Фрак­таль­ная при­ро­да бес­ко­неч­но­го кла­сте­ра иг­ра­ет ре­шаю­щую роль в разл. не­обыч­ных фи­зич. яв­ле­ни­ях вбли­зи по­ро­га пер­ко­ля­ции.

В бес­ко­неч­ном кла­сте­ре мож­но вы­де­лить: 1) «ске­лет кла­сте­ра» – в слу­чае про­те­ка­ния то­ка по «чёр­ным» свя­зям это – то­ко­про­во­дя­щая часть; 2) «мёрт­вые кон­цы» – час­ти бес­ко­неч­но­го кла­сте­ра, по ко­то­рым не те­чёт ток; 3) «крас­ные» свя­зи – оди­ноч­ные свя­зи, рас­по­ло­жен­ные та­ким об­ра­зом, что при уда­ле­нии лю­бой из них ток пе­ре­ста­ёт течь по мак­ро­ско­пи­че­ски боль­шой час­ти бес­ко­неч­но­го кла­сте­ра; 4) «ос­тов» кла­сте­ра – сум­ма крат­чай­ших пу­тей от дан­но­го уз­ла до уз­лов на за­дан­ном рас­стоя­нии. Ка­ж­дая из этих ха­рак­те­ри­стик оп­ре­де­ля­ет­ся сво­ей фрак­таль­ной раз­мер­но­стью или сво­им кри­тич. ин­дек­сом. Разл. час­ти бес­ко­неч­но­го кла­сте­ра от­ве­ча­ют за те или иные ас­пек­ты фи­зич. про­цес­сов вбли­зи по­ро­га П. Напр., ске­лет кла­сте­ра – это сис­те­ма ка­на­лов про­те­ка­ния, и по­это­му фрак­таль­ная раз­мер­ность ске­ле­та оп­ре­де­ля­ет по­ве­де­ние про­во­ди­мо­сти вбли­зи по­ро­га пер­ко­ля­ции.

Для по­ни­ма­ния фи­зич. свойств ис­поль­зу­ют­ся разл. гео­мет­рич. мо­де­ли бес­ко­неч­но­го кла­сте­ра. К нач. 21 в. осн. струк­тур­ные свой­ст­ва пер­ко­ля­ци­он­ных сис­тем хо­ро­шо изу­че­ны, разл. фрак­таль­ные раз­мер­но­сти рас­счи­та­ны и из­ме­ре­ны и гео­мет­рич. тео­рия П. близ­ка к за­вер­ше­нию. Фи­зич. тео­рия П. про­дол­жа­ет ус­пеш­но раз­ви­вать­ся, по­сколь­ку син­те­зи­ру­ют­ся, ис­сле­ду­ют­ся и при­ме­ня­ют­ся всё бо­лее слож­ные на­но­ком­по­зи­ты и ме­та­ма­те­риа­лы и во мно­гих из них про­ис­хо­дит яв­ле­ние про­те­ка­ния.