КАНАЛИ́РОВАНИЕ ЗАРЯ́ЖЕННЫХ ЧАСТИ́Ц

Рис. 1. Траектории заряженных частиц в кристалле при угле падения θ1<θЛ (кривая а) и при θ1>θЛ (кривая б).

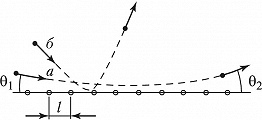
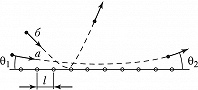
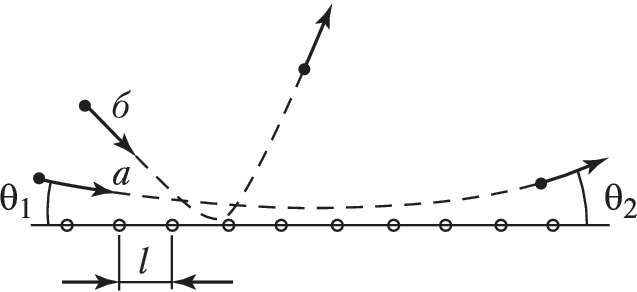
КАНАЛИ́РОВАНИЕ ЗАРЯ́ЖЕННЫХ ЧАС­ТИ́Ц, дви­же­ние за­ря­жен­ных час­тиц внут­ри мо­но­кри­стал­ла вдоль «ка­на­лов», об­ра­зо­ван­ных па­рал­лель­ны­ми ря­да­ми ато­мов или атом­ных плос­ко­стей. К. з. ч. бы­ло пред­ска­за­но амер. фи­зи­ка­ми М. Т. Ро­бин­со­ном и О. С. Оэном в 1961 и вско­ре экс­пе­ри­мен­таль­но об­на­ру­же­но в не­сколь­ких ла­бо­ра­то­ри­ях. Раз­ли­ча­ют ак­си­аль­ное и пло­ско­ст­ное К. з. ч. Ак­си­аль­ное К. з. ч. на­блю­да­ет­ся, ко­гда пу­чок бы­ст­рых за­ря­жен­ных час­тиц па­да­ет на мо­но­кри­сталл под ма­лым уг­лом $\textθ_1$ к од­ной из кри­стал­логра­фич. осей. При этом по­ло­жи­тель­но за­ря­жен­ная бы­ст­рая час­ти­ца (напр., про­тон), при­бли­жа­ясь к од­ной из це­по­чек ато­мов, па­рал­лель­ных кри­стал­ло­гра­фич. оси, в ре­зуль­та­те се­рии по­сле­до­ва­тель­ных ак­тов сла­бо­го рас­сея­ния на упо­ря­до­чен­но рас­по­ло­жен­ных ато­мах плав­но ис­крив­ля­ет свою тра­ек­то­рию так, что на­блю­да­ет­ся поч­ти зер­каль­ное от­ра­же­ние час­ти­цы от це­поч­ки ($\textθ_2=\textθ_1$; рис. 1, кри­вая а). Из тео­рии сле­ду­ет, что та­кого ро­да «зер­каль­ность» на­блю­да­ет­ся при $\textθ_1<\textθ_Л$, где $\textθ_Л$ – т. н. угол Линд­харда, ко­то­рый оп­ре­де­ля­ет­ся со­от­но­ше­ни­ем $\textθ_Л=\sqrt{Z_1Z_2e^2/ℰl}$, где $Z_1e, Z_2e$ – за­ря­ды дви­жу­щей­ся час­ти­цы и яд­ра ато­ма мо­но­кри­стал­ла, $ℰ$ – энер­гия час­ти­цы, $l$ – рас­стоя­ние ме­ж­ду со­сед­ни­ми ато­ма­ми в це­поч­ке. При та­ком дви­же­нии час­ти­ца удер­жи­ва­ет­ся вда­ли от ядер, на­хо­дя­щих­ся на оси це­поч­ки. При уве­ли­че­нии $\textθ_1$ до зна­че­ний $\textθ_1>\textθ_Л$ ха­рак­тер дви­же­ния из­ме­ня­ет­ся. Час­ти­ца мо­жет ис­пы­ты­вать близ­кие столк­но­ве­ния с яд­ра­ми, в ре­зуль­та­те ко­то­рых она рас­сеи­ва­ет­ся на боль­шой угол (рис. 1, кри­вая б) и да­лее дви­жет­ся так же, как в не­упо­ря­до­чен­ной сре­де. Угол $\textθ_Л$ обыч­но со­став­ля­ет ве­ли­чи­ну по­ряд­ка до­лей гра­ду­са. В тол­ще кри­стал­ла час­ти­ца, дви­жу­щая­ся в ре­жи­ме ак­си­аль­но­го каналирования, ис­пы­ты­ва­ет по­сле­до­ва­тель­ные ак­ты зер­каль­но­го от­ра­же­ния от раз­ных це­по­чек. В по­пе­реч­ной плос­ко­сти дви­же­ние та­кой час­ти­цы в об­щем слу­чае пред­став­ля­ет слу­чай­ное блу­ж­да­ние.

Пло­ско­ст­ное К. з. ч. на­блю­да­ет­ся при па­де­нии пуч­ка под ма­лым уг­лом к кри­с­тал­ло­гра­фич. плос­ко­сти. В этом слу­чае час­ти­цы по­пе­ре­мен­но от­ра­жа­ют­ся от со­сед­них плос­ко­стей; их тра­ек­то­рия на­по­ми­на­ет си­ну­сои­ду. При этом час­ти­ца так­же удер­жи­ва­ет­ся вда­ли от ядер.

Удер­жа­ние ка­на­ли­ро­ван­ных час­тиц вда­ли от ядер при­во­дит к ря­ду фи­зич. яв­ле­ний. Так, при $\textθ_1<\textθ_Л$ умень­ша­ет­ся вы­ход про­дук­тов ядер­ных ре­ак­ций и ха­рак­те­ри­стич. рент­ге­нов­ских лу­чей от внутр. элек­трон­ных обо­ло­чек. Ка­на­ли­ро­ван­ные час­ти­цы име­ют су­ще­ст­вен­но бóльшие про­бе­ги по срав­не­нию с час­ти­ца­ми, дви­жу­щи­ми­ся при от­сут­ст­вии ка­на­ли­ро­ва­ния.

Пер­во­на­чаль­но К. з. ч. на­блю­да­лось для пуч­ков по­ло­жи­тель­но за­ря­жен­ных от­но­си­тель­но тя­жё­лых час­тиц (про­то­нов, дей­тро­нов, α-час­тиц) при энер­гии по­ряд­ка 1 МэВ. В этом слу­чае из-за ма­ло­сти дли­ны вол­ны де Брой­ля ха­рак­тер дви­же­ния час­тиц прак­ти­че­ски яв­ля­ет­ся клас­си­че­ским.

Рис. 2. Поперечный периодический потенциал V для плоскостных каналов в случае позитронов (a) и электронов (б).

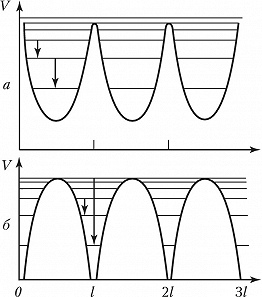
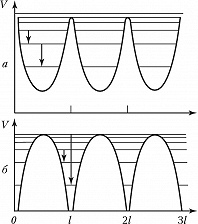
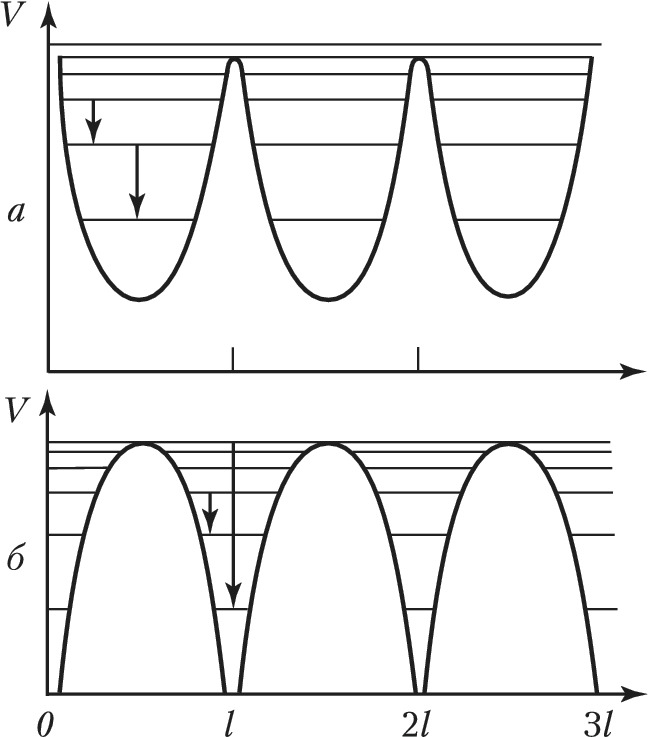
В слу­чае дви­же­ния бо­лее лёг­ких час­тиц (элек­тро­нов и по­зи­тро­нов) час­то су­ще­ст­вен­ны кван­то­вые эф­фек­ты. На рис. 2 па­ра­бо­ла­ми при­бли­жён­но изо­бра­же­на фор­ма по­пе­реч­но­го пе­рио­дич. по­тен­циа­ла $V$ для пло­ско­ст­ных ка­на­лов в слу­чае по­зи­тро­нов (рис. 2,а) и элек­тро­нов (рис. 2,б). Го­ри­зон­таль­ны­ми ли­ния­ми изо­бра­же­ны энер­ге­тич. уров­ни по­пе­реч­ной со­став­ляю­щей дви­же­ния час­тиц в кри­стал­ле. Стрел­ка­ми ука­за­ны не­ко­то­рые из воз­мож­ных кван­то­вых пе­ре­хо­дов. Со­от­вет­ст­вую­щие этим пе­ре­хо­дам ли­нии элек­тро­маг­нит­но­го из­лу­че­ния на­блю­да­ют­ся экс­пе­ри­мен­таль­но.

Рис. 3. Энергетический спектр рассеянных частиц при рассеянии на бездефектном кристалле (I); в кристалле, у которого на некоторой глубине располагается слой со значительным количеством дефектов (II); ...

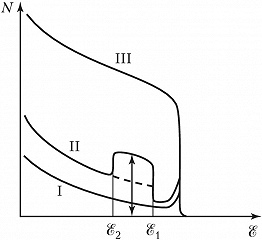
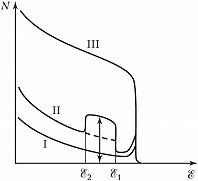
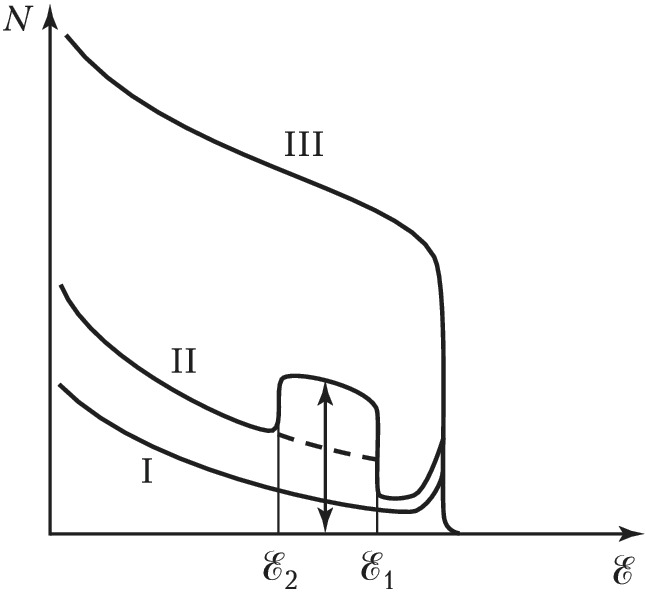
Од­но из при­ме­не­ний К. з. ч. – т. н. ме­тод об­рат­но­го рас­сея­ния на мо­но­кри­стал­лах. Пу­чок па­даю­щих час­тиц на­прав­ля­ет­ся вдоль кри­стал­ло­гра­фич. осей или плос­ко­стей, из­ме­ря­ет­ся энер­ге­тич. спектр про­дук­тов рас­сея­ния или ядер­ных ре­ак­ций. Лю­бые от­кло­не­ния от иде­аль­но­сти кри­стал­ла (тем­пе­ра­тур­ные ко­ле­ба­ния ато­мов, де­фек­ты) при­во­дят к ха­рак­тер­но­му ис­ка­же­нию энер­ге­тич. спек­тра (рис. 3). Ме­то­дом об­рат­но­го рас­сея­ния уда­ёт­ся экс­пе­ри­мен­таль­но оп­ре­де­лять по­ло­же­ние при­мес­ных ато­мов в ячей­ке кри­стал­ла, ис­сле­до­вать струк­ту­ру по­верх­но­ст­но­го слоя мо­но­кри­стал­ла и др.

С по­мо­щью К. з. ч. в изо­гну­тых кри­с­тал­лах уда­ёт­ся от­кло­нить пуч­ки час­тиц на не­боль­шие уг­лы при их вы­во­де из ус­ко­ри­те­лей. К. з. ч. мо­жет рас­смат­ри­вать­ся как ме­тод по­лу­че­ния мо­но­хро­ма­тич. пуч­ков γ-кван­тов разл. энер­гий. К. з. ч. не­об­хо­ди­мо учи­ты­вать при ион­ной им­план­та­ции, т. к. при оп­ре­де­лён­ных ус­ло­ви­ях оно мо­жет при­вес­ти к рас­ши­ре­нию им­план­ти­ро­ван­но­го слоя и ус­лож­не­нию его струк­ту­ры.

К. з. ч. от­но­сит­ся к груп­пе т. н. ори­ента­ци­он­ных эф­фек­тов, воз­ни­каю­щих при взаи­мо­дей­ст­вии бы­ст­рых за­ря­жен­ных час­тиц с кри­стал­ла­ми (см. так­же Те­ней эф­фект).