ДИСПЕ́РСИЯ ЗВУ́КА

Физическая дисперсия звука (зависимость скорости звука c от частоты ω ): c0 – скорость звука на частотах много меньших частоты релаксации ωр; с∞ – скорость звука на часто...

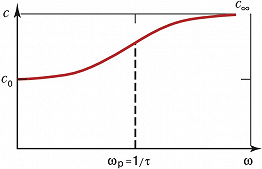
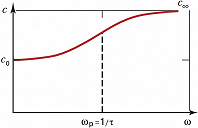
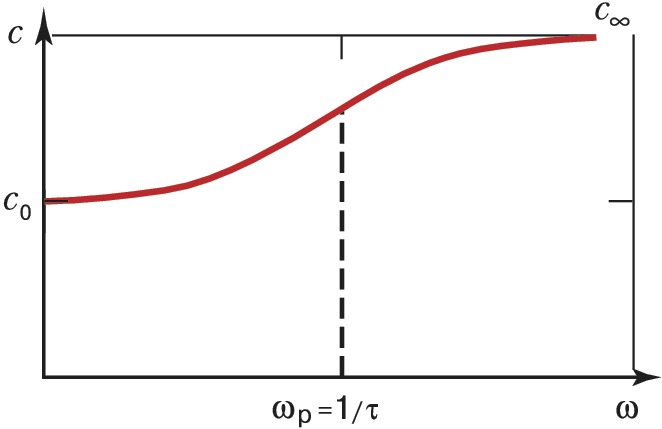
ДИСПЕ́РСИЯ ЗВУ́КА, за­ви­си­мость фа­зо­вой ско­ро­сти гар­мо­нич. аку­стических (зву­ко­вых) волн от час­то­ты. Раз­ли­ча­ют Д. з., обу­слов­лен­ную фи­зич. свой­ст­ва­ми сре­ды, – фи­зич. дис­пер­сию, и Д. з., обу­слов­лен­ную гра­ни­ца­ми те­ла, в ко­то­ром рас­про­стра­ня­ет­ся вол­на, – гео­мет­рич. дис­пер­сию. Фи­зич. дис­пер­сия воз­ни­ка­ет, ко­гда воз­дей­ст­вие аку­стич. вол­ны при­во­дит к не­рав­но­вес­но­му со­стоя­нию сре­ды, воз­бу­ж­дая в ней внутр. сте­пе­ни сво­бо­ды – ко­ле­ба­тель­ные и вра­ща­тель­ные дви­же­ния мо­ле­кул, ио­ни­за­цию и дис­со­циа­цию мо­ле­кул, хи­мич. ре­ак­ции, пе­ре­строй­ку струк­ту­ры жид­ко­сти и т. п. Вы­рав­ни­ва­ние энер­гии ме­ж­ду по­сту­па­тель­ны­ми и внутр. сте­пе­ня­ми сво­бо­ды про­ис­хо­дит за не­ко­то­рое вре­мя, на­зы­вае­мое вре­ме­нем ре­лак­са­ции $τ$ (см. Ре­лак­са­ция аку­сти­че­ская). Ес­ли пе­ри­од $T$ аку­стич. вол­ны мал по срав­не­нию с τ (вы­со­кие час­то­ты), то за вре­мя $T≪τ$ внутр. сте­пе­ни сво­бо­ды не ус­пе­ва­ют воз­бу­дить­ся. Сре­да ве­дёт се­бя так, как буд­то внутр. сте­пе­ни сво­бо­ды от­сут­ст­ву­ют. Ес­ли же $T≫τ$ (низ­кие час­то­ты), то часть энер­гии по­сту­па­тель­но­го дви­же­ния ус­пе­ет пе­ре­рас­пре­де­лить­ся на внутр. сте­пе­ни сво­бо­ды. При этом вслед­ст­вие умень­ше­ния энер­гии по­сту­па­тель­но­го дви­же­ния уп­ру­гость сре­ды и ско­рость зву­ка бу­дут мень­ше, чем в слу­чае вы­со­ких час­тот. Т. о., при на­ли­чии фи­зич. дис­пер­сии ско­рость зву­ка уве­ли­чи­ва­ет­ся с рос­том час­то­ты (рис.).

Ско­рость зву­ка рас­тёт бы­ст­рее все­го при час­то­тах, близ­ких к час­то­те ре­лак­са­ции $ω_р=1/τ$. Для боль­шин­ст­ва сред час­то­та $ω_р$ ле­жит в об­лас­ти 104–1010 Гц. Ве­ли­чи­на Д. з., оп­ре­де­ляе­мая как $Δ=(c_∞-c_0)/c_0$ ($c_0$ – ско­рость зву­ка на час­то­тах мно­го мень­ших час­то­ты ре­лак­са­ции, $c_∞$ – ско­рость зву­ка на час­то­тах мно­го боль­ших час­то­ты ре­лак­са­ции), мо­жет силь­но раз­ли­чать­ся для раз­ных ве­ществ – от до­лей про­цен­та в мор. во­де до де­сят­ков про­цен­тов в силь­но­вяз­ких и вы­со­ко­мо­ле­ку­ляр­ных со­еди­не­ни­ях. Д. з. мо­жет про­яв­лять­ся так­же в сре­де с вкра­п­лён­ны­ми не­од­но­род­но­стя­ми, ес­ли энер­гия по­сту­па­тель­но­го дви­же­ния мо­жет пе­ре­да­вать­ся вкра­п­ле­ни­ям. Д. з. со­про­во­ж­да­ет­ся по­гло­ще­ни­ем зву­ка, при­чём наи­боль­шее по­гло­ще­ние при­хо­дит­ся на об­ласть час­тот вбли­зи час­то­ты ре­лак­са­ции.

Про­стей­шим при­ме­ром гео­мет­рич. Д. з. яв­ля­ет­ся дис­пер­сия при рас­про­стра­не­нии из­гиб­ных волн в стерж­нях и пла­сти­нах. Ко­эф. уп­ру­го­сти при из­гиб­ной де­фор­ма­ции рас­тёт с умень­ше­ни­ем дли­ны из­ги­бае­мо­го уча­ст­ка, ко­то­рый в дан­ном слу­чае оп­ре­де­ля­ет­ся дли­ной из­гиб­ной вол­ны. Вслед­ст­вие это­го эф­фек­тив­ная уп­ру­гость, а вме­сте с ней и ско­рость вол­ны рас­тут при умень­ше­нии дли­ны вол­ны, т. е. при уве­ли­че­нии час­то­ты. Ско­рость из­гиб­ной вол­ны про­пор­цио­наль­на квад­рат­но­му корню из час­то­ты.

Гео­мет­рич. Д. з. на­блю­да­ет­ся так­же при рас­про­стра­не­нии нор­маль­ных волн в аку­сти­че­ских вол­но­во­дах. Напр., в вол­но­во­де с жё­ст­ки­ми стен­ка­ми фа­зо­вые ско­ро­сти нор­маль­ных волн оп­ре­де­ля­ют­ся со­от­но­ше­ния­ми $$c_n=\frac{c}{\sqrt{1-(n\pi c/\omega h)^2}},$$  

где $n=1, 2, 3, ...$ – но­мер нор­маль­ной вол­ны, $c$ – ско­рость зву­ка в сво­бод­ном про­стран­ст­ве, $h$ – ши­ри­на вол­но­во­да. Фа­зо­вая ско­рость нор­маль­ной вол­ны боль­ше ско­ро­сти зву­ка в сво­бод­ном про­стран­ст­ве и умень­ша­ет­ся с рос­том час­тоты.

Д. з. обо­их ти­пов при­во­дит к рас­плы­ва­нию фор­мы зву­ко­во­го им­пуль­са при его рас­про­стра­не­нии. Это осо­бен­но важ­но в гид­ро­аку­сти­ке, ат­мо­сфер­ной аку­сти­ке и гео­аку­сти­ке, где име­ют де­ло с рас­про­стра­не­ни­ем зву­ка на боль­шие рас­стоя­ния, в не­ли­ней­ной аку­сти­ке, ко­гда на­ли­чие Д. з. мо­жет при­вес­ти к умень­ше­нию по­гло­ще­ния зву­ка, а так­же при при­ме­не­нии аку­стич. волн в из­ме­ри­тель­ной тех­ни­ке.