АМПЕ́РА ЗАКО́Н

АМПЕ́РА ЗАКО́Н, за­кон ме­ха­ни­че­ско­го (пон­де­ро­мо­тор­но­го) взаи­мо­дей­ст­вия двух элек­трич. то­ков, те­ку­щих в ма­лых от­рез­ках про­вод­ни­ков, на­хо­дя­щих­ся на не­ко­то­ром рас­стоя­нии друг от дру­га. Ус­та­нов­лен А. М. Ам­пе­ром в 1820.

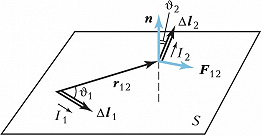
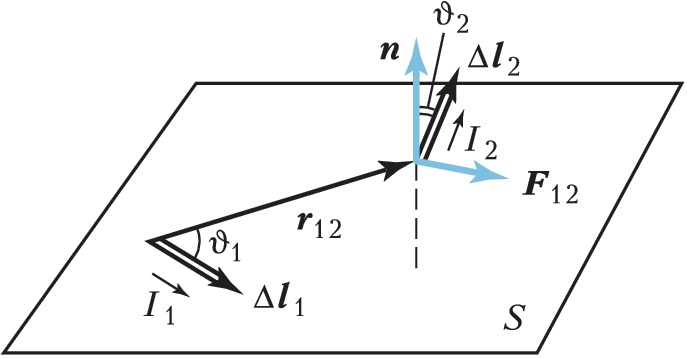
Со­глас­но А. з., си­ла $F_{12}$, дей­ст­вую­щая со сто­ро­ны пер­во­го от­рез­ка про­вод­ни­ка $\Delta l_1$ на от­ре­зок $\Delta l_2$ (рис.), рав­на:$$F_{12}=k\frac{I_1I_2\Delta I_1\Delta I_2 \sinϑ_1\sinϑ_2}{r^2_{12}}(1)$$

Ра­ди­ус-век­тор $\boldsymbol r_{12}$ счи­та­ет­ся на­прав­лен­ным от $\Delta l_1$ к $\Delta l_2$, от­рез­кам при­пи­сы­ва­ют­ся на­прав­ле­ния те­ку­щих в них то­ков $I_1$ и $I_2$; $ϑ_1$ – угол ме­ж­ду век­то­ра­ми $\Delta \boldsymbol l_1$ и $\boldsymbol r_{12}$; $ϑ_2$ – угол ме­ж­ду век­то­ром $\Delta \boldsymbol l_2$ и пер­пен­ди­ку­ля­ром $\boldsymbol n$ к плос­ко­сти $S$, содер­жа­щей $\Delta \boldsymbol l_1$ и $\boldsymbol r_{12}$ (на­прав­ле­ние $n$ совпа­да­ет с по­сту­па­тель­ным дви­же­ни­ем пра­во­го бу­рав­чи­ка при вра­ще­нии его ру­ко­ят­ки в плос­ко­сти $S$ от $\Delta l_1$ к $r_{12}$); $k$ – ко­эф., за­ви­ся­щий от вы­бо­ра сис­темы еди­ниц (в сис­те­ме еди­ниц Га­ус­са $k=1/c^2$, где $c$ – ско­рость све­та в ва­куу­ме, в СИ $k=μ_0/4\pi$, где $μ_0=4\pi·10^{–7}$ Гн/м – маг­нит­ная про­ни­цае­мость ва­куу­ма).

Си­ла взаи­мо­дей­ст­вия двух про­вод­ни­ков с то­ка­ми (эле­мен­тов то­ка) не яв­ля­ет­ся цен­траль­ной: на­прав­ле­ние $\boldsymbol F_{12}$ не сов­па­да­ет с пря­мой, со­еди­няю­щей от­рез­ки. Эта си­ла пер­пен­ди­ку­ляр­на $\Delta \boldsymbol l_2$ и ле­жит в плос­ко­сти $S$. На­прав­ле­ние си­лы оп­ре­де­ля­ет­ся пра­ви­лом бу­рав­чи­ка: при вра­ще­нии ру­ко­ят­ки бу­рав­чи­ка от $\Delta \boldsymbol l_2$ к $\boldsymbol n$ по­сту­па­тель­ное дви­же­ние бу­рав­чи­ка ука­зы­ва­ет на­прав­ле­ние $\boldsymbol F_{12}$.

Си­ла $F_{21}$, с ко­то­рой вто­рой эле­мент то­ка дей­ст­ву­ет на пер­вый, вы­ра­жа­ет­ся фор­му­лой, ана­ло­гич­ной (1). В об­щем слу­чае про­из­воль­но ори­ен­ти­ро­ван­ных век­то­ров $\Delta \boldsymbol l_1$ и $\Delta \boldsymbol l_2$ век­то­ры $\boldsymbol F_{12}$ и $\boldsymbol F_{21}$ не ле­жат на од­ной пря­мой и не удов­ле­тво­ря­ют прин­ци­пу ра­вен­ст­ва дей­ст­вия и про­ти­во­дей­ст­вия. В слу­чае па­рал­лель­ных про­вод­ни­ков си­лы взаи­мо­дей­ст­вия стре­мят­ся сбли­зить про­вод­ни­ки, ес­ли то­ки те­кут в них в од­ном на­прав­ле­нии, и уда­лить их друг от дру­га, ес­ли то­ки те­кут в про­ти­во­по­лож­ных на­прав­ле­ни­ях.

А. з. на­зы­ва­ют так­же фор­му­лу, оп­ре­де­ляю­щую си­лу $\mathbf{\mathit F}$, с ко­то­рой маг­нит­ное по­ле, ха­рак­те­ри­зуе­мое век­то­ром маг­нит­ной ин­дук­ции $\boldsymbol B$, дей­ст­ву­ет на эле­мен­тар­ный от­ре­зок про­вод­ни­ка $\Delta l$, по ко­то­ро­му те­чёт элек­трич. ток си­лой $I$:$$F=kI\Delta lB\sin ϑ, (2)$$где $ϑ$ – угол ме­ж­ду на­прав­ле­ния­ми $\Delta \boldsymbol l$ и $\boldsymbol B$. В сис­те­ме еди­ниц Га­ус­са $k=1/c$, в СИ $k=1$. Фор­му­ла (2) по­лу­ча­ет­ся из фор­му­лы (1), ес­ли в ней вы­де­лить часть, не со­дер­жа­щую ве­ли­чин, от­но­ся­щих­ся ко вто­ро­му эле­мен­ту то­ка, и под $\boldsymbol B$ по­ни­мать маг­нит­ную ин­дук­цию, соз­да­вае­мую пер­вым эле­мен­том в точ­ке, где рас­по­ло­жен вто­рой эле­мент то­ка (см. Био–Са­ва­ра за­кон).