СФЕРИ́ЧЕСКАЯ СИСТЕ́МА КООРДИНА́Т

СФЕРИ́ЧЕСКАЯ СИСТЕ́МА КООРДИ­НА́Т, сис­те­ма ко­ор­ди­нат в про­стран­ст­ве, в ко­то­рой ко­ор­ди­на­та­ми точ­ки яв­ля­ют­ся чис­ла $r$, $θ$, $φ$, свя­зан­ные с пря­мо­уголь­ны­ми ко­ор­ди­на­та­ми $x$, $y$, $z$ фор­му­ла­ми $$x=r\cos φ \sin θ,\\ y=r \sin φ \sin θ,\\ z=r \cos θ,$$

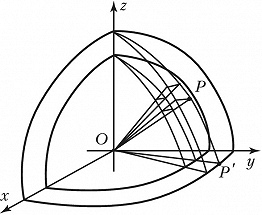
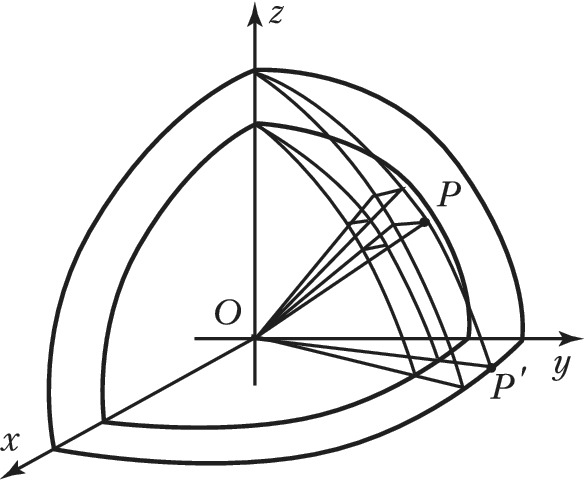
где $0 ⩽ r < ∞$, $0 ⩽ φ < 2π$, $0 ⩽ θ ⩽ π$. Ко­ор­ди­нат­ные по­верх­но­сти (рис.): кон­цен­трич. сфе­ры с цен­тром $O$ ($r=OP= \text{const}$); по­лу­плос­ко­сти, про­хо­дя­щие че­рез ось $Oz$ ($φ=\angle zOP'=\text{const}$); кру­го­вые ко­ну­сы с вер­ши­ной $O$ и осью $Oz$ ($θ=\angle xOP=\text{const}$). Эле­мент пло­ща­ди $$ds=\{ r^2\sin^2 θ(drdφ)^2 + r^2(drdθ)^2 + r^4\sin^2 θ (dφdθ)^2\}^{1/2}.$$ Эле­мент объ­ё­ма $$dV=r^2sinθdrdφdθ.$$ Опе­ра­тор Ла­п­ла­са $$Δf = \frac{\partial^2 f}{\partial r^2} + \frac{2}{r} \frac{2\partial f}{\partial r} + \\ + \frac{1}{r^2\sin^2 θ} \frac{\partial^2 f}{\partial φ^2} + \frac{1}{r^2} \frac{\partial^2 f}{\partial θ^2} + \frac{\text{ctg}\, θ}{r^2} \frac{\partial f}{\partial θ}.$$

C. с. к. из­дав­на упот­реб­ля­лись в ас­тро­но­мии; фор­му­лы, свя­зы­ваю­щие С. с. к. с пря­мо­уголь­ны­ми ко­ор­ди­на­та­ми, по­луче­ны Ж. Ла­гран­жем (1773), на­зва­ние «С. с. к.» пред­ло­жил нем. ма­те­ма­тик Г. Р. Бальт­цер (Баль­цер).