РИ́МАНА СФЕ́РА

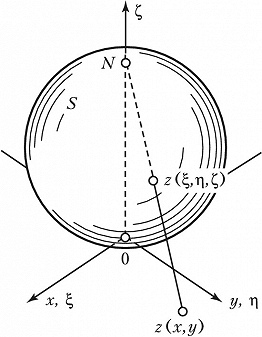
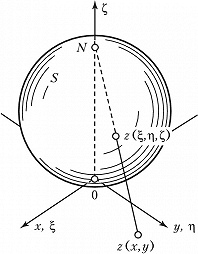
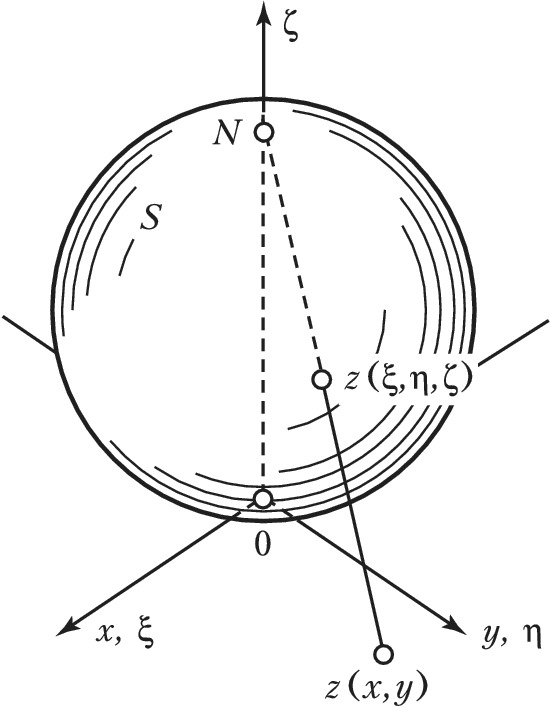
РИ́МАНА СФЕ́РА (ри­ма­но­ва сфе­ра), од­но из воз­мож­ных гео­мет­рич. изо­бра­же­ний со­во­куп­но­сти ком­плекс­ных чи­сел, пред­ло­жен­ное Б. Ри­ма­ном

в 1851. Ком­плекс­ные чис­ла $$z=x+iy=r(\cos j+i\sin j),$$ где $i$ – мни­мая еди­ни­ца, мож­но изо­бра­жать точ­ка­ми ком­плекс­ной плос­ко­сти с де­кар­то­вы­ми $x$, $y$ или по­ляр­ны­ми $r$, $φ$ ко­ор­ди­на­та­ми. В ка­че­ст­ве Р. с. мож­но при­нять сфе­ру ра­диу­са 1, ка­саю­щую­ся ком­плекс­ной плос­ко­сти в на­ча­ле ко­ор­ди­нат, и ка­ж­дое ком­плекс­ное чис­ло $z$ изо­бра­зить на Р. с. точ­кой пе­ре­се­че­ния от­рез­ка $Nz$, со­еди­няю­ще­го эту точ­ку с сев. по­лю­сом Р. с. (рис.). Та­кое ото­бра­же­ние на­зы­ва­ет­ся сте­рео­гра­фич. про­ек­ци­ей. Чис­ло 0 изо­бра­жа­ет­ся юж. по­лю­сом Р. с.; чис­ла с оди­на­ко­вым ар­гу­мен­том $φ=\text{const}$ (лу­чи в ком­плекс­ной плос­ко­сти) изо­бра­жа­ют­ся на Р. с. ме­ри­диа­на­ми, а чис­ла с оди­на­ко­вым мо­ду­лем $|z|=r= =\text{const}$ (ок­руж­но­сти с цен­тром в на­ча­ле ко­ор­ди­нат в ком­плекс­ной плос­ко­сти) – па­рал­ле­ля­ми Р. с. Сев. по­лю­су $N$ Р. с. не со­от­вет­ст­ву­ет ни­ка­кое ком­плекс­ное чис­ло. Од­на­ко в не­ко­то­рых за­да­чах бы­ва­ет удоб­но до­пол­нить ком­плекс­ную плос­кость бес­ко­неч­но уда­лён­ной точ­кой $z=∞$, в этом слу­чае мож­но счи­тать, что она со­от­вет­ст­ву­ет сев. по­лю­су Ри­ма­на сфе­ры.