ПОГО́НИ ЛИ́НИЯ

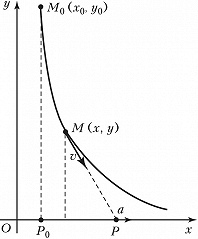
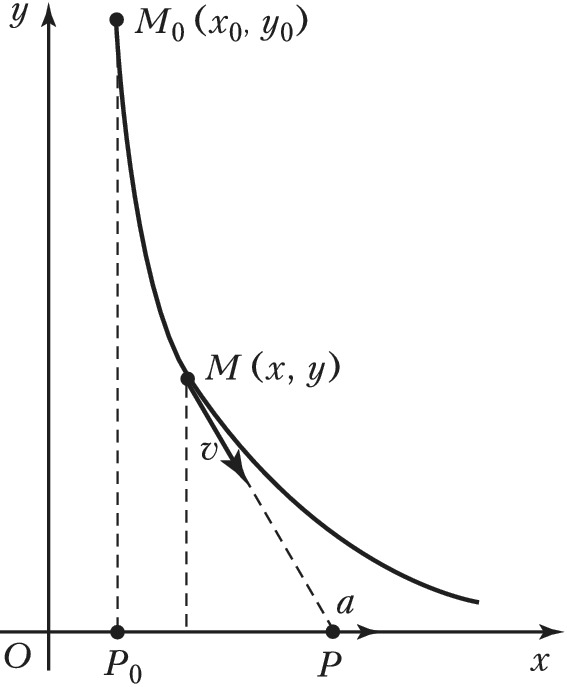
ПОГО́НИ ЛИ́НИЯ, кри­вая, яв­ляю­щая­ся ре­ше­ни­ем за­да­чи о по­го­не, ко­то­рая ста­вит­ся сле­дую­щим об­ра­зом. По пря­мой $Ox$ с по­сто­ян­ной ско­ро­стью $a\gt 0$ дви­жет­ся точ­ка $P$; в плос­ко­сти $Oxy$ дви­жет­ся точ­ка $M(x,y)$ с по­сто­ян­ной по мо­ду­лю ско­ро­стью так, что век­тор ско­ро­сти точ­ки $M$ все­гда на­прав­лен в точ­ку $P$; тра­ек­то­рия точ­ки $M$ на­зы­ва­ет­ся ли­ни­ей по­го­ни (рис.). Диф­фе­рен­ци­аль­ное урав­не­ние П. л. име­ет вид $$y''=\frac{a}{v}\frac{y'^2}{y}\sqrt{1+y'^2},$$где $v$ – мо­дуль ско­ро­сти точ­ки $M$. Ре­шение это­го урав­не­ния да­ёт сле­дую­щую связь ме­ж­ду ко­ор­ди­на­та­ми то­чек П. л. $$x=\frac{y_0}{2(1+a/v)}\left[ \left( \frac{y}{y_0} \right)^{1+a/v} - 1\right] - \frac{y_0}{2(1-a/v)}\left[ \left( \frac{y}{y_0} \right)^{1-a/v} - 1\right]+x_0$$ при $v≠a$ и $$x=\frac{y_0}{4}\left[ \left( \frac{y}{y_0} \right)^2 - 1 \right] - \frac{y_0}{2}\ln \frac{y}{y_0}+x_0$$ при $v=a$, где $x_0,y_0$ – ко­ор­ди­на­ты точ­ки  $M$ в на­чаль­ный мо­мент вре­ме­ни, а точ­ка $P$ име­ет в этот мо­мент ко­ор­ди­на­ты $x_0,0$. Ес­ли $v\gt a$, то $y$ убы­ва­ет от $y_0$ до $0$, ко­гда $x$ воз­рас­та­ет от $x_0$ до $x_1=x_0+y_0 \frac{av}{v^2-a^2}$, т. е. точ­ка $M$ до­го­ня­ет точ­ку $P$ при $x=x_1$. В этом слу­чае дли­на П. л. рав­на $y_0v^2/(v^2-a^2)$ и точ­ка $M$ до­го­ня­ет точ­ку $P$ за вре­мя $T=y_0v/(v^2-a^2)$ (про­дол­жи­тель­ность по­го­ни). При $v\leqslant a$ точ­ка $M$ не до­го­ня­ет точку $P$. Из­вест­но обоб­ще­ние за­да­чи о по­го­не на слу­чай, ко­гда точ­ка $P$ дви­жет­ся по кри­вой ли­нии.

За­да­ча о П. л. бы­ла по­став­ле­на Ле­о­нар­до да Вин­чи, ре­ше­на П. Бу­ге­ром (1732).