ОСО́БОЕ РЕШЕ́НИЕ

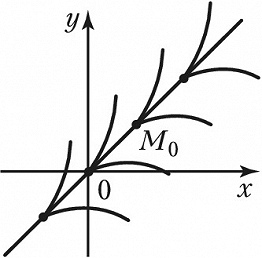
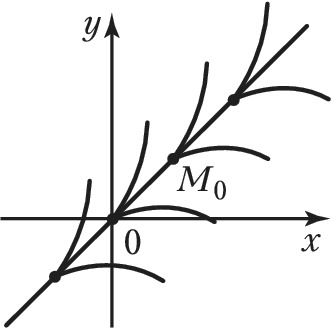
ОСО́БОЕ РЕШЕ́НИЕ диф­фе­рен­ци­аль­но­го урав­не­ния, ре­ше­ние, в ка­ж­дой точ­ке ко­то­ро­го на­ру­ша­ет­ся един­ст­вен­ность. Для урав­не­ния $y'=f(x,y)$ это оз­на­ча­ет, что че­рез ка­ж­дую точ­ку О. р. про­хо­дит неск. разл. ин­те­граль­ных кри­вых (имею­щих в этой точ­ке об­щую ка­са­тель­ную). При не­пре­рыв­но­сти $f(x,y)$ по­след­нее воз­мож­но, лишь ес­ли в точ­ках О. р. для функ­ции $f(x,y)$ не вы­пол­не­но Лип­ши­ца ус­ло­вие

по $y$. Напр., для урав­не­ния $y'=1+\sqrt[3]{y-x}$ О. р. (рис.) яв­ля­ет­ся пря­мая $y=x$: че­рез лю­бую точ­ку $M_0(x_0,y_0)$ этой пря­мой, кро­ме са­мой пря­мой, про­хо­дят ин­те­граль­ные кри­вые $$y=x \pm \left(\frac{2}{3}(x-x_0)\right)^{3/2}.$$ Гео­мет­ри­че­ски О. р. пред­став­ля­ет со­бой оги­баю­щую се­мей­ст­ва ин­те­граль­ных кри­вых $Ф(x,y,c)=0$, об­ра­зую­щих об­щий ин­те­грал урав­не­ния.

Для диф­фе­рен­ци­аль­но­го урав­не­ния $F(x,y,y')=0$ оп­ре­де­ля­ет­ся дис­кри­ми­нант­ная кри­вая $D(x,y)=0$ как ре­зуль­тат ис­клю­че­ния па­ра­мет­ра $p=y'$ из сис­те­мы $F(x,y,p)=0$, $F'_p(x,y,p)=0$. О. р. яв­ля­ет­ся, во­об­ще го­во­ря, лишь ча­стью этой кри­вой.