ГИПЕ́РБОЛА

Рис. 1.

Рис. 2.

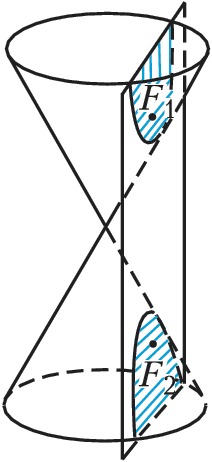
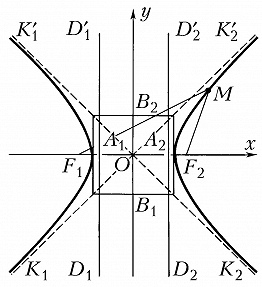
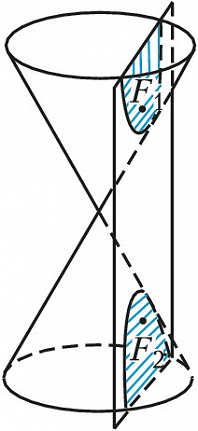
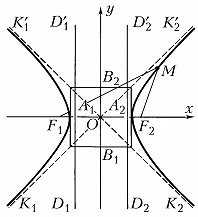
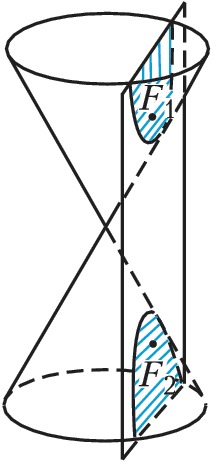
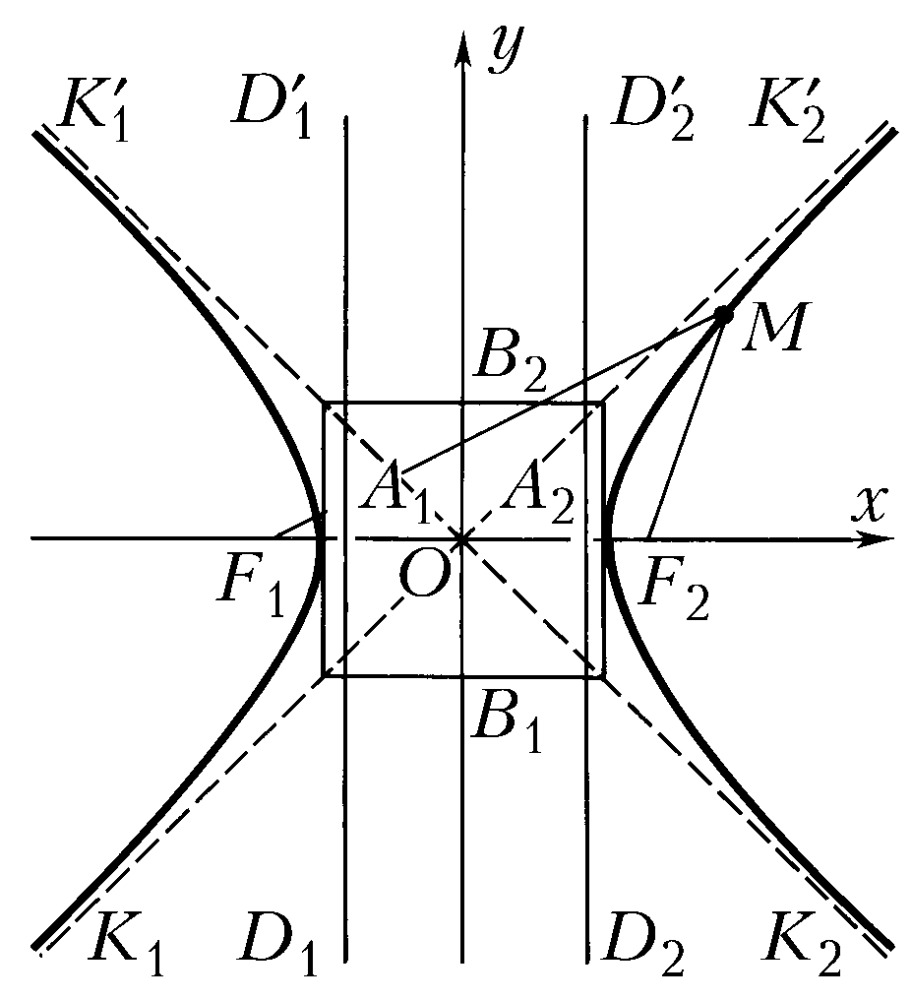
ГИПЕ́РБОЛА, ли­ния пе­ре­се­че­ния пря­мо­го кру­го­во­го ко­ну­са плос­ко­стью, не про­хо­дя­щей че­рез вер­ши­ну ко­ну­са и пе­ре­се­каю­щей обе его по­лос­ти (рис. 1). Г. мо­жет быть так­же оп­ре­де­ле­на как гео­мет­рич. ме­сто то­чек $M$ плос­ко­сти, раз­ность рас­стоя­ний ко­то­рых до двух оп­ре­де­лён­ных то­чек $F_1$ и $F_2$ плос­ко­сти (фо­ку­сов Г.) по­сто­ян­на. Ес­ли вы­брать сис­те­му ко­ор­ди­нат $xOy$ так, как ука­за­но на рис. 2 ($OF_1=OF_2=c$), то урав­не­ние Г. при­мет вид:$$\frac {x^2}{a^2} - \frac {y^2}{b^2}=1,$$где $2a=F_1M-F_2M$, $b= \sqrt {c^2-a^2}$. Г. – ли­ния вто­ро­го по­ряд­ка, со­сто­ит из двух бес­ко­неч­ных вет­вей $K_1A_1K'_1$ и $K_2A_2K'_2$, она сим­мет­рич­на от­но­си­тель­но осей $F_1F_2$ и $B_1B_2$, точ­ка $O$ (центр Г.) яв­ля­ет­ся её цен­тром сим­мет­рии, от­рез­ки $A_1A_2=2a, B_1B_2=2b$ на­зы­ва­ют­ся со­от­вет­ст­вен­но дей­ст­ви­тель­ной осью Г. и мни­мой осью Г., чис­ло $e=c/a>1$ – экс­цен­три­сите­том Г. Пря­мые $D_1D'_1$ и $D_2D'_2$, урав­не­ния ко­то­рых суть $x=–a/e$ и $x=a/e$, на­зы­ва­ют ди­рек­три­са­ми Г., от­но­ше­ние рас­стоя­ния точ­ки Г. до бли­жай­ше­го фо­ку­са к рас­стоя­нию до бли­жай­шей ди­рек­три­сы по­сто­ян­но и рав­но экс­цен­т­ри­сите­ту. Точ­ки $A_1$ и $A_2$ пе­ре­се­че­ния Г. с осью Ox на­зы­ва­ют­ся её вер­ши­на­ми. Пря­мые $y=±bx/a$ (изо­бра­жён­ные на рис. 2 пунк­ти­ром) – асим­пто­ты Г. Гра­фик об­рат­но про­пор­цио­наль­ной за­ви­си­мо­сти $y=k/x$ яв­ля­ет­ся Г. См. так­же Ко­ни­че­ские се­че­ния.