ВЫ́ПУКЛОСТЬ И ВО́ГНУТОСТЬ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
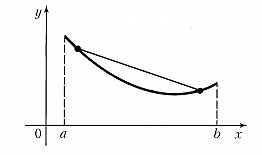
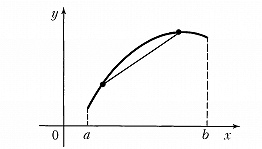
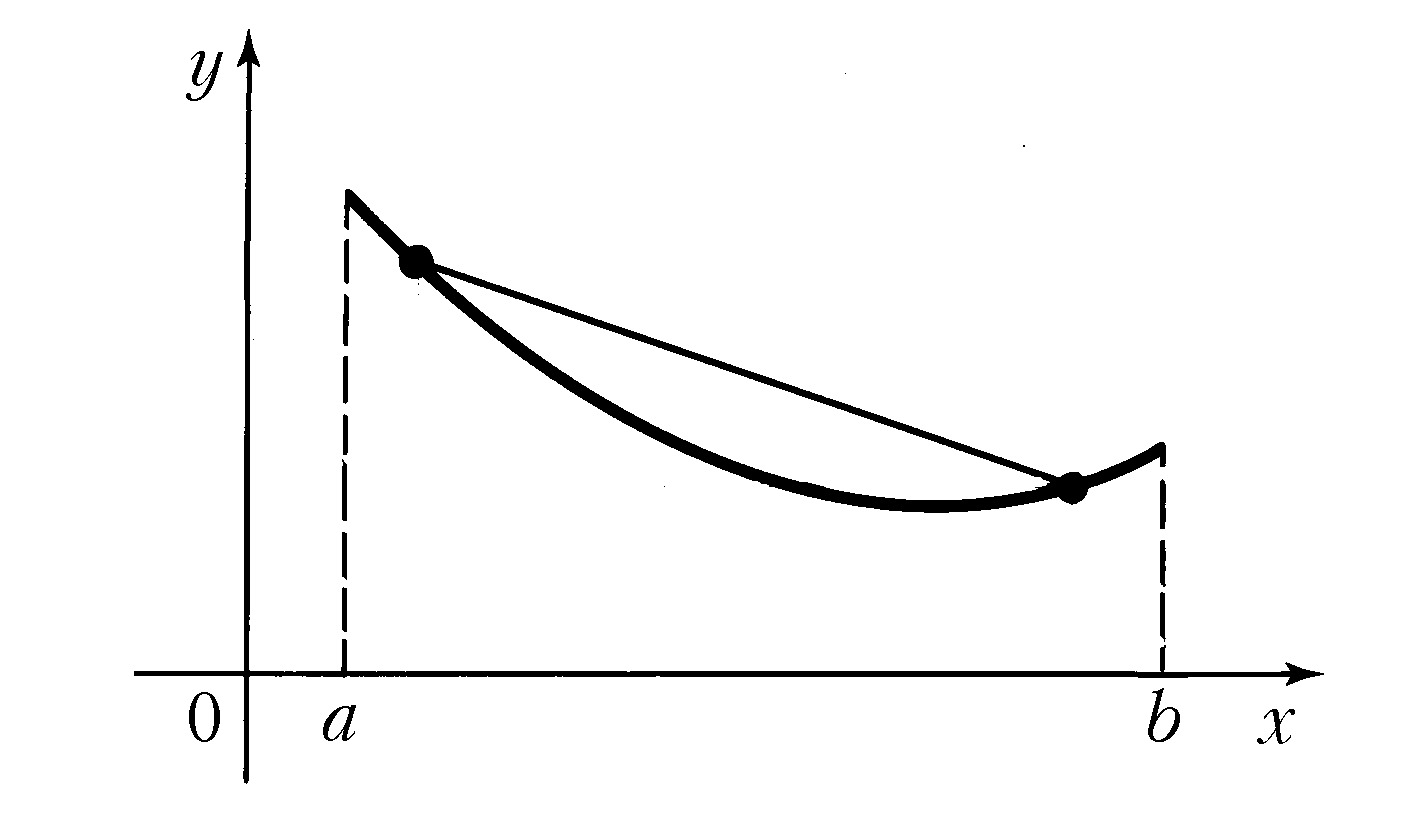
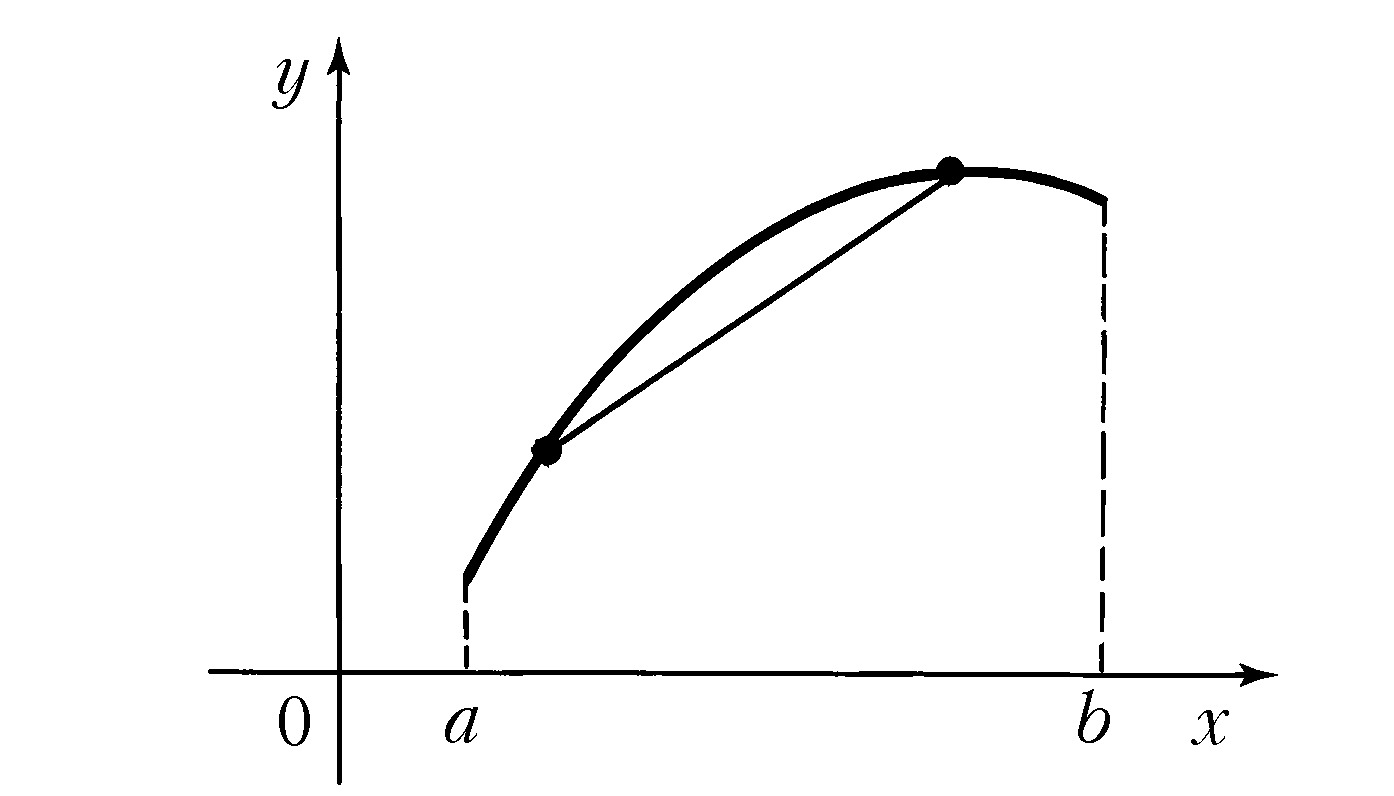
ВЫ́ПУКЛОСТЬ И ВО́ГНУТОСТЬ функции, свойство функции $f(x)$, определённой на некотором промежутке, заключающееся в том, что каждая дуга кривой, являющейся графиком функции $y=f(x)$, лежит не выше или не ниже своей хорды. В случае когда каждая дуга кривой лежит не выше своей хорды, функцию $f $называют выпуклой (рис. 1), а в случае когда каждая дуга кривой лежит не ниже своей хорды, – вогнутой (рис. 2) на соответствующем промежутке. Используют и др. терминологию, когда выпуклые функции называют выпуклыми вниз, а вогнутые функции – выпуклыми вверх.
Если функция $f(x) $выпукла на отрезке [$a, b$] или на интервале ($a, b$), то в каждой точке $x∈(a, b)$ она непрерывна и имеет односторонние производные справа и слева. Каждая из этих производных является возрастающей функцией. Поэтому выпуклая функция имеет производную на интервале ($a, b$) всюду, за исключением, может быть, конечного или счётного множества точек. Если на интервале ($a, b$) функция $f(x)$ имеет вторую производную, то $f(x)$ выпукла тогда и только тогда, когда $f″(x)⩾0$. В каждой точке графика выпуклой функции можно провести опорную прямую, т. е. такую прямую, что все точки графика функции лежат выше или на самой прямой.
Вогнутость функции $f(x)$ равносильна выпуклости функции –$f(x)$.
Рассматривается В. и в. функций многих переменных. Выпуклость дважды дифференцируемой функции в области равносильна постоянству знака её второго дифференциала в этой области.