ИНВЕ́РСИЯ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
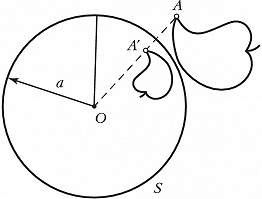
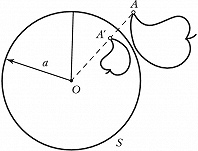
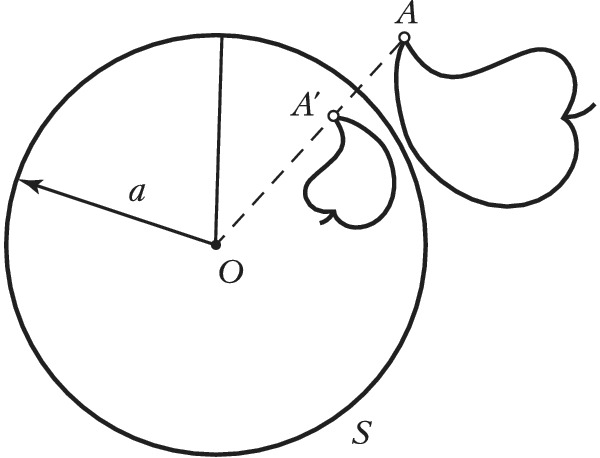
ИНВЕ́РСИЯ в математике, преобразование плоскости, для которого некоторая точка $O$, называемая центром И., фиксирована и любая точка $A$, не совпадающая с $O$, переходит в точку $A′$, лежащую на луче $OA$, такую, что произведение длин отрезков $OA$ и $OA′$ равно некоторому числу $k$, одному и тому же для любой точки $A$ (рис.). Центр И. $O$ иногда называют полюсом И., а $k$ – степенью или коэффициентом И. Точки окружности $S$ с центром $O$ и радиусом переходят при И. сами в себя; образами внешних по отношению к $S$ точек являются внутренние точки, а образами внутренних – внешние; центр И. не имеет образа. Иногда И. называется симметрией относительно окружности. Рассматривается также И. с $k<0$. И. с отрицательным коэф. $k$ равносильна И. с тем же центром $O$ и положит. коэф. $∣k∣$, сопровождаемой симметрией относительно точки $O$. И. с $k>0$ называется гиперболич., а с $k<0$ – эллиптич. И. или антиинверсией.
Прямая, проходящая через центр И., преобразуется в себя. Прямая, не проходящая через центр И., преобразуется в окружность без одной точки. Эта окружность проходит через точку $O$, и точка $O$ исключается из окружности, обратное также верно. Окружности, ортогональные к окружности с центром $O$ и радиусом $\sqrt{∣k∣}$ преобразуются сами в себя. В декартовых прямоугольных координатах И. с центром в начале координат может быть задана формулами $$x'=\frac{kx}{x^2+y^2},\, y'=\frac{ky}{x^2+y^2},$$ или, в плоскости комплексного переменного, формулой $z′ = k/ \bar{z}$ где черта означает комплексное сопряжение.
Аналогично определяется И. относительно сферы в пространстве.
Преобразование И. с 1824 систематически применял швейц. математик Я. Штейнер.