ЖУКО́ВСКОГО ФУ́НКЦИЯ

Рис. 2.

Рис. 1.

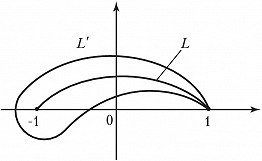
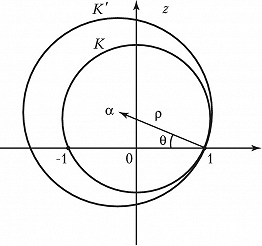
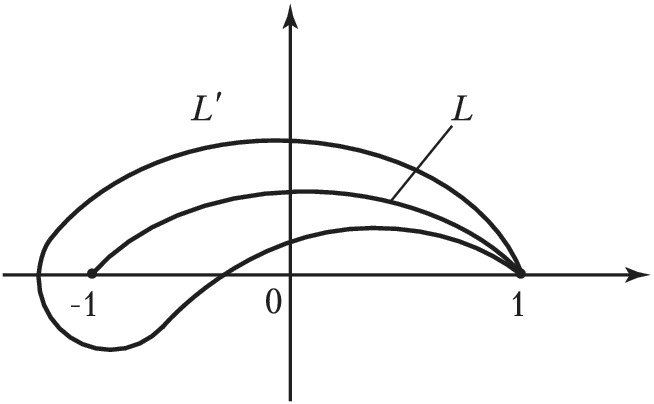
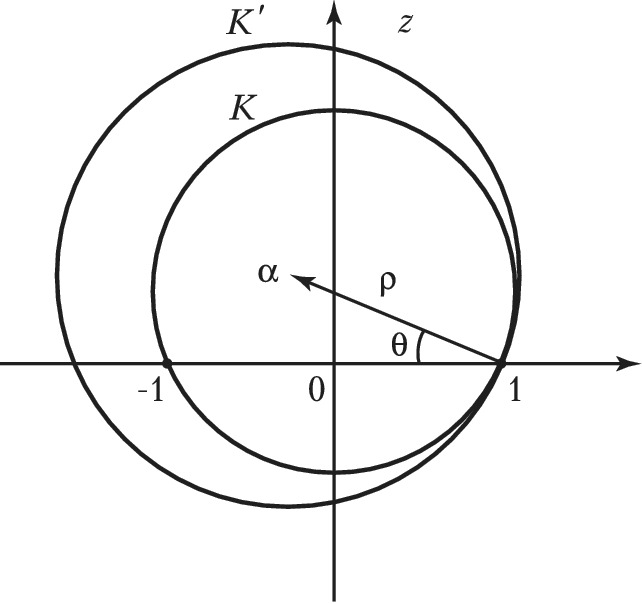
ЖУКО́ВСКОГО ФУ́НКЦИЯ, ра­цио­наль­ная функ­ция $$\lambda (z)=\frac{1}{2}\left (z+\frac {1}{z} \right )$$ком­плекс­но­го пе­ре­мен­но­го $z = x + iy$. Важ­на свои­ми при­ме­не­ния­ми в аэ­ро- и гид­ро­ди­на­ми­ке, от­кры­ты­ми Н. Е. Жу­ков­ским (1911). Осн. при­ме­не­ние Ж. ф. на­хо­дит при по­строе­нии про­фи­лей кры­ла са­мо­лё­та, на­зы­вае­мых про­фи­ля­ми Жу­ков­ско­го. Пусть в плос­ко­сти $z$ за­да­ны ок­руж­ность $K$, про­хо­дя­щая че­рез точ­ки $z = ± 1$, и ок­руж­ность $K′$ с цен­тром $α$ и ра­диу­сом $ρ$, ка­саю­щая­ся $K$ в точ­ке $z = 1$ так, как по­ка­за­но на рис. 1. При ото­бра­же­нии $w = λ(z)$ об­ра­зом ок­руж­но­сти $K′$ яв­ля­ет­ся не­ко­то­рая замк­ну­тая кри­вая $L′$ (про­филь Жу­ков­ско­го) с ост­ри­ём в точ­ке $w = 1$, ка­саю­щая­ся в этой точ­ке ду­ги ок­руж­но­сти $L$ (об­раза $K$) и изо­бра­жён­ная на рис. 2. Для по­лу­че­ния про­фи­лей Жу­ков­ско­го бо­лее об­ще­го ви­да и рас­по­ло­же­ния при­ме­ня­ет­ся обоб­щён­ная Ж. ф.$$w = \frac {z}{2}(a-b)+ \frac{1}{2z}(a+b), \: a>b>0.$$