ДЕЗА́РГА ПРЕДЛОЖЕ́НИЕ

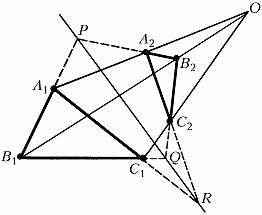
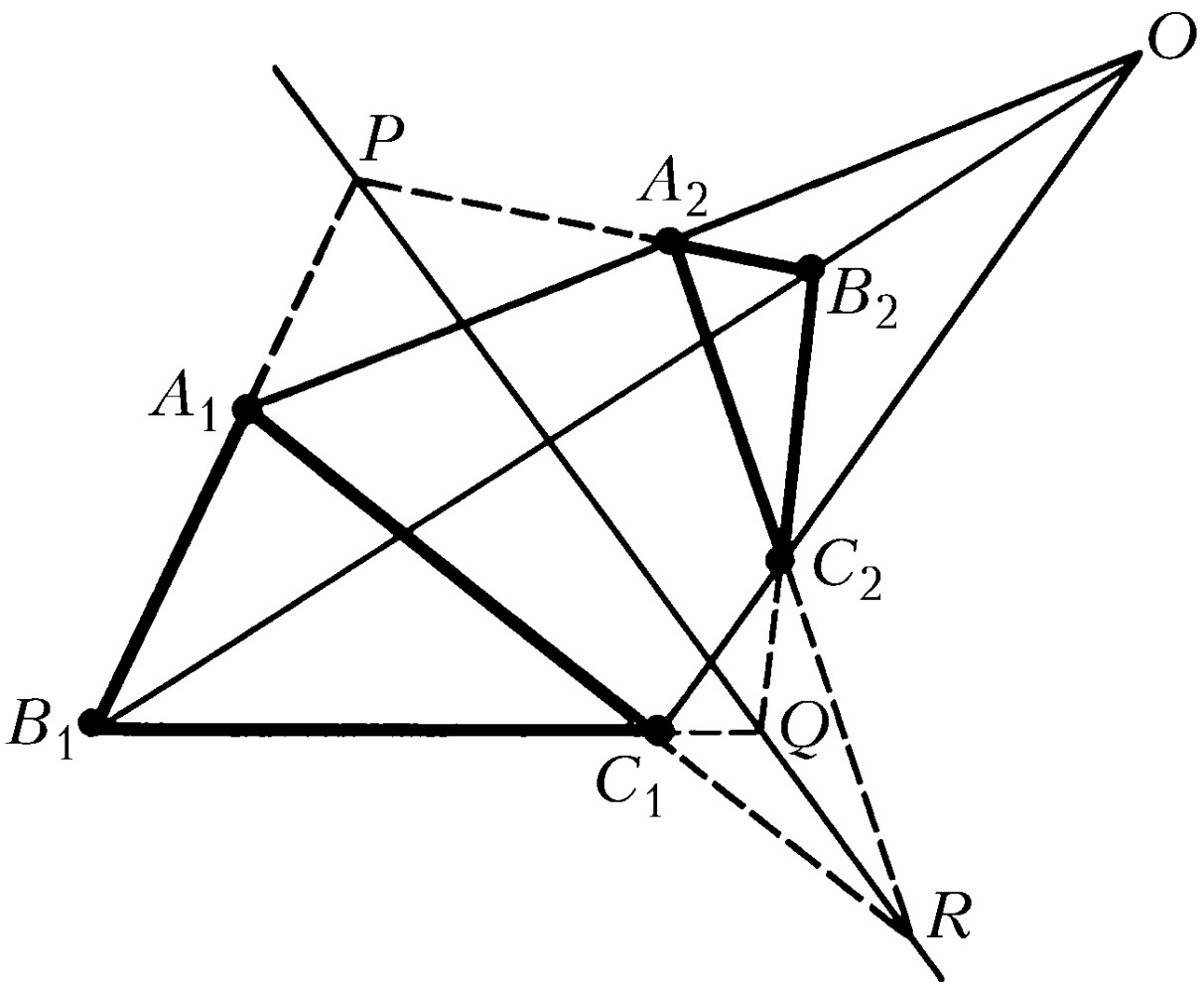
ДЕЗА́РГА ПРЕДЛОЖЕ́НИЕ (тео­ре­ма Де­зар­га), ут­вер­жде­ние, со­стоя­щее в том, что ес­ли со­от­вет­ст­вую­щие сто­ро­ны (или их про­дол­же­ния) двух тре­уголь­ни­ков A₁B₁C₁ и A₂B₂C₂ (рис.) пе­ре­се­ка­ют­ся в точ­ках P, Q, R, ле­жа­щих на од­ной пря­мой, то пря­мые, со­еди­няю­щие со­от­вет­ст­вую­щие вер­ши­ны тре­уголь­ни­ков, пе­ре­се­ка­ют­ся в од­ной точ­ке O. Спра­вед­ли­во и об­рат­ное ут­вер­жде­ние: ес­ли пря­мые, со­еди­няю­щие со­от­вет­ст­вую­щие вер­ши­ны двух тре­уголь­ни­ков, про­хо­дят че­рез точ­ку O, то три точ­ки P, Q, R пе­ре­се­че­ния со­от­вет­ст­вую­щих сто­рон этих тре­уголь­ни­ков ле­жат на од­ной пря­мой. Это ут­вер­жде­ние сфор­му­ли­ро­ва­но Ж. Де­зар­гом (1648). Упо­ми­нае­мые в Д. п. точ­ки и пря­мые мо­гут ока­зать­ся бес­ко­неч­но уда­лён­ны­ми. По­это­му в эле­мен­тар­ной гео­мет­рии, не рас­смат­ри­ваю­щей бес­ко­неч­но уда­лён­ные эле­мен­ты, Д. п. фор­му­ли­ру­ет­ся с не­ко­то­ры­ми из­ме­не­ния­ми. Напр., пер­вая часть Д. п. ви­до­из­ме­ня­ет­ся так: ес­ли точ­ки пе­ре­се­че­ния со­от­вет­ст­вую­щих сто­рон тре­уголь­ни­ков ле­жат на од­ной пря­мой, то пря­мые, со­еди­няю­щие со­от­вет­ст­вую­щие вер­ши­ны, или про­хо­дят че­рез од­ну точ­ку, или па­рал­лель­ны друг дру­гу.

Д. п. иг­ра­ет су­ще­ст­вен­ную роль при по­строе­нии про­ек­тив­ной гео­мет­рии. Со­дер­жа­ние Д. п. от­но­сит­ся к вза­им­но­му рас­по­ло­же­нию пря­мых на плос­ко­сти и не свя­за­но с из­ме­ре­ния­ми. Од­на­ко, как ус­та­но­вил Д. Гиль­берт, Д. п. не мо­жет быть до­ка­за­но в гео­мет­рии на плос­ко­сти без при­вле­че­ния мет­рич. ак­си­ом. При ак­сио­ма­тич. по­строе­нии про­ек­тив­ной гео­мет­рии на плос­ко­сти Д. п. при­ни­ма­ет­ся в ка­че­ст­ве ак­сио­мы, та­кая гео­мет­рия на­зы­ва­ет­ся де­зар­го­вой. Су­ще­ст­ву­ют гео­мет­рии на плос­ко­сти, в ко­то­рых вы­пол­ня­ют­ся все ак­сио­мы про­ек­тив­ной гео­мет­рии, но Д. п. не име­ет в них мес­та; та­кие гео­мет­рии на­зы­ва­ют не­де­зар­го­вы­ми.