НЕЙРО́ННЫЕ СЕ́ТИ

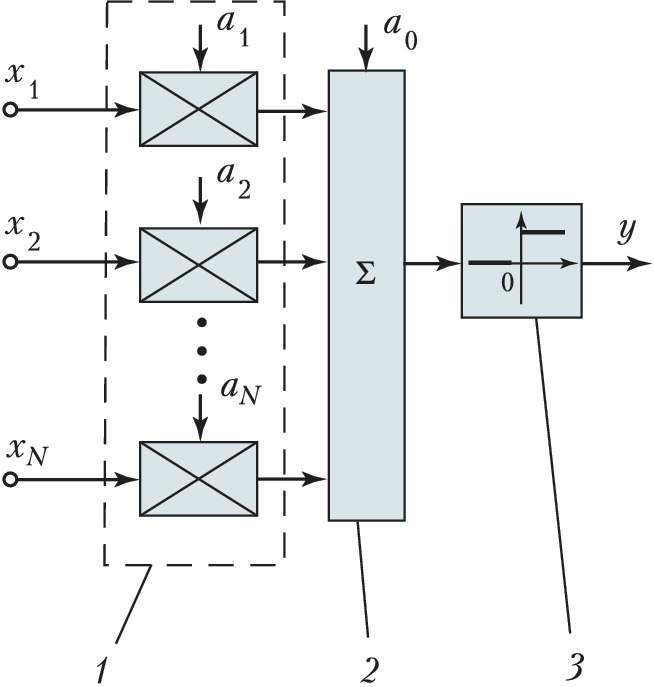
НЕЙРО́ННЫЕ СЕ́ТИ ис­кус­ст­вен­ные, мно­го­слой­ные вы­со­ко­па­рал­лель­ные (т. е. с боль­шим чис­лом не­за­ви­си­мо па­рал­лель­но ра­бо­таю­щих эле­мен­тов) ло­ги­че­ские струк­ту­ры, со­став­лен­ные из фор­маль­ных нейро­нов. По­яв­ле­ние фор­маль­но­го ней­ро­на во мно­гом обу­слов­ле­но изу­че­ни­ем био­ло­гич. ней­ро­нов. Фор­маль­ный ней­рон пред­став­ля­ет со­бой ло­гич. эле­мент с $N$ вхо­да­ми, ($N+1$) ве­со­вы­ми ко­эф­фи­ци­ен­та­ми, сум­ма­то­ром и не­ли­ней­ным пре­об­ра­зо­ва­те­лем. Про­стей­ший фор­маль­ный ней­рон, осу­ще­ст­в­ляю­щий ло­гич. пре­обра­зо­ва­ние $y = \text{sign}\sum_{i=0}^{N}a_ix_i$ вход­ных сигна­лов (ко­то­ры­ми, напр., яв­ля­ют­ся вы­ход­ные сиг­на­лы др. фор­маль­ных ней­ро­нов Н. с.) в вы­ход­ной, пред­став­лен на рис. 1. Здесь $y$ – зна­че­ние вы­хо­да фор­маль­но­го ней­ро­на; $a_i$ – ве­со­вые ко­эф­фи­ци­ен­ты; $x_i$ – вход­ные зна­че­ния фор­маль­но­го ней­ро­на ($x_i∈\left \{0,1\right \},\; x_0=1$). Про­цесс вы­чис­ле­ния вы­ход­но­го зна­че­ния фор­маль­но­го ней­ро­на пред­став­ля­ет со­бой дви­же­ние по­то­ка дан­ных и их пре­об­ра­зо­ва­ние. Сна­ча­ла дан­ные по­сту­па­ют на блок вхо­да фор­маль­но­го ней­ро­на, где про­ис­хо­дит ум­но­же­ние ис­ход­ных дан­ных на со­от­вет­ст­вую­щие ве­со­вые ко­эф­фи­ци­ен­ты. Ве­со­вой ко­эф­фи­ци­ент яв­ля­ет­ся ме­рой, ко­то­рая оп­ре­де­ля­ет, на­сколь­ко со­от­вет­ст­вую­щее вход­ное зна­че­ние влия­ет на со­стоя­ние фор­маль­но­го ней­ро­на. Ве­со­вые ко­эф­фи­ци­ен­ты мо­гут из­ме­нять­ся в со­от­вет­ст­вии с обу­чаю­щи­ми при­мера­ми, ар­хи­тек­ту­рой Н. с., пра­ви­ла­ми обу­че­ния и др. По­лу­чен­ные (при ум­но­же­нии) зна­че­ния пре­об­ра­зу­ют­ся в сум­ма­то­ре в од­но чи­сло­вое зна­че­ние $g$ (по­сред­ст­вом сум­ми­ро­ва­ния). За­тем для оп­ре­де­ле­ния выхо­да фор­маль­но­го ней­ро­на в бло­ке не­ли­ней­но­го пре­об­ра­зо­ва­ния (реа­ли­зую­ще­го пе­ре­да­точ­ную функ­цию) $g$ срав­ни­ва­ет­ся с не­ко­то­рым чис­лом (по­ро­гом). Ес­ли сум­ма боль­ше зна­че­ния по­ро­га, фор­маль­ный ней­рон ге­не­ри­ру­ет сиг­нал, в про­тив­ном слу­чае сиг­нал бу­дет ну­ле­вым или тор­мо­зя­щим. В дан­ном фор­маль­ном ней­ро­не при­ме­ня­ет­ся не­ли­ней­ное пре­об­ра­зо­ва­ние: $$\text{sign}(g)= \begin{cases} 0,\; g < 0, \\ 1,\; g ⩾ 0. \end{cases}$$

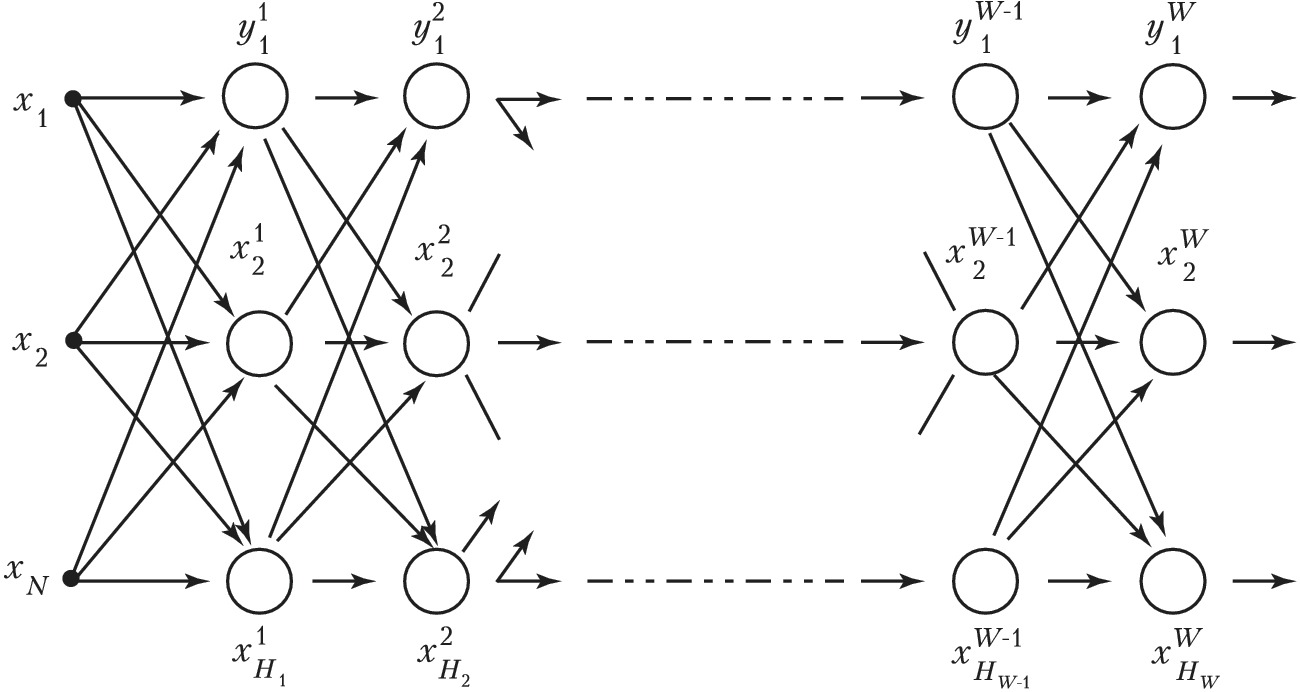
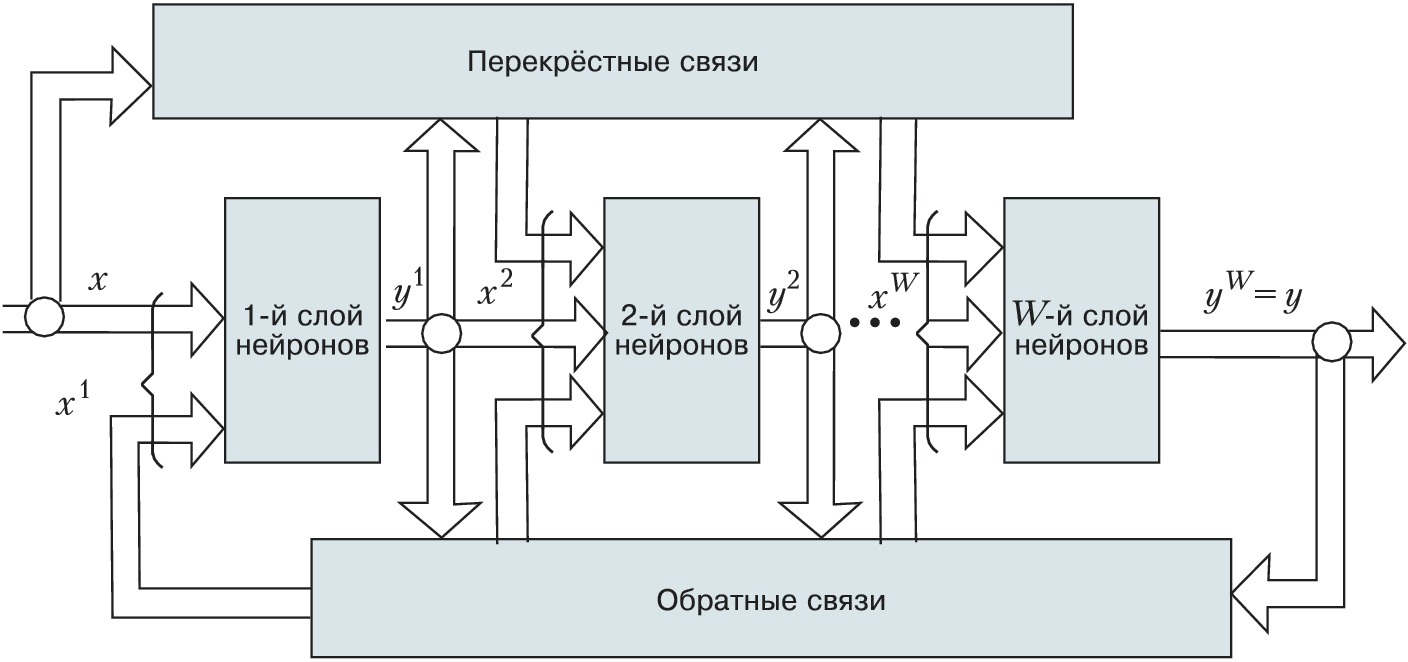
На рис. 2 по­ка­за­на об­щая схе­ма мно­го­слой­ной Н. с. с по­сле­до­ва­тель­ны­ми свя­зя­ми. Вы­со­кий па­рал­ле­лизм об­ра­бот­ки дос­ти­га­ет­ся пу­тём объ­е­ди­не­ния боль­шо­го чис­ла фор­маль­ных ней­ро­нов в слои и со­еди­не­ния оп­ре­де­лён­ным об­ра­зом разл. ней­ро­нов ме­ж­ду со­бой. В об­щем слу­чае в эту струк­ту­ру мо­гут быть вве­де­ны пе­ре­крё­ст­ные и об­рат­ные свя­зи с на­страи­вае­мы­ми ве­со­вы­ми ко­эф­фи­ци­ен­та­ми (рис. 3).

На­ча­ло тео­рии Н. с. по­ло­жи­ла ра­бо­та амер. ней­ро­фи­зио­ло­гов У. Мак-Кал­ло­ка и У. Питт­са «Ло­ги­че­ское ис­чис­ле­ние идей, от­но­ся­щих­ся к нерв­ной дея­тель­но­сти» (1943), в ко­то­рой они пред­ло­жи­ли ма­те­ма­тич. мо­дель био­ло­гич. ней­ро­на. На даль­ней­шее раз­ви­тие тео­рии Н. с. су­ще­ст­вен­ное влия­ние ока­за­ла мо­но­гра­фия амер. ней­ро­фи­зио­ло­га Ф. Ро­зенб­лат­та «Прин­ци­пы ней­ро­ди­на­ми­ки» (1962), в ко­то­рой он под­роб­но опи­сал схе­му пер­цеп­тро­на

(уст­рой­ст­ва, мо­де­ли­рую­ще­го про­цесс вос­при­ятия ин­фор­ма­ции че­ло­ве­че­ским моз­гом). Его идеи по­лу­чи­ли раз­ви­тие в боль­шом чис­ле на­уч. ра­бот др. ав­то­ров. Тео­рия Н. с. про­дол­жа­ет дос­та­точ­но ак­тив­но раз­ви­вать­ся в нач. 21 в.

Н. с. яв­ля­ют­ся слож­ны­ми не­ли­ней­ны­ми сис­те­ма­ми с ог­ром­ным чис­лом сте­пеней сво­бо­ды. Прин­цип, по ко­то­ро­му они об­ра­ба­ты­ва­ют ин­фор­ма­цию, от­ли­ча­ет­ся от прин­ци­па, ис­поль­зуе­мо­го в ком­пь­ю­те­рах на ос­но­ве про­цес­со­ров с фон-ней­ма­нов­ской ар­хи­тек­ту­рой (с ло­гич. ба­зи­сом И, ИЛИ, НЕ). Вме­сто клас­сич. про­грам­ми­ро­ва­ния (как в тра­диц. вы­чис­лит. сис­те­мах) при­ме­ня­ет­ся обу­че­ние Н. с., ко­то­рое сво­дит­ся, как пра­ви­ло, к на­строй­ке ве­со­вых ко­эф­фи­ци­ен­тов с це­лью оп­ти­ми­за­ции за­дан­но­го кри­те­рия ка­че­ст­ва функ­цио­ни­ро­ва­ния Н. с. Ней­ро­се­те­вым ал­го­рит­мом ре­ше­ния за­дач на­зы­ва­ет­ся вы­чис­лит. про­це­ду­ра, осн. часть ко­то­рой или она це­ли­ком реа­ли­зо­ва­на в ви­де Н. с. той или иной струк­ту­ры (напр., мно­го­слой­ная Н. с. с по­сле­до­ва­тель­ны­ми или пе­ре­крё­ст­ны­ми свя­зя­ми ме­ж­ду слоя­ми фор­маль­ных ней­ро­нов) с со­от­вет­ст­вую­щим ал­го­рит­мом на­строй­ки ве­со­вых ко­эф­фи­ци­ен­тов. Ос­но­вой раз­ра­бот­ки ней­ро­се­те­во­го ал­го­рит­ма яв­ля­ет­ся сис­тем­ный под­ход, при ко­то­ром про­цесс ре­ше­ния за­да­чи пред­став­ля­ет­ся как функ­цио­ни­ро­ва­ние во вре­ме­ни не­ко­то­рой ди­на­мич. сис­те­мы. Для её по­строе­ния не­об­хо­ди­мо оп­ре­де­лить: объ­ект, вы­сту­паю­щий в ро­ли вход­но­го сиг­на­ла Н. с.; объ­ект, вы­сту­паю­щий в ро­ли вы­ход­но­го сиг­на­ла Н. с. (напр., не­по­сред­ст­вен­но ре­ше­ние или не­ко­то­рая его ха­рак­те­ри­сти­ка); же­лае­мый (тре­буе­мый) вы­ход­ной сиг­нал Н. с.; струк­ту­ру Н. с. (чис­ло сло­ёв, свя­зи ме­ж­ду слоя­ми, объ­ек­ты, слу­жа­щие ве­со­вы­ми ко­эффи­ци­ен­та­ми); функ­цию ошиб­ки сис­те­мы (ха­рак­те­ри­зую­щую от­кло­не­ние же­лае­мо­го вы­ход­но­го сиг­на­ла Н. с. от ре­аль­но­го вы­ход­но­го сиг­на­ла); кри­те­рий ка­че­ст­ва сис­те­мы и функ­цио­нал её оп­ти­ми­за­ции, за­ви­ся­щий от ошиб­ки; зна­че­ние ве­со­вых ко­эф­фи­ци­ен­тов (напр., оп­ре­де­ляе­мых ана­ли­ти­че­ски не­по­сред­ст­вен­но из по­ста­нов­ки за­да­чи, с по­мо­щью не­ко­то­рых чис­лен­ных ме­то­дов или про­це­ду­ры на­строй­ки ве­со­вых ко­эф­фи­ци­ен­тов Н. с.).

Ко­ли­че­ст­во и тип фор­маль­ных ней­ро­нов в сло­ях, а так­же чис­ло сло­ёв ней­ро­нов вы­би­ра­ют­ся ис­хо­дя из спе­ци­фи­ки ре­шае­мых за­дач и тре­буе­мо­го ка­че­ст­ва ре­ше­ния. Н. с. в про­цес­се на­строй­ки на ре­ше­ние кон­крет­ной за­да­чи рас­смат­ри­ва­ет­ся как мно­го­мер­ная не­ли­ней­ная сис­те­ма, ко­то­рая в ите­ра­ци­он­ном ре­жи­ме це­ле­на­прав­лен­но ищет оп­ти­мум не­ко­то­ро­го функ­цио­на­ла, ко­ли­че­ст­вен­но оп­ре­де­ляю­ще­го ка­че­ст­во ре­ше­ния по­став­лен­ной за­да­чи. Для Н. с., как мно­го­мер­ных не­ли­ней­ных объ­ек­тов управ­ле­ния, фор­ми­ру­ют­ся ал­го­рит­мы на­строй­ки мно­жест­ва ве­со­вых ко­эф­фи­ци­ен­тов. Осн. эта­пы ис­сле­до­ва­ния Н. с. и по­строе­ния ал­го­рит­мов на­строй­ки (адап­та­ции) их ве­со­вых ко­эф­фи­ци­ен­тов вклю­ча­ют: ис­сле­до­ва­ние ха­рак­те­ри­стик вход­но­го сиг­на­ла для разл. ре­жи­мов ра­бо­ты Н. с. (вход­ным сиг­на­лом Н. с. яв­ля­ет­ся, как пра­ви­ло, вход­ная об­ра­ба­ты­вае­мая ин­фор­ма­ция и ука­за­ние т. н. учи­те­ля ней­рон­ной се­ти); вы­бор кри­те­ри­ев оп­ти­ми­за­ции (при ве­ро­ят­но­ст­ной мо­де­ли внеш­не­го ми­ра та­ки­ми кри­те­рия­ми мо­гут быть ми­ни­мум сред­ней функ­ции рис­ка, мак­си­мум апо­сте­ри­ор­ной ве­ро­ят­но­сти, в ча­ст­но­сти при на­ли­чии ог­ра­ни­че­ний на отд. со­став­ляю­щие сред­ней функ­ции рис­ка); раз­ра­бот­ка ал­го­рит­ма по­ис­ка экс­тре­му­мов функ­цио­на­лов оп­ти­ми­за­ции (напр., для реа­ли­за­ции ал­го­рит­мов по­ис­ка ло­каль­ных и гло­баль­но­го экс­тре­му­мов); по­строе­ние ал­го­рит­мов адап­та­ции ко­эф­фи­ци­ен­тов Н. с.; ана­лиз на­дёж­но­сти и ме­то­дов ди­аг­но­сти­ки Н. с. и др.

Дос­то­ин­ст­ва­ми Н. с. яв­ля­ют­ся: свой­ст­во т. н. по­сте­пен­ной де­гра­да­ции – при вы­хо­де из строя отд. эле­мен­тов ка­че­ст­во ра­бо­ты сис­те­мы па­да­ет по­сте­пен­но (для срав­не­ния, ло­гич. се­ти из эле­мен­тов И, ИЛИ, НЕ вы­хо­дят из строя при на­ру­ше­нии ра­бо­ты лю­бо­го эле­мен­та се­ти); по­вы­шен­ная ус­той­чи­вость к из­ме­не­нию па­ра­мет­ров схем, их реа­ли­зую­щих (напр., весь­ма зна­чит. из­ме­не­ния ве­со­вых ко­эф­фи­ци­ен­тов не при­во­дят к ошиб­кам в реа­ли­за­ции про­стой ло­гич. функ­ции двух пе­ре­мен­ных) и др.

Ши­ро­кое рас­про­стра­не­ние ней­ро­се­те­вых ал­го­рит­мов в об­лас­ти слож­ных фор­ма­ли­зуе­мых, сла­бо­фор­ма­ли­зуе­мых и не­фор­ма­ли­зуе­мых за­дач при­ве­ло к соз­да­нию но­во­го на­прав­ле­ния в вы­чис­лит. ма­те­ма­ти­ке – ней­ро­ма­те­ма­ти­ки. Ней­ро­ма­те­ма­ти­ка вклю­ча­ет ней­ро­се­те­вые ал­го­рит­мы ре­ше­ния сле­дую­щих за­дач: рас­по­зна­ва­ние об­ра­зов; оп­ти­ми­за­ция и экс­т­ра­по­ля­ция функ­ций; тео­рия гра­фов; крип­то­гра­фич. за­да­чи; ре­ше­ние ве­ще­ст­вен­ных и бу­лев­ских сис­тем ли­ней­ных и не­ли­ней­ных урав­не­ний; обык­но­вен­ных од­но­мер­ных и мно­го­мер­ных диф­фе­рен­ци­аль­ных урав­не­ний; диф­фе­рен­ци­аль­ных урав­не­ний в ча­ст­ных про­из­вод­ных и др.

На ос­но­ве тео­рии Н. с. соз­дан но­вый раз­дел совр. тео­рии управ­ле­ния слож­ны­ми не­ли­ней­ны­ми и мно­го­мер­ны­ми, мно­го­связ­ны­ми ди­на­мич. сис­те­ма­ми, вклю­чаю­щий ме­то­ды ней­ро­се­те­вой иден­ти­фи­ка­ции слож­ных ди­на­мич. объ­ек­тов; по­строе­ние ней­ро­ре­гу­ля­то­ров в кон­ту­рах управ­ле­ния слож­ны­ми ди­на­мич. объ­ек­та­ми и др.