МОМЕ́НТ СОПРОТИВЛЕ́НИЯ

МОМЕ́НТ СОПРОТИВЛЕ́НИЯ, гео­мет­рич. ха­рак­те­ри­сти­ка по­пе­реч­но­го се­че­ния бру­са, оп­ре­де­ляю­щая за­ви­си­мость наи­боль­ших нор­маль­ных (при из­ги­бе) или ка­са­тель­ных (при кру­че­нии) на­пря­же­ний в се­че­нии от ве­ли­чи­ны из­ги­баю­ще­го или кру­тя­ще­го мо­мен­тов. Раз­ли­ча­ют М. с. осе­вой (при из­ги­бе) и по­ляр­ный (при кру­че­нии).

Осе­вым М. с. на­зы­ва­ет­ся от­но­ше­ние мо­мен­та инер­ции от­но­си­тель­но дан­ной цен­траль­ной оси к рас­стоя­нию от этой оси до наи­бо­лее уда­лён­ной точ­ки по­переч­но­го се­че­ния: $W_x=\frac{I_x}{Y_{\text {макс}}}, W_y=\frac{I_y}{X_{\text {макс}}}$.

По­ляр­ным М. с. на­зы­ва­ет­ся от­но­ше­ние по­ляр­но­го мо­мен­та инер­ции к рас­стоя­нию от по­лю­са, рас­по­ло­жен­но­го в цен­тре тя­же­сти по­пе­реч­но­го се­че­ния, до наи­бо­лее уда­лён­ной точ­ки се­че­ния: $W_{\text p}=\frac{I_{\text p}}{\rho_{\text {макс}}}$. Раз­мер­ность М. с. – м³.

При рас­чё­те на проч­ность бру­са макс. нор­маль­ные (при из­ги­бе) и ка­са­тель­ные (при кру­че­нии) на­пря­же­ния вычис­ля­ют­ся по фор­му­лам: $\sigma_{\text {макс}}=\frac{M_{\text {изг}}}{W_x}, \tau_{\text {макс}}=\frac{M_{\text {кр}}}{W_р}$. Для круг­ло­го се­че­ния радиу­са $R$ име­ем $W_x=\frac{\pi R^3}{4}$ и $W_{\text p}=\frac{\pi R^3}{2}$; для пря­мо­уголь­но­го се­че­ния со сто­ро­на­ми $b$ (па­рал­лель­ной гл. оси) и $h$ (перпен­ди­ку­ляр­ной ей) – 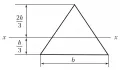$W_x=\frac{bh^2}{6}$. Ес­ли по­пе­реч­ное се­че­ние бру­са не сим­мет­рич­но от­но­си­тель­но оси из­ги­ба, а ма­те­ри­ал име­ет раз­ные пре­де­лы проч­но­сти на рас­тя­же­ние и сжа­тие, то не­об­хо­ди­мо оп­ре­де­лять на­пря­же­ния по обо­им кра­ям бру­са и со­от­вет­ст­вен­но вы­чис­лять два мо­мен­та со­про­тив­ле­ния. Напр., для бруса тре­уголь­но­го се­че­ния (рис.) мо­мент инерции $I_x=\frac{bh^3}{36}$. М. с. от­но­си­тель­но нижних во­ло­кон $W_{x \text н}=\frac {I_x}{\frac{h}{3}}=\frac{bh^2}{12}$, верх­них – $W_{x \text в}=\frac {I_x}{\frac{2h}{3}}=\frac{bh^2}{24}$.