МЕМБРА́НА

МЕМБРА́НА (лат. membrana – ко­жи­ца, пе­ре­пон­ка), гиб­кая тон­кая плён­ка, при­ве­дён­ная внеш­ни­ми си­ла­ми в со­стоя­ние на­тя­же­ния и об­ла­даю­щая вслед­ст­вие это­го уп­ру­го­стью. В ме­ха­ни­ке М. на­зы­ва­ют тон­кую пла­сти­ну с ис­че­заю­ще ма­лой жё­ст­ко­стью на из­гиб. Уп­ру­гие свой­ст­ва М. не за­ви­сят от ма­те­риа­ла и тол­щи­ны. М. от­но­сит­ся к дву­мер­ным ко­ле­ба­тель­ным сис­те­мам с рас­пре­де­лён­ны­ми па­ра­мет­ра­ми. М. мож­но толь­ко рас­тя­ги­вать, но не сжи­мать, т. к. от­сут­ст­вие из­гиб­ной жё­ст­ко­сти при­во­дит к по­те­ре ус­той­чи­во­сти при по­яв­ле­нии сжи­маю­щих уси­лий. Си­лы, рас­тя­ги­ваю­щие М., все­гда на­прав­ле­ны по ка­са­тель­ной к её по­верх­но­сти, по­это­му М. обыч­но за­кре­п­ле­на по внеш­не­му кон­ту­ру. При­ме­ра­ми М. яв­ля­ют­ся ко­жа, на­тя­ну­тая на ба­ра­бан, тон­кая ме­тал­лич. фоль­га, иг­раю­щая роль под­виж­ной об­клад­ки кон­ден­са­тор­но­го мик­ро­фо­на, и др. В строи­тель­ст­ве мем­бран­ные кон­ст­рук­ции из тон­ких ме­тал­лич. лис­тов ши­ро­ко при­ме­ня­ют­ся для по­кры­тий боль­ше­про­лёт­ных со­ору­же­ний (кры­тых ста­дио­нов, вы­ста­воч­ных па­виль­о­нов, кон­церт­ных за­лов и др.).

Рис. 1. Форма первых четырёх собственных колебаний прямоугольной мембраны; стрелками указаны узловые линии.

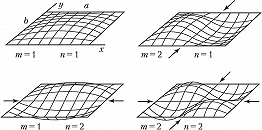
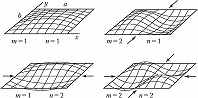
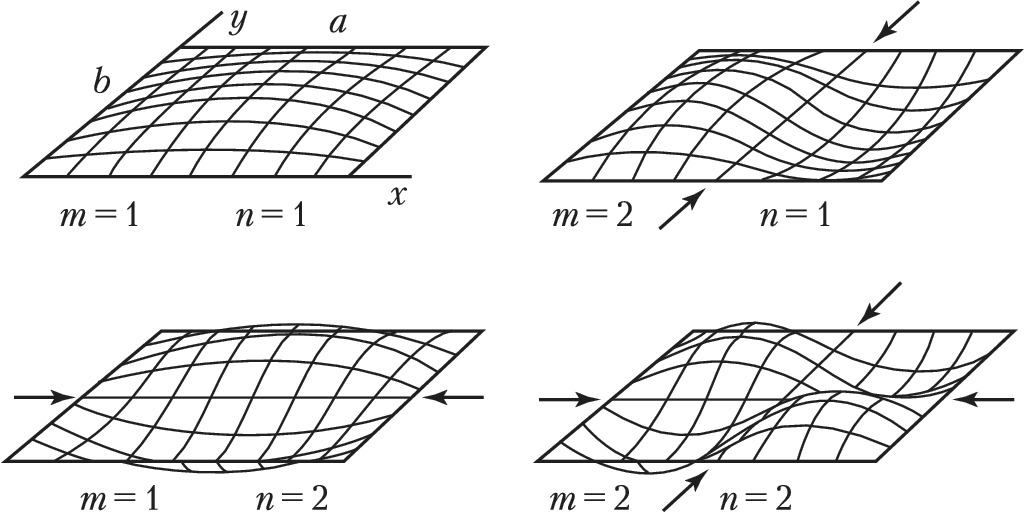
Ма­лые по­пе­реч­ные ко­ле­ба­ния од­но­род­ной, рав­но­мер­но рас­тя­ну­той М. в пре­неб­ре­же­нии рас­сея­ни­ем энер­гии опи­сы­ва­ют­ся урав­не­ни­ем Д’Аламбера. Соб­ст­вен­ные (сво­бод­ные) ко­ле­ба­ния М. представ­ля­ют со­бой стоя­чие вол­ны. Уча­ст­ки М., ко­леб­лю­щие­ся с про­ти­во­по­лож­ны­ми фа­за­ми, раз­де­ля­ют­ся уз­ло­вы­ми ли­ния­ми, на ко­то­рых ам­пли­ту­ды ко­ле­ба­ний рав­ны ну­лю. Собств. час­то­ты ко­ле­ба­ний М. об­ра­зу­ют дис­крет­ный спектр. Для пря­мо­уголь­ной М. со сто­ро­на­ми $а$ и $b$ (рис. 1) собств. час­то­ты опи­сы­ва­ют­ся фор­му­лой

$\omega _{nm}=\pi c\sqrt{n^2/a^2+m^2/b^2}$ $(n, m=1, 2, 3,…),$

Рис. 2. Положения узловых линий в квадратной мембранепри и различных соотношениях между амплитудами u12 и u21.

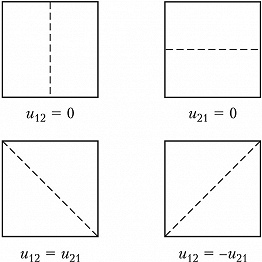
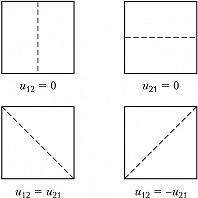
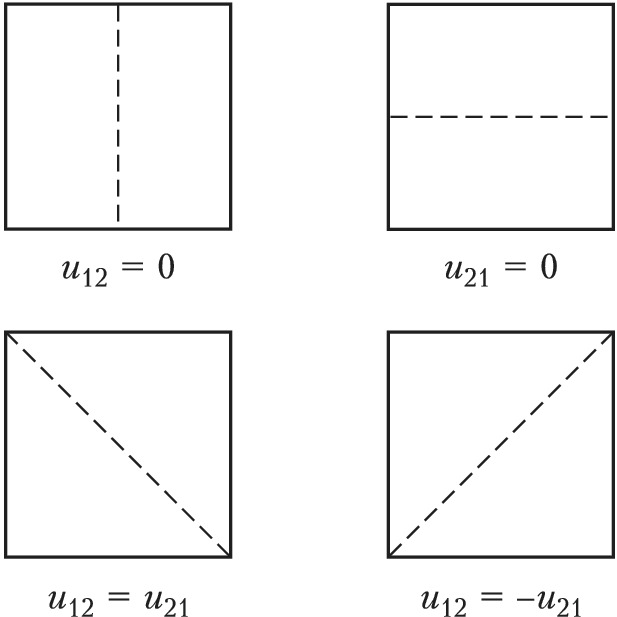
где  $c=\sqrt{T/\rho }$ – ско­рость рас­про­стра­не­ния ко­ле­ба­ний ($T$ – на­тя­же­ние, $ρ$ – по­верх­но­ст­ная плот­ность М.). Час­то­та $ω_{11}$ яв­ля­ет­ся ос­нов­ной (наи­бо­лее низ­кой), обер­то­ны $ω_{𝑘𝑘}=𝑘ω_{11}$ ($𝑘$=2, 3,…) пред­став­ля­ют со­бой гар­мо­ни­ки осн. час­то­ты. Од­ной и той же час­то­те мо­гут со­от­вет­ство­вать неск. форм ко­ле­ба­ний с разл. по­ло­же­ни­ем уз­ло­вых ли­ний. Напр., в квад­рат­ной мем­бра­не ($b = a$) две фор­мы собств. ко­ле­ба­ний $u_{12}$ и $u_{21}$ име­ют од­ну и ту же час­то­ту, а их уз­ло­вые ли­нии в те­че­ние пе­рио­да по­сле­до­ва­тель­но при­ни­ма­ют разл. кон­фи­гу­ра­ции (рис. 2).

Собств. час­то­ты ко­ле­ба­ний круг­лой М. опи­сы­ва­ют­ся с по­мо­щью функ­ций Бес­се­ля, и ни один из обер­то­нов не яв­ля­ет­ся гар­мо­ни­кой осн. час­то­ты.

Вы­ну­ж­ден­ные ко­ле­ба­ния М. про­ис­хо­дят с час­то­той внеш­не­го воз­дей­ст­вия, при сов­па­де­нии ко­то­рой с од­ной из собств. час­тот име­ет ме­сто ре­зо­нанс. Раз­ли­ча­ют ки­не­ма­тич. и си­ло­вой спо­со­бы воз­бу­ж­де­ния вы­ну­ж­ден­ных ко­ле­ба­ний. При этом точ­ка (об­ласть) при­ло­же­ния внеш­ней си­лы не долж­на сов­па­дать с ли­ни­ей уз­лов.

М. пред­став­ля­ет со­бой из­лу­ча­тель зву­ка с не­рав­но­мер­ным рас­пре­де­ле­ни­ем ко­ле­ба­тель­ной ско­ро­сти по по­верх­но­сти, по­это­му из­лу­че­ние М., воз­бу­ж­дён­ной на осн. час­то­те, не об­ла­да­ет боль­шой на­прав­лен­но­стью.