КИНЕМА́ТИКА МЕХАНИ́ЗМОВ
-
Рубрика: Технологии и техника
-
-
Скопировать библиографическую ссылку:
КИНЕМА́ТИКА МЕХАНИ́ЗМОВ, раздел теории механизмов и машин, в котором изучают движение звеньев механизма без учёта вызывающих его причин. Осн. задачи кинематич. анализа механизмов – определение положения звеньев и траекторий отд. точек, их линейных скоростей и ускорений, угловых скоростей и ускорений звеньев. Кинематич. анализ механизмов основывается на том, что при заданном движении одного или нескольких звеньев, число которых равно числу степеней свободы, остальные звенья движутся по определённому закону, обусловленному структурой (строением) механизма. Для решения задач К. м. создаётся кинематич. схема механизма, на которой указаны кинематические пары и размеры звеньев, определяющие их взаимное расположение. По кинематич. схеме определяется число степеней свободы механизма и задаётся закон движения ведущих (начальных) звеньев, т. н. закон изменения обобщённых координат. Задачи К. м. решаются графическими и аналитич. методами.
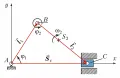
Наиболее простым является графич. метод определения положения звеньев плоского механизма, напр. кривошипно-ползунного (рис.), при котором проводятся определённые построения. Положение звена $AB$ (кривошип) определяется обобщённой координатой $\phi_1$; при соответствующем угле поворота звена $AB$ (цикл поворота) определяется положение остальных звеньев. Для изучения характера возвратно-поступат. движения механизма применяется аналитич. метод, который требует дополнит. рассмотрения функциональной зависимости изменения угла $\phi_2$ и координат любой точки на звеньях (напр., точки $S_2$) от угла $\phi_1$ при его изменении. Для пространственных механизмов графич. построения усложняются, т. к. они связаны с определением линий пространственных фигур и точек их пересечения.
При определении скоростей и ускорений звеньев применяются следующие методы: графический, при котором используют построение кинематич. диаграмм и планов скоростей и ускорений; аналитич. метод векторных контуров, преобразования координат и др. При применении метода кинематич. диаграмм строится графич. зависимость перемещения к.-л. точки механизма во времени, которую можно получить при построении схемы механизма для разл. положений ведущего звена за один оборот. Применяя графич. дифференцирование, строят диаграмму изменения скорости и ускорения. Метод даёт наглядное представление об изменении кинематич. параметров, однако отличается небольшой точностью, особенно при построении диаграммы изменения ускорения.
При решении задачи об определении скоростей и ускорений используют соотношения, устанавливающие зависимости между скоростями и ускорениями в векторной форме. Численные значения скоростей и ускорений определяются в результате решения векторных уравнений графич. методом. При кинематич. анализе механизма за полный цикл движения строят планы скоростей и ускорений для ряда положений кривошипа $AB$ при повороте его на 360° с постоянной угловой скоростью.
Графич. методы обладают наглядностью и универсальностью, но не обеспечивают достаточную точность. В ряде случаев предпочтительнее использовать аналитич. методы, позволяющие с любой степенью точности определять кинематич. параметры и выявлять их взаимосвязь с размерами звеньев механизма. В этом случае удобнее применять метод векторных контуров, представляя звенья в виде векторов $\boldsymbol l_1$ и $\boldsymbol l_2$, определяющих вместе с вектором $\boldsymbol S_c$ положение точки $C$ на оси $x$ и образующих замкнутый контур, векторное уравнение которого имеет вид: $\boldsymbol S_c=\boldsymbol l_1+\boldsymbol l_2$. Проектируя векторы этого уравнения на оси координат $x$ и $y$, получают аналитич. зависимости (систему уравнений), из которых определяют функцию положения $\phi_2=\phi_2(\phi_1)$, а после дифференцирования – скорость и ускорение звена $C$, угловую скорость и ускорение звена $BC$. При использовании аналитич. методов наиболее трудной является задача об определении положения звеньев, т. к. она сводится в общем случае к решению нелинейных уравнений, в отличие от задачи об определении скоростей и ускорений, которая всегда может быть сведена к решению линейных уравнений.
Кинематич. анализ пространственных механизмов целесообразно выполнять методом преобразования координат, при котором с каждым звеном механизма связывается прямоугольная система координат. Метод требует использования матричной формы записи уравнений преобразования координат, связан с большим объёмом вычислений, поэтому решения выполняются на ЭВМ.
Кинематич. анализ применяется при проектировании зубчатых, кулачковых и др. механизмов. При этом используются методы, учитывающие особенности конструкции. В некоторых случаях существенным является синтез механизмов, напр. когда требуется нахождение размеров, определяющих кинематич. схему по заданным положениям, скоростям и ускорениям звеньев и отд. точек.
