АНОМА́ЛИИ

АНОМА́ЛИИ в не­бес­ной ме­ха­ни­ке, ве­ли­чи­ны, оп­ре­де­ляю­щие по­ло­же­ние не­бес­но­го те­ла (пла­не­ты, спут­ни­ка и т. п.) на эл­лип­тич. ор­би­те. Раз­ли­ча­ют А. ис­тин­ную, экс­цен­три­че­скую и сред­нюю.

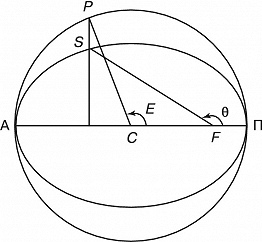
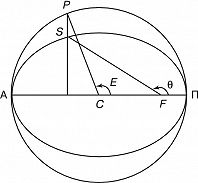
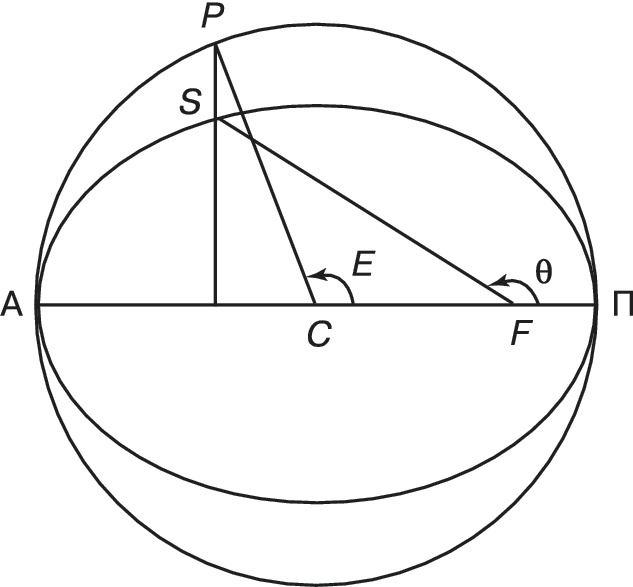
Ис­тин­ная А. – угол $θ$ с вер­ши­ной в фо­ку­се ор­би­ты $F$ ме­ж­ду на­прав­ле­ни­ем на пе­ри­центр $\text Π$ (пе­ри­гей, пе­ри­ге­лий) ор­би­ты и ра­диу­сом-век­то­ром не­бес­но­го те­ла $S$ (рис.); от­счи­ты­ва­ет­ся в на­прав­ле­нии дви­же­ния те­ла.

Экс­цен­трическая А. – угол $E$ с вер­ши­ной в цен­тре ор­би­ты $C$ ме­ж­ду на­прав­ле­ния­ми на пе­ри­центр $\text Π$ и на фик­тив­ную точ­ку $P$, смысл ко­то­рой ясен из ри­сун­ка.

Сред­няя А. – угол $M$ с вер­ши­ной в цен­тре ор­би­ты $C$ ме­ж­ду на­прав­ле­ния­ми на пе­ри­центр $\text Π$ и на не­ко­то­рую фик­тив­ную точ­ку $L$ (угол $M$ и точка $L$ не по­ка­заны на рис.), ко­то­рая дви­жет­ся по ок­руж­но­сти $\text ΠP\text Α$ рав­но­мер­но и про­хо­дит че­рез пе­ри­центр и апо­центр $\text Α$ од­но­вре­мен­но с не­бес­ным те­лом $S$.

В со­от­вет­ст­вии со 2-м за­ко­ном Ке­п­лера ис­тин­ная и экс­цен­трич. А. из­ме­ня­ют­ся не­рав­но­мер­но: бы­ст­рее, ко­гда не­бес­ное те­ло дви­жет­ся вбли­зи пе­ри­цен­тра, и мед­лен­нее – вбли­зи апо­цен­тра. При дви­же­нии не­бес­но­го те­ла $S$ от $\text Π$ до $\text Α$ оно опе­ре­жа­ет фик­тив­ную точ­ку $L (θ>E>M)$, а за­тем, при дви­же­нии от $\text Α$ до $\text Π$, от­ста­ёт от неё $(θ{<}E{<}М)$. В мо­мен­ты про­хо­ж­де­ния те­ла че­рез точ­ки $\text Π$ и $\text Α$ все три А. сов­па­да­ют.

Сред­няя А. в мо­мент вре­ме­ни $t$ оп­ре­де­ля­ет­ся со­от­но­ше­ни­ем: $$M=\frac{2\pi}{T}(t-τ),$$ где $τ$ – мо­мент про­хо­ж­де­ния пе­ри­цен­тра, $T$ – пе­ри­од об­ра­ще­ния.

Экс­цен­трич. А. свя­за­на со сред­ней А. урав­не­ни­ем Ке­п­ле­ра: $E-e{\sin} {E}=M$, где $e$ – экс­цен­три­си­тет ор­би­ты.

Ис­тин­ная А. на­хо­дит­ся ре­ше­ни­ем урав­не­ния $$\text {tg}\frac{θ}{2}=\sqrt{\frac{1+e}{1-e}} \text {tg} \frac E2.$$

.

На ги­пер­бо­лич. и па­ра­бо­лич. ор­би­тах оп­ре­де­ле­на ис­тин­ная А., а экс­цен­три­че­скую и сред­нюю А. сле­ду­ет за­ме­нить их ана­ло­га­ми для со­от­вет­ст­вую­щих ор­бит.