ФЕ́ЙНМАНА ДИАГРА́ММЫ

ФЕ́ЙНМАНА ДИАГРА́ММЫ, гра­фич. изо­бра­же­ние про­цес­сов рас­про­стра­не­ния и взаи­мо­дей­ст­вия эле­мен­тар­ных час­тиц в кван­то­вой тео­рии. Вве­де­ны Р. Фейн­ма­ном (1949) для опи­са­ния рас­сея­ния, вза­им­но­го пре­вра­ще­ния час­тиц и вы­чис­ле­ния ам­пли­туд ве­ро­ят­но­стей в кван­то­вой элек­тро­ди­на­ми­ке. Ме­тод диа­грамм­ной тех­ни­ки сыг­рал важ­ней­шую роль в раз­ви­тии кван­то­вой тео­рии по­ля (КТП); он так­же ши­ро­ко ис­поль­зу­ет­ся в ста­ти­стич. фи­зи­ке и тео­рии твёр­до­го те­ла.

Рис. 1. Элементы диаграмм Фейнмана в квантовой электродинамике: а – распространение фотона; б – распространение электрона; в – вершина испускания (поглощения) фотона электроном.

Рис. 2. Диаграммы Фейнмана, соответствующие процессам комптоновского рассеяния (а), мёллеровского рассеяния (упругого рассеяния электрона на электроне) (б) и аннигиляции (в).

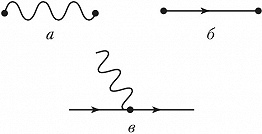
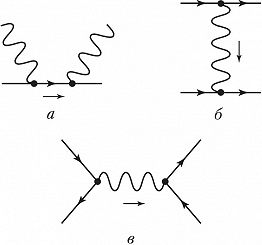
Эле­мен­та­ми диа­грамм­ной тех­ни­ки яв­ля­ют­ся вер­ши­ны (точ­ки), внутр. и внеш­ние ли­нии, пет­ли (замк­ну­тые цик­лы). Так, час­ти­ца, рас­про­стра­няю­щая­ся из од­ной точ­ки в дру­гую, изо­бра­жа­ет­ся ли­ни­ей, со­еди­няю­щей эти точ­ки. Эле­мен­тар­ным ак­том взаи­мо­дей­ст­вия в КТП яв­ля­ет­ся ис­пус­ка­ние и по­гло­ще­ние час­тиц разл. сор­та. Напр., элек­тро­маг­нит­ное взаи­мо­дей­ст­вие сво­дит­ся к ис­пус­ка­нию и по­гло­ще­нию за­ря­жен­ной час­ти­цей кван­та элек­тро­маг­нит­но­го по­ля – фо­то­на. Гра­фи­че­ски это­му со­от­вет­ст­ву­ет вер­шин­ная диа­грам­ма, где пря­мые ли­нии обо­зна­ча­ют элек­трон, вол­ни­стые – фо­тон (рис. 1). С по­мо­щью при­ве­дён­ных эле­мен­тов диа­грамм мож­но по­стро­ить Ф. д. лю­бо­го про­цес­са в кван­то­вой элек­тро­ди­на­ми­ке. Напр., пред­став­лен­ные на рис. 2 Ф. д. опи­сы­ва­ют про­цес­сы рас­сея­ния и ан­ни­ги­ля­ции в ве­ду­щем по­ряд­ке тео­рии воз­му­ще­ний по кон­стан­те элек­тро­маг­нит­но­го взаи­мо­дей­ст­вия α=е²/(hc)≈¹/₁₃₇ (е – элек­трич. за­ряд элек­тро­на, h – по­сто­ян­ная План­ка, с – ско­рость све­та). Внеш­ние ли­нии изо­бра­жа­ют сво­бод­ные час­ти­цы до и по­сле столк­но­ве­ния, а внут­рен­ние – дви­же­ние час­ти­цы в вир­ту­аль­ном со­стоя­нии. Од­на и та же внеш­няя ли­ния мо­жет изо­бра­жать как на­чаль­ную час­ти­цу, так и ко­неч­ную ан­ти­час­ти­цу. По т. н. пра­ви­лам Фейн­ма­на ка­ж­до­му эле­мен­ту диа­грам­мы со­пос­тав­ля­ет­ся оп­ре­де­лён­ное ма­те­ма­тич. вы­ра­же­ние. Пра­ви­ла Фейн­ма­на мо­гут быть сфор­му­ли­ро­ва­ны как в ко­ор­ди­нат­ном, так и в им­пульс­ном пред­став­ле­нии, т. е. со­от­вет­ст­во­вать про­цес­су, про­ис­хо­дя­ще­му в оп­ре­де­лён­ных точ­ках про­стран­ст­ва-вре­ме­ни или с час­ти­ца­ми, не­су­щи­ми оп­ре­де­лён­ный им­пульс.

Рис. 3. Диаграммы Фейнмана, соответствующие процессу комптоновского рассеяния (а) и радиационные поправки за счёт испускания виртуальных (б, в) и реального (г) фотонов.

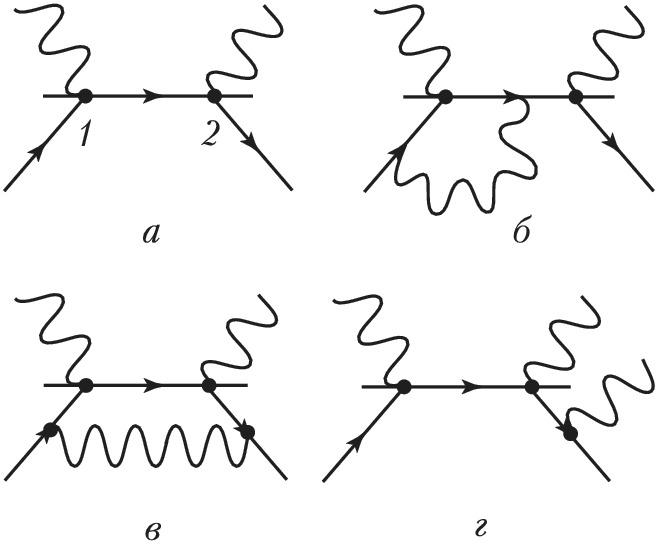
Для вы­чис­ле­ния ве­ро­ят­но­сти к.-л. про­цес­са не­об­хо­ди­мо най­ти ам­пли­ту­ду ве­ро­ят­но­сти, ко­то­рая изо­бра­жа­ет­ся со­от­вет­ст­вую­щей Ф. д. с за­дан­ны­ми на­чаль­ны­ми и ко­неч­ны­ми час­ти­ца­ми. Ко­ли­че­ст­во вер­шин в Ф. д. оп­ре­де­ля­ет по­ря­док тео­рии воз­му­ще­ний по ма­ло­му па­ра­мет­ру (кон­стан­те взаи­мо­дей­ст­вия). В низ­шем по­ряд­ке, как пра­ви­ло, при­сут­ст­ву­ют диа­грам­мы без пе­тель, на­зы­вае­мые дре­вес­ны­ми диа­грам­ма­ми. В сле­дую­щих по­ряд­ках, на­зы­вае­мых ра­диа­ци­он­ны­ми по­прав­ка­ми, при­сут­ст­ву­ют диа­грам­мы с пет­ля­ми (рис. 3). В этом слу­чае про­ис­хо­дит ин­тег­ри­ро­ва­ние по че­ты­рёх­мер­но­му им­пуль­су вир­ту­аль­ных час­тиц внут­ри пет­ли.

Ка­ж­дую Ф. д. мож­но ин­тер­пре­ти­ро­вать по-раз­но­му в за­ви­си­мо­сти от на­прав­ле­ния дви­же­ния вдоль ли­ний диа­грам­мы. Так, напр., для диа­грам­мы а на рис. 3 при дви­же­нии сле­ва на­пра­во – это рас­сея­ние фо­то­на на элек­тро­не: на­чаль­ный элек­трон по­гло­ща­ет фо­тон в вер­ши­не 1, об­ра­зу­ет­ся про­ме­жу­точ­ный элек­трон, ко­то­рый дви­жет­ся от вер­ши­ны 1 к вер­ши­не 2, где он из­лу­ча­ет ко­неч­ный фо­тон и пре­вра­ща­ет­ся в ко­неч­ный элек­трон. При рас­смат­ри­ва­нии дви­же­ния сни­зу вверх Ф. д. пред­став­ля­ет про­цесс ан­ни­ги­ля­ции элек­тро­на (сле­ва) и по­зи­тро­на (спра­ва) и пре­вра­ще­ние их в два фо­то­на.

Ф. д. мож­но по­стро­ить и для др. ви­дов взаи­мо­дей­ст­вий, ис­хо­дя из со­от­вет­ст­вую­ще­го ла­гран­жиа­на. Ко­ли­че­ст­во Ф. д. в ка­ж­дом по­ряд­ке тео­рии воз­му­ще­ний рас­тёт как фак­то­ри­ал, что оп­ре­де­ля­ет асим­пто­тич. ха­рак­тер по­лу­чае­мых раз­ло­же­ний.

Лит.: Би­лень­кий С. М. Вве­де­ние в диа­грамм­ную тех­ни­ку Фейн­ма­на. М., 1971; Фейн­ман Р. Тео­рия фун­да­мен­таль­ных про­цес­сов. М., 1978.

Д. И. Ка­за­ков.