Циклотро́нно-фоно́нный резона́нс, резонансное поглощение электромагнитной энергии, обусловленное переходами электронов между уровнями Ландау при участии оптических фононов. Наблюдается при распространении электромагнитных волн в полупроводнике, находящемся в постоянном магнитном поле напряжённостью ${\boldsymbol H}$. Для возникновения циклотронно-фононного резонанса необходимо достаточно сильное (квантующее) магнитное поле ${H > m^{*}c\boldsymbol{k}T/|e|\hbar}$ (${m^{*}}$ и ${e}$ – эффективная масса и заряд электрона, ${c}$ – скорость света, $\hbar$ – постоянная Планка, $\boldsymbol{k}$ – постоянная Больцмана, ${T}$ – температура) и оптические ветви в колебательном спектре полупроводника (см. Динамика кристаллической решётки).

В квантующем магнитном поле электроны имеют непрерывный энергетический спектр для движения вдоль поля и дискретный – для поперечного движения. Если зависимость энергии ${ℰ}$ электрона от его квазиимпульса $\boldsymbol{p}$ изотропна и квадратична, то энергия электрона определяется соотношением:

$${ℰ_n(p_H)=(n+1/2)\hbar ω_c+p_{H^2}/2m}, \tag{1}$$где ${n}$ – целое положительное число, $\textit{р}_{H}$ – компонента квазиимпульса в направлении ${\boldsymbol H}$, ${ω_c=|e|\boldsymbol{H}/mc}$ – циклотронная частота электрона. Условие ${ℰ_n-ℰ_{n–1} = \hbarω}$ где $\omega$ – частота внешнего электромагнитного поля, $\boldsymbol{p}_{H}$ фиксировано) приводит к циклотронному резонансу. Однако при условии, что расстояние между уровнями Ландау совпадает с суммой или разностью энергий оптического фонона и фотона, в поглощении электромагнитной энергии также наблюдается резонанс на частоте $\omega$ (см. рисунок).

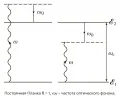Электронные переходы с участием оптического фонона.Электронные переходы с участием оптического фонона.Циклотронно-фононный резонанс обусловлен перебросом электронов между уровнями Ландау за счёт взаимодействия электронов с оптическими фононами и фотонами. В отсутствие фотона циклотронно-фононный резонанс переходит в магнитофононный резонанс. Коэффициент поглощения электромагнитной энергии при циклотронно-фононном резонансе зависит от характера поляризации электромагнитной волны. Циклотронно-фононный резонанс имеет место, если вектор напряжённости электрического поля волны ${\boldsymbol E⊥ \boldsymbol H}$, в противном случае циклотронно-фононный резонанс отсутствует.

Если хотя бы один из размеров образца ${d}$ достаточно мал (например, образец – тонкая плёнка), то возникает дополнительное размерное квантование спектра (см. Размерные эффекты). Если ось ${Oz}$ направлена вдоль толщины плёнки ${d}$, то дискретизация электронного спектра в этом направлении приводит к т. н. размерно-фононному резонансу, связанному с переходом электрона между уровнями размерно-квантованного спектра за счёт поглощения оптического фонона и фотона. Если вдоль оси ${Oz}$ приложить квантующее поле ${\boldsymbol H}$, то электронный спектр становится полностью дискретным и кроме линий циклотронно-фононного резонанса и размерно-фононного резонанса возникают новые серии линий размерно-циклотронно-фононного резонанса.

Наряду с обычным циклотронно-фононным резонансом, наблюдаются циклотронно-фононный резонанс, сопровождающийся переворотом спина электрона, и многофононный циклотронно-фононный резонанс.