ТА́ЛЬБОТА ЭФФЕ́КТ

ТА́ЛЬБОТА ЭФФЕ́КТ (Таль­бо эф­фект), са­мо­вос­про­из­ве­де­ние све­то­во­го по­ля с пе­рио­дич. мо­ду­ля­ци­ей ам­пли­ту­ды при рас­про­стра­не­нии в ли­ней­ной сре­де. Об­на­ру­жен для све­то­во­го по­ля с про­стран­ст­вен­но-пе­рио­дич. мо­ду­ля­ци­ей в 1836 У. Г. Ф. Таль­ботом (Тол­бо­том). Ис­сле­до­ван в 1881 Дж. Рэ­ле­ем, по­ка­зав­шим, что Т. э. яв­ля­ет­ся след­ст­ви­ем ди­фрак­ции Фре­не­ля.

Самовоспроизведение распределения амплитуды волны (транспарант) на экране.

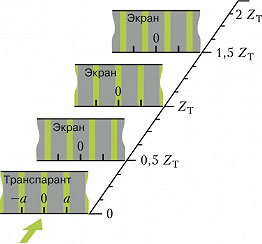
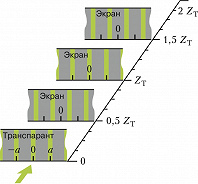
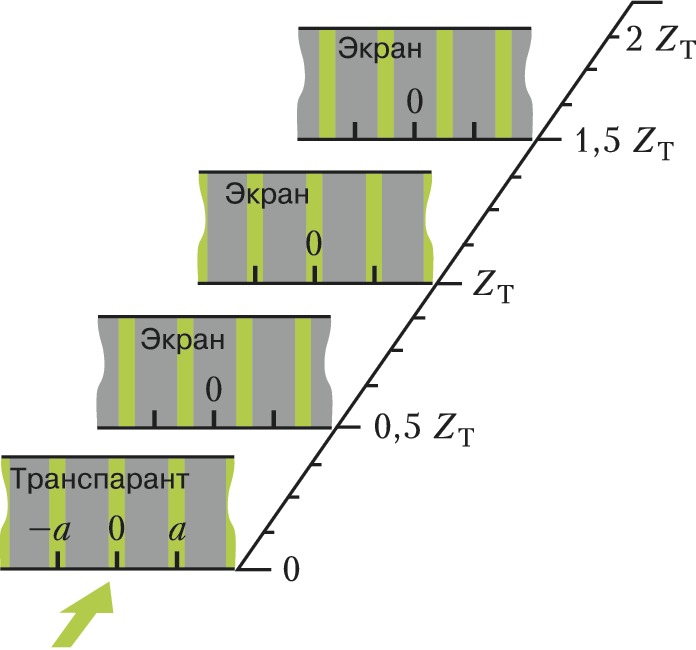
При па­де­нии пло­ской вол­ны с ам­пли­ту­дой $A(x)$ на пе­рио­дич. ди­фрак­ци­он­ную ре­шёт­ку с пе­рио­дом $a$ (транс­па­рант, на ко­то­ром при­ве­де­но рас­пре­де­ле­ние ам­пли­ту­ды вол­ны, рис.) об­раз вол­ны по­вто­ря­ет­ся че­рез рав­ные рас­стоя­ния от плос­ко­сти ре­шёт­ки. Рас­стоя­ние, на ко­то­ром вос­про­из­во­дит­ся точ­ное изо­бра­же­ние вол­ны, рав­но $Z_T= 2a^2/λ$, т. н. рас­стоя­ние Таль­бо­та ($λ$ – дли­на вол­ны). На этом рас­стоя­нии все гар­мо­ни­ки дис­крет­но­го спек­тра ам­пли­ту­ды $A(x)$ при ди­фрак­ции све­то­во­го по­ля на про­стран­ст­вен­ной ре­шёт­ке при­об­ре­та­ют на­бег фа­зы, крат­ный $2π$, вслед­ст­вие че­го про­ис­хо­дит точ­ное вос­про­из­ве­де­ние ис­ход­ной вол­ны. Вос­про­из­ве­де­ние изо­бра­же­ния, по­вто­ряю­щее­ся на рас­стоя­ни­ях $Z_T·n$, где $n=2,3$, на­зы­ва­ет­ся кратным Т. э. На рас­стоя­ни­ях, рав­ных $Z_T·(n+1/2)$, изо­бра­же­ние сдви­га­ет­ся от­но­си­тель­но пер­во­на­чаль­но­го на по­ло­ви­ну пе­рио­да. Умень­ше­ние пе­рио­да в изо­бра­же­нии на рас­стоя­нии $Z_T·(n+1/q)$, где $q=3,4,5$, на­зы­ва­ет­ся дроб­ным эф­фек­том Таль­бо­та.

При дву­мер­ной мо­ду­ля­ции ам­пли­ту­ды $A(x, y)$ Т. э. су­ще­ст­ву­ет, ес­ли со­из­ме­ри­мы квад­ра­ты пе­рио­дов мо­ду­ля­ции по осям $x$, $y$. Для све­то­во­го по­ля с мо­ду­ля­ци­ей ам­пли­ту­ды на тре­уголь­ной рав­но­сто­рон­ней ре­шёт­ке со сто­ро­ной а рас­стоя­ние Таль­бо­та рав­но $Z_T^a=(3/4)Z_T$.

Для вол­но­во­го по­ля с пе­рио­дич. мо­ду­ля­ци­ей ам­пли­ту­ды во вре­ме­ни эф­фект са­мо­вос­про­из­ве­де­ния, ана­ло­гич­ный Т. э., воз­ни­ка­ет в сре­де с квад­ра­тич­ной дис­пер­си­ей при рас­про­стра­не­нии на рас­стоя­ние $Z_T^{\text{time}}=\frac{T^2}{\pi|d^2k/dω^2|}$ где $T$ – пери­од мо­ду­ля­ции, $k=k(ω)$ – дис­пер­си­он­ное со­от­но­ше­ние для сре­ды, $ω$ – ча­с­то­та вол­ны.

Т. э. при­ме­ня­ют в ин­тер­фе­ро­мет­рич., спек­траль­ных из­ме­ре­ни­ях, для фа­зо­вой син­хро­ни­за­ции ла­зер­ных ре­шё­ток. Эф­фект са­мо­вос­про­из­ве­де­ния по­лей, мо­ду­ли­ро­ван­ных во вре­ме­ни, ис­поль­зу­ет­ся для ко­ди­ро­ва­ния ин­фор­ма­ции.